
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование функций с помощью производных. Простроение графиков функций.
§1.Условия постоянства, возрастания и убывания функций
При изучении характера изменения функции и ее графика на первом месте стоит вопрос, при каких условиях функция сохраняет в данном промежутке постоянное значение или меняется монотонно? Для простоты промежуток будем считать сегментом. Напомним, что на Ответ на вопрос дают следующие теоремы. Теорема 1. Пусть функция у=f(x) определена и непрерывна на [а,в], и на (а,в) имеет конечную производную f '(x). Для того чтобы f(x) была постоянной на [а,в], Н. и Д., чтобы f '(x)=0 на [а,в]. Доказательство. 1. Достаточность Пусть f '(x)=0 при xÎ(а,в). Возьмем произв. [а,х] где а<х£в. На [а,х] функция f(x) удовлетворяет всем условиям т-мы Лагранжа. Тогда сущ. т.c а<c<х, что f(x)-f(а)=(х-а)*f '(с). Но f '(с)=0 отсюда f(x)=f(а)= const для любого х Î(а,в). 2.Необходимость Пусть f(x)= С=const для любого х Î(а,в). Но тогда f '(x)=C '=0 на (а,в).
Теорема 2. Пусть функция у=f(x) определена и непрерывна на [а,в], и в (а,в) им. конечную произв f '(x). Для того чтобы функция f(x) была неубывающей (невозрастающей) на [а,в], Н. и Д., чтобы для всех xÎ(а,в) было f '(x)³0 ( f '(x)£0). Д-во проведем для случая неубывающей функции (для невозрастающей сам-но). 1. Достаточность Пусть f '(x)³0 на [а,в],те для люб. хÎ(а,в). Возьмем две произвольные точки  2.Необходимость. Пусть f(x) неубывает на [а,в]. Это значит , что для любых точек
Теорема 3. Пусть функция у=f(x) определена и непрерывна на [а,в] и им конечную производную f '(x) на (а,в). Для того, чтобы функция у=f(x) была возрастающей (убывающей), достаточно выпол. условия f'(x)>0 (f'(x)<0) для люб. х принад. (а,в). Доказательство для возрастания аналогичное док-ву достаточности в Т-ме 2, только нестрогое неравенство везде следует заменить на строгое >. (Для убывания аналогично). Замечание. Из т-мы 3 следует, что строгое возрастание функции вытекает из f'(x)>0. Наоборот не всегда верно: даже для строго возрастающей функции производная может обращаться в ноль. Те f'(x)³0 только. Пример: у=х3 возрастает на [-1,1], но в т. х=0 у'(0)=3х2 Вывод: касательная и к графику возрастающей функции может быть парал. оси ох. Доказанные теоремы имеют простой геометрический смысл. Т.к. f'(x) означает угловой коэффициент касательной к графику функции у=f(x) в точке с абсциссой х то в случае f'(x)>0 касат. к графику наклонена под острым углом к оси ох- кривая возрастает, в случае f'(x)<0 касат. наклонена под тупым углом к ох- кривая убывает. Если f'(x)=0 , то в точке Пример: Исследовать на монотонность ф-ю
§2.Экстремумы функций В первом пункте мы рассмотрели непрерывную на [а,в] ф-ию, явл. монотонной. Пусть теперь на [а,в] определена и непрерывна функция , которая монотонной не является. Тогда обязательно внутри [а,в] найдется точка Как видим, такие точки графика явл. вершинами горбов или впадин. Характерно, что с одной стороны т.
Определение 1. Говорят что функция у=f(x) им. в точке Обозначают минимум -min, максимум- max. Саму т Если сущ. такая окрестность точки, что для х¹ Min и max объединяют одним понятием- экстремум. Само определение экстремума показывает их возможное существование лишь во внутренних точках обл. определения функции и не может сущ. экстремум в граничных точках. Точки экстремума нельзя смешивать с точками, где функция принимает свое наибольшее или наименьшее значение для всей области определения функции. Min и max явл. наиб. и наим. значениями функции лишь в достаточно малых окрестностях. Вполне возможно, что min в одной точке больше max в другой. Так f( Однако ,если непрерывная функция им несколько минимумов и максимумов на [а,в], то наибольшее и наименьшее значение функции на [а,в] находится среди них или на концах сегмента. Поэтому нужно уметь находить точки экстремумов. Делают это спомощью производных.
x Теорема (неоходимое условие экстремума). Если дифференцируемая (им. конечную производную) функция у=f(x) имеет экстремум в т. Доказательство. Т.к. в т.
Итак, теорема утверждает, что экстремум может быть у дифференцируемой функции лишь в тех точках, где производная обращается в ноль, но не обязательно в каждой. Но экстремумы функция может иметь и в точках, где производная не существует вовсе или равна бесконечности. Пример. 1) f(x)=|x|. Не имеет производной в т.
|
|||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 157. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 функцию называют возрастающей (убывающей), если для любых
функцию называют возрастающей (убывающей), если для любых  из условия
из условия  следует
следует 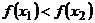
 . Если всегда
. Если всегда  , то
, то  называется постоянной на
называется постоянной на 

 и
и 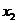 Î[а,в] при чем а£
Î[а,в] при чем а£  ] функция удовл. всем условиям т-мы Лагранжа, поэтому
] функция удовл. всем условиям т-мы Лагранжа, поэтому  С
С 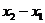 )³0 отсюда f(
)³0 отсюда f(  и
и  ³0, те f '(
³0, те f '(  =0. Касательная параллельна оси ох.
=0. Касательная параллельна оси ох.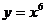 :
:  - область определения.
- область определения.  . Для x<0
. Для x<0  <0 – ф-я убывает, для x>0
<0 – ф-я убывает, для x>0 

 y
y
 Условие т-мы , действительно, лишь необходимое, оно не явл достаточным. Так для функции у=х3 в т.х0=0 , у'(0)=0, однако экстремума нет, функция монотонно возрастает.
Условие т-мы , действительно, лишь необходимое, оно не явл достаточным. Так для функции у=х3 в т.х0=0 , у'(0)=0, однако экстремума нет, функция монотонно возрастает. 2)у=f(x)=
2)у=f(x)=  =х
=х  , у'=
, у'=  , f '(0)=¥. Касательная к графику параллельна оси оу (сама ось oy).
, f '(0)=¥. Касательная к графику параллельна оси оу (сама ось oy).