Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Алгоритм ближайшего соседа.ПРАКТИЧЕСКИЕ ЗАНЯТИЯ 3, ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ГРАФЫ Графы возникли в восемнадцатом столетии, когда известный математик, Леонард Эйлер, пытался решить теперь уже классическую задачу о Кенигсбергских мостах. В то время в городе Кенигсбергебыло два oстровa, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 7.1. 3адача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра - с мостами, которыми связаны эти части. Как мы покажем в § 7.1, Эйлеру удалось доказать, что искомого маршрута обхода города не существует.
Рисунок 7.1. Схема старого Кенигсберга В этой главе мы вводим стандартную терминологию, используемую в теории графов, и разбираем несколько конкретных задач решаемых с помощью графов. В частности, мы познакомимся с классом графов, называемых деревьями. Деревья – естественная модель, представляющая данные, организованные в иерархичную систему. Поиск по дереву для выделения отдельных предметов и сортировка данных в дереве представляет собой важные точки приложения усилий в информатике. В приложении к этой главе мы займемся сортировкой и поиском данных, организованных в деревья. Графы и терминология На рис. 7.1 изображены семь мостов Кенигсберга так. как они были расположены в восемнадцатом столетии. В задаче, к которой oбpaтился Эйлер, спрашивается: можно ли найти маршрут прогулки, который проходит ровно один раз по каждому из мостов и начинается и заканчивается в одном и том же месте города?  Модель задачи - это граф, состоящий из множества вершин и множества ребер, соединяющих вершины. Вершины А, В, С и D символизируют берега реки и острова, а ребра а,в, c,d,f и g обозначают семь мостов (см. рис. 7.2). Искомый маршрут (если он существует) соответствует обходу ребер графа таким образом, что каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки по мосту.
Рисунок 7.2. Модель задачи о мостах Кенигсберга Граф, в котором найдется маршрут, найдется маршрут, начинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется зйлеровым графом. Последовательность вершин (может быть и с повторениями), через которые проходит искомый маршрут, как и сам маршрут, называется эйлеровым циклом. Эйлер заметил, что если в графе есть эйлеров цикл, то для каждого ребра, ведущего в какую-то вершину, должно найтись другое ребро, выходящее из этой вершины1, и получил из этого простого наблюдсния такой вывод: если в данном графе существует эйлеров цикл, то к каждой вершине должно подходить четное число ребер. Кроме того, Эйлеру удалось доказать и противоположное утверждение, так что граф, в котором любая пара вершин связана некоторой последовательностью ребер, является Эйлеровым тогда и только тогда, когда все его вершины имеют четную степень. Степенью вершины vназывается число δ(v)ребер, ей инцидентных2 . Теперь совершенно очевидно, что в графе, моделирующем задачу о мостах Кенигсберга, эйлерова цикла найти нельзя. Действительно, степени всех его вершин нечетны: δ(B) = δ(С) = δ(D) = 3 и δ(A) = 5. С легкой руки Эйлера графы, подобные тому, который мы исследовали при решении задачи о мостах, стали использовать при решении многих практических задач, а их изучение выросло в значительную область математики. Простой граф определяется как пара G = (V, Е), где V - конечное множество вершин, а Е - конечное множество ребер, причем не может содержать петель (ребер, начинающихся и заканчивающихся в одной вершине) и кратных ребер (кратными называются несколько ребер, соединяющих одну и ту же пару вершин). Граф, изображенный на рис. 7.2. не является простым, поскольку, например, вершины А и В соединяются двумя ребрами (как раз эти ребра и называются кратными). Две вершины u и v в простом графе называются смежными, если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершине u(и v). Таким образом, мы можем представлять себе множество Е ребер как множество пар смежных вершин, определяя тем самым нерефлексивное, симметричное отношение на множестве V. Отсутствие рефлексивности связано с тем, что в простом графе нет петель, т. е. ребер, оба конца которых находятся в одной вершине. Симметричность же отношения вытекает из того факта, что ребро е, соединяющее вершину и с v, соединяет и v с и (иначе говоря, ребра не ориентированы, т. е. не имеют направления). Единственное ребро простого графа, соединяющее пару вершин u и v, мы будем обозначать как иv (или vи). Логическая матрица отношения на множестве вершин графа, котopoe задается его ребрами, называется ,матрицей смежности. Симметричность отношения в терминах матрицы смежности М означает, что Мсимметрична относительно главной диагонали. А из-за нерефлексивности этого отношения на главной диагонали матрицы Мстоит символ «Л». Пример 7.1. Нарисуйте граф G(V, Е)с множеством вершин V = {а, Ь, с, d, е} и множеством ребер E= {ab, ae, bc, bd, ce, de}. Выпишите его матрицу смежности. Решение. Граф G показан на рис. 7.3.
Рисунок 7.3. Его матрица смежности имеет вид:
Для восстановления графа нам достаточно только тех элементов матрицы смежности, которые стоят над главной диагональю. Подграфом графа G = (V, E) называется граф G’ = (V’, E’), в котором E’ C E и V’ C V. Пример 7.2Найдите среди графиков H, K и L, изображенных на рис. 7.4, подграфы графа G. Решение.Обозначим вершины графов G, H и K как показано на рис. 7.5. Графы H и K – подграфы в G, как видно из наших обозначений. Граф L не является подграфом в G, поскольку у него есть вершина индекса 4, а у графа G такой нет. Маршрутом длины k в графе G называется такая последовательность вершин v0 , v1 , …, vk ,что для каждого i = 1, …, k пара vi – 1 vi образует ребро графа. Мы будем обозначать такой маршрут через v0 v1 … vk .Например 1 4 3 2 5 – это маршрут длины 4 в графе G из примера 7.2.
K L
Рисунок 7.4. Циклом в графе принято называть последовательность вершин v0 , v1 , … , vk ,каждая пара которых является концами одного ребра, причем v0 = v1 , а остальные вершины ( и ребра) не повторяются. Иными словами, цикл – это замкнутый маршрут, проходящий через каждую свою вершину и ребро только один раз G H K
1 2
4 5 4 3 4 5 Рисунок 7.5
Пример 7.3.Найдите циклы в графе G из примера 7.2.
Решение.В этом графе есть два разных цикла длины 5: 1 3 2 5 4 1 и 1 2 5 4 3 1 Мы можем пройти эти циклы как в одном направлении так и в другом, начиная с произвольной вершины цикла. Кроме того, в графе есть три разных цикла длины 4:
1 2 5 4 1, 1 2 3 4 1 и 2 5 4 3 2,
и два цикла длины 3:
1 2 3 1 и 1 3 4 1.
Граф, в котором нет циклов, называется ацикличным. Структуры деревьев, которые возникают в вычислениях , представляют собой частный случай ацикличных графов. Позже в этой главе мы ими займемся. Граф, называют связным, если любую пару его вершин соединяет какой – нибудь маршрут. Любой общий граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа и обозначается через c(G). Вопросы связности имеют важное значение в приложениях теории графов к компьютерным сетям. Следующий алгоритм применяется для определения числа связности графа.
Алгоритм связности.
Пусть G = (V, E) – граф. Алгоритм предназначен для вычисления значения c = c(G), т.е. числа компонент связности данного графа G.
begin V’ :=V; c:=0; whileV’≠ ø do begin Выбрать y Є V’ Найти вершины, соединяющие маршрутом с у; Удалить вершину у из V’ и соответствующие ребра из Е; c:=c+1; end end Пример 7.4.Проследите за работой алгоритма связности на графе, изображенном на рис. 7.6.
1 5
2 6
3 7
8 4
Рисунок 7.6.
Решение.Смотри табл. 7.1.
Таблица 7.1.
Итак, c(G) = 3. Соответствующие компоненты связности приведены на рис. 7.7.
1
6 2
3
8 4
Рисунок 7.7.
Гамильтоновы графы Мы начали эту главу с изучения эйлеровых графов, обладающих замкнутым маршрутом, который проходит по всем ребрам графа ровно один раз. Похожая задача состоит в поиске цикла, проходящего через каждую вершину графа в точности один раз. Такой цикл, если он существует, называется гамильтоновым, а соответствующий граф – гамильтоновым графом. Гамильтоновы графы служат моделью при составлении расписания движения поездов, для телекоммуникационных сетей и т.д. В отличие от задачи Эйлера, простого критерия гомильтоновости графа пока не известно. Поиск хорошего критерия остается одной из главных нерешенных задач теории графов. Полный граф К5 изображен на рис. 7.8. Его цикл a b c d e a, очевидно, является гамильтоновым. В нем есть и другие гамильтоновы циклы. Поскольку каждая вершина смежна с остальными, то начиная с вершины а, в качестве второй вершины цикла мы можем выбрать любую из четырех оставшихся. Далее у нас будет три варианта для выбора третьей вершины и два для четвертой, после чего мы вернемся в вершину а. Таким образом, у нас есть 4 · 3 · 2 = 24 цикла. Поскольку каждый цикл можно проходить как в одном направлении, так и в другом, то реально в графе К5 есть только 12 разных гамильтоновых циклов1.
a c
e d
Рисунок 7.8. Полный граф К5
Поиск гамильтонова цикла (если он существует) в произвольном (связном) графе – задача далеко не всегда простая. Ответ на вопрос о гамильтоновости графа может оказаться довольно трудоемким.
Пример 7.5.Покажите что граф, изображенный на рис. 7.9, не является гамильтоновым.
b
a c
Рисунок 7.9. Пример не гамильтонова графа Решение.Предположим, что в связном графе найдется гамильтонов цикл. Каждая вершина v включается в гамильтонов цикл С выбором двух инцидентных с ней ребер, а значит, степень каждой вершины в гамильтоновом цикле (после удаления лишних ребер) равна 2. Степени вершин данного графа - 2 или 3. вершины степени 2 входят в цикл вместе с обоими инцидентными с ними ребрами. Следовательно, ребра ab, ae, cd, cb, hi, hg и ij в том или ином порядке входят в гамильтонов цикл С (см. рис. 7.10.). Ребро bf не может быть часть цикла С, поскольку каждая вершина такого цикла должна иметь степень 2. Значит, ребра fi и fg обязаны входить в цикл С, чтобы включить в него вершину f. Но тогда ребра je и gd никак не могут принадлежать циклу С, поскольку в противном случае в нем появятся вершины степени три. Это вынуждает нас включить в цикл ребро ed, что приводит нас к противоречию: ребра, которые мы были вынуждены выбрать, образуют два несвязных цикла, а не один, существование которого мы предполагали. Вывод: граф, изображенный на рисунке 7.10, не является гамильтоновым. Гамильтоновы графы применяются для моделирования многих практических задач. Основой всех таких задач служит классическая задача коммивояжера. Коммивояжер должен совершить поездку по городам и вернуться обратно, побыв в каждом городе ровно один раз, сведя при этом затраты на передвижение к минимуму.
f
a c h i
j g
e d
Рисунок 7.10. Ребра входящие в гамильтонов цикл С Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге2. Для решения задачи нам необходимо найти гамильтонов цикл минимального общего веса. К сожалению, эффективный алгоритм решения данной задачи пока не известен. Для сложных сетей число гамильтоновых циклов, которые необходимо просмотреть для выделения минимального, непомерно огромно. Однако существуют алгоритмы поиска субоптимального решения. Субоптимальное решение необязательно даст цикл минимального общего веса, но найденный цикл будет, как правило, значительно меньшего веса, чем большинство произвольных гамильтоновых циклов! Один из таких алгоритмов мы сейчас и изучим.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Тема: АЛГОРИТМЫ ПОИСКА СУБОПТИМАЛЬНОГО РЕШЕНИЯ. Алгоритм ближайшего соседа. Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин V. Цикл, полученный в результате работы алгоритма, будет совпадать с конечным значением переменной маршрут, а его общая длина – конечное значение переменной w.
Begin Выбрать v Є V; маршрут:= v; w:=0; v':=v; Отметить v': whileостаются неотмеченными вершины do begin Выбрать неотмеченную вершину u, ближайшую к v’; маршрут:=маршрут u; w:=w+вес ребра v’u; v’:=u; Отметить v’; end маршрут:= маршрут v; w:=w+вес ребра v’u; End Пример 7.6.Примените алгоритм ближайшего соседа к графу, изображенному на рисунке 7.11. За исходную вершину возьмите вершину D.
6 10
C D 3
Рисунок 7.11. Решение.Смотрите табл.7.2
Таблица 7.2
В результате работы алгоритма был найден гамильтонов цикл DCABD общего веса 24. Делая полный перебор всех циклов в этом маленьком графе, можно обнаружить еще два других гамильтоновых цикла: ABCDA общего веса 23 и ACBDA общего веса 31. В полном графе с двадцатью вершинами существует приблизительно 6,1 · 1016 гамильтоновых циклов, перечисление которых требует чрезвычайно много машинной памяти и времени.
Деревья Как уже упоминалось, есть класс графов, называемых деревьями, которые особенно интенсивно используются в вычислительных приложениях. Граф G = (V, E) называется деревом, если он связен и ацикличен(т.е. не содержит циклов). Пусть G = (V, E) – граф с n вершинами и m ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которых G является деревом:
· Любая пара вершин в G соединена единственным путем. · G связен и m = n – 1. · G связен, а удаление хотя бы одного его ребра нарушает связность графа. · G ацикличен, но если добавить хотя бы одно ребро, то в G появится цикл.
Эквивалентность большинства из этих условий устанавливается без особого труда. Наиболее сложно разобраться со вторым из них. В следующем примере мы докажем, что дерево с n вершинами имеет ровно n – 1 ребро. Пример 7.7.Докажите с помощью индукции по числу вершин, что для дерева T с n вершинами и m ребрами выполнено соотношение: m = n – 1. Решение.Поскольку дерево с единственной вершиной вообще не содержит ребер, то доказываемое утверждение справедливо при n = 1. Рассмотрим дерево Т с n вершинами (и m ребрами), где n > 1 и предположим, что любое дерево с k < n вершинами имеет ровно k – 1 ребро. Удалим ребро из Т. По третьему свойству дерево Т после этой процедуры превратится в несвязный граф. Получится ровно две компоненты связности, ни одна из которых не имеет циклов (в противном случае исходный граф Т тоже содержал бы циклы и не мог бы быть деревом). Таким образом, полученные компоненты связности – тоже деревья. Обозначим новые деревья Т1 и Т2. Пусть n1 – количество вершин у дерева Т1 , а n2 – y T2. Поскольку n1 + n2 = n, то n1 < n и n2 < n. По предположению индукции дерево Т1 имеет n1 – 1 ребро, а Т2 – n2 – 1. Следовательно, исходное дерево Т насчитывало ( с учетом одного удаленного) (n1 – 1) + (n2 – 1) + 1 = n – 1 ребро, что и требовалось доказать. Несложно доказать, что в любом связном графе найдется подграф, являющийся деревом. Подграф в G , являющийся деревом и включающий в себя все вершины G, называется остовным деревом. Остовное дерево в графе G строится просто: выбираем произвольное его ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. Благодаря примеру 7.7, мы знаем, что для построения остовного дерева в графе из n вершин необходимо выбрать ровно n – 1 ребро.
Пример 7.8.Найдите два разных остовных дерева в граве, изображенном на рис. 7.12.
Рисунок 7.12. Связный граф G Решение.В этом графе существует несколько остовных деревьев. Одно из них получается последовательным выбором ребер: a, b, d, и f. Другое – b, c, e и g. Названные деревья показаны на рисунке 7.13. Процесс, описанный в примере 7.8, можно приспособить для решения задачи кратчайшего соединения: Нужно построить железную сеть, связывающую некоторое число городов. Известна стоимость строительства отрезка путей между любой парой городов. Требуется найти сеть минимальной стоимости. На языке теории графов нам нужно в нагруженном графе найти остовное дерево наименьшего общего веса. Такое дерево принято называть минимальным остовным деревом или, сокращенно МОД. В отличие от задачи коммивояжера, здесь есть эффективный алгоритм, находящий действительно минимальное остовное дерево. Он похож на алгоритм Прима.
Рисунок 7.13. Остовные деревья графа G
Алгоритм поиска минимального остовного дерева.Пусть G = (V, E) – связной взвешенный граф. Алгоритм строит МОД в графе G, последовательно выбирая ребра наименьшего возможного веса до образования остовного дерева. МОД в памяти компьютера хранится в виде множества Т ребер.
Begin e:=ребро графа G с наименьшим весом; T:={e}; E':=E\{e} whileE' ≠ ø begin e':= ребро из E' наименьшего веса; Т:= Т U {e'}; E' := множество ребер из E' \{T}, чьё добавление к Т не ведет к образованию циклов; end End Пример 7.9.В таблице 7.3 дано расстояние (в милях) между пятью деревнями A, B, C, D и E. Найдите минимальное остовное дерево.
Таблица 7.3
Решение.Ребра выбираются следующим образом: первое – 1 DE веса 2; второе – AC веса 3; третье – СЕ веса 7. на этой ступени строящееся дерево выглядит так, как на рис. 7.14
Рисунок 7.14. Вид дерева после трех шагов
Следующие повесу ребра – AD, AE и CD, каждое из которых имеет вес 9. Однако какое бы из них мы не добавили, получится цикл. Поэтому перечисленные ребра следует исключить из доступных для строительства. Далее идут ребра ВС и ВD веса 11. Можно присоединить любое из них, получив при этом два разных МОД: {AC, BC, CE, DE} или {AC, BD, CE, DE} веса 23 каждое. Зачастую, нам хотелось бы иметь деревья, представляющие собой формацию с учетом естественной иерархической структуры, такие как, например, генеалогическое дерево (рис.7.15). На нем показаны некоторые члены семьи Бернулли, каждый из которых был известным швейцарским математиком. Генеалогическое дерево можно изобразить и более сжато. Схема приведенная на рисунке 7.16, представляет собой пример так называемого дерева с корнем. Деревом с корнем называется дерево с одной выделенной вершиной. Именно эта выделенная вершина и является корнем дерева. Вершины дерева, лежащие непосредственно под корнем, называются сыновьями. С другой стороны, вершина, стоящая непосредственно перед сыном, называется ее отцом.
Рисунок 7.15. Династия Бернулли
Рисунок 7.16. Схема генеалогического древа Бернулли
Древо с корнем можно определить рекуррентным образом. Отдельная вершина является деревом с корнем (она же служит и корнем такого дерева). Если Т1, Т2, …, Тk - несвязные друг с другом деревья с корнями v1, v2, …, vk, то граф, получающийся присоединением новой вершины v к каждой из вершин v1, v2, …, vk отдельным ребром, является деревом Т с корнем v. Вершины v1, …, vk графа Т – это сыновья корня v. Мы изображаем такое дерево с корнем, расположенным наверху, и сыновьями, стоящими ниже, непосредственно под корнем (см. рис. 1.17). Каждую вершину дерева с корнем можно рассматривать как корень другого дерева, которое «растет» из него. Мы будем называть его поддеревом дерева Т. Как мы уже говорили, вершина на самом верху дерева – его корень, а вот те, которые находятся в самом низу дерева (не имеют сыновей) принято называть листьями. Остальные вершины, отличные от корня и листьев, называют внутренними. Область применения деревьев с корнями обширна. Это, например, и информатика, и биология, и менеджмент. Для приложения к информатике наиболее важны так называемые двоичные или бинарные деревья с корнем. Двоичное дерево отличает от остальных то, что каждая его вершина имеет не более двух сыновей. В двоичном дереве с корнем вниз от каждой вершины идет не более двух ребер.
v1 v2 vk
T1 T2 Tk
Рисунок 7.17.
Таким образом, можно сказать, что каждой вершине двоичного дерева с корнем соответствует не более, чем два поддерева, которые принято называть левыми и правыми поддеревьями этой вершины. Если оказалось, что у какой то вершины дерева отсутствует потомок слева, то ее левое поддерево называют нулевым деревом (т.е. нулевое дерево – это дерево без единой вершины). Аналогично, если у вершины отсутствует правый потомок, то ее правое поддерево будет нулевым.
Пример 1.10.Пусть Т – двоичное дерево с корнем, изображенное на рисунке 7.18.
Рисунок 7.18. Двоичное дерево с корнем Т
Определите (а) корень Т; (б) корень левого поддерева вершины В; (в) листья Т; (г) сыновей вершины С.
Нарисуйте двоичное дерево с корнем Т', полученное из Т перестановкой левых и правых поддеревьев к каждой вершины.
Решение.(а) А; (б) D; (в) G, H, E, I и J; (г) F. Двоичное дерево с корнем Т' начерчено на рис. 7.19.
Рисунок 7.19. Двоичное дерево с корнем Т'
Набор упражнений 7.1.Объясните, почему сумма степеней всех вершин простого графа G совпадает с удвоенным числом его ребер. Этот факт называют леммой об эстафете. Используя эту лемму, покажите, что в любом полном графе Kn c n вершинами есть ровно n(n – 1)/2 ребер. Для каких значений n граф Kn будет эйлеровым?
7.2.Опираясь на принцип Дирихле, докажите, что если простой граф G имеет более одной вершины, то у него найдутся по крайней мере две вершины одинаковой степени.
7.3.Нарисуйте граф, чья матрица смежности имеет вид:
Опишите матрицу смежности полного графа Kn .
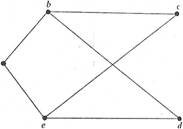
7.4. Введя подходящие обозначения вершин, для каждого из графов на рисунке 7.20 подберите соответствующую матрицу смежности из перечисленных ниже.
Рисунок 7.20.
(а) (б) (с) 7.5. Какие из графов на рис.7.12 могут являться подграфами графа из упражнения 7.3
Рисунок 7.21. Кандидаты в подграфы
7.6. Найдите гамильтоновы циклы в графе на рис.7.22.
Рисунок 7.22.
Найдите в нем циклы длины 3, 4, 5, 6 и 7.
7.7.На рисунке 7.23 изображен граф Петерсена Р. b
a c
Рисунок 7.23. Граф Петерсена
Найдите в нем цикл длины 9. Покажите, что Р не является гамильтоновым.
7.8. Используйте алгоритм ближайшего соседа для поиска гамильтонова цикла в нагруженном графе (рис.7.24), взяв за исходную (а) вершину А; (б) вершину D.
A
B C
Рисунок 7.24. Нагруженный граф 7.9. Выясните, являются ли графы, задаваемые следующими матрицами смежности, деревьями:
7.10.Известно, что дерево Т имеет три вершины степени 3 и четыре вершины степени 2. Остальные вершины дерева имеют степень 1. Сколько вершин степени 1 есть у дерева Т? (Указание: обозначьте число вершин дерева Т через n и примените лемму об эстафете.)
7.11.Лесом называют граф (не обязательно связный), каждая компонента связности которого – дерево. Пусть G – лес с n вершинами и k компонентами связности. (а) Докажите, что G имеет n – k ребер. (б) Покажите, что если в каждой компоненте связности леса G есть более одной вершины, то G содержит по крайней мере 2k вершин степени 1. (в) Нарисуйте лес с девятью вершинами и шестью ребрами, в котором не больше пяти вершин степени 1.
7.12.Найдите минимальное остовное дерево графа, изображенного на рис.7.25.
A
C F
H
Рисунок 7.25.
7.13. В таблице 7.4 приведены расстояния (в милях) между шестью городами Ирландии.
Таблица 7.4
Используя алгоритм поиска минимального остовного дерева, найдите сеть дорог минимальной общей длины, связывающую все шесть городов.
7.13.Глубина вершины v дерева с корнем Т определяется как длина единственного пути от нее к корню дерева. Глубина графа Т – это максимальная глубина его вершин. (а) Начертите следующие деревья: (i) дерево с корнем глубины 1 с шестью вершинами; (ii) полное двоичное дерево с корнем глубины 2; (iii) дерево с корнем глубины 3, каждая вершина глубины i (i ≥ 0) которого имеет (i + 1) сына. (б) Покажите индукцией по n, что полное двоичное дерево с корнем глубины n имеет 2n листьев.
(Полным, называется двоичное дерево с корнем, у которого все вершины (за исключениям листьев) имеют по два сына.)
Краткое содержание главы
Граф G = (V, E) состоит из множества V, чьи элементы называют вершинами графа, и множества Е его ребер, соединяющих некоторые пары вершин.
Вершины u и v графа называют смежными, если они соединены каким – то ребром e, про которое говорят, что оно инцидентно вершинам u и v.
Степенью вершины v считают число δ(v) ребер графа, инцидентных v.
Граф, в котором существует маршрут (называемый эйлеровым), начинающийся и заканчивающийся в одной и той же вершине и проходящий по каждому ребру графа ровно один раз, называется Эйлеровымграфом. Связный граф с двумя или более вершинами является эйлеровым тогда и только тогда, когда каждая его вершина имеет четную степень.
Лемма об эстафетеутверждает, что сумма степеней вершин произвольного графа G = (V, E) равна удвоенному числу его ребер.
Простымпринято называть граф G = (V, E) с конечным множеством вершин V и конечным множеством ребер E , в котором нет петель и кратных ребер.
Логическая матрица отношения на множестве вершин простого графа G, которое задается его ребрами, называется матрицей смежности.
Подграфомграфа G = (V, E) называют граф G' = (V', E') в котором E' C E и V' C V.
Маршрутомдлины k в графе называют такую последовательность различных вершин v0,v1, …,vk, в которой каждая пара соседних вершин vi – 1 vi соединена ребром.
Цикломв графе является замкнутый маршрут v0,v1, …, v0, у которого все вершины, кроме первой и последней различны.
Граф, не содержащий циклов, называют ацикличным.
Связным является тот граф, в котором каждая пара вершин соединена маршрутом.
Количество компонент связности графа можно подсчитать с помощью алгоритма связности.
Гамильтоновым называют такой цикл в графе, который проходит через каждую вершину графа, причем только один раз. Граф в котором существует гамильтонов цикл, называют гамильтоновым. Задача коммивояжерасостоит в поиске гамильтонова цикла минимального общего веса в нагруженном графе. Алгоритм ближайшего соседапозволяет найти субоптимальное решение задачи коммивояжера.
Связный ацикличный граф G = (V, E) является деревом. Следующие утверждения о связном графе G = (V, E) c n вершинами и m ребрами эквивалентны:
(а) G – дерево; (б) любую пару вершин G связывает единственный путь; (в) G связен и m = n – 1; (г) G связен, а удаление любого его ребра нарушает его свойство; (д) G ацикличен, но соединяя любую пару вершин новым ребром, мы получаем цикл.
Остовным деревом графа G называют такой его подграф, который является деревом и содержит все вершины графа G. Алгоритм поиска минимального остовного деревапозволяет найти остовное дерево минимального общего веса в нагруженном графе и может быть использован для решения задачи поиска кратчайшего соединения.
Дерево с одной выделенной вершиной называют деревом с корнем, а выделенную вершину - его корнем. Вершины, стоящие непосредственно под вершиной v (и соединенные с ней ребрами), называют сыновьями вершины v. Вершины расположенные в самом низу дерева (они не имеют сыновей), называются листьями. Вершины, отличные от корня и листьев, называют внутренними вершинами графа. Нулевое дерево– это дерево, не имеющее ни одной вершины.
Каждая вершина дерева с корнем Т является корнем какого – другого дерева, называемого поддеревом Т. В двоичном дереве с корнемкаждая вершина имеет не более двух сыновей, а два поддерева вершины v называют левым и правым поддеревьями, ассоциированными с v. Двоичное дерево с корнем называют полным, если каждая его вершина, за исключением листьев, имеет ровно по два сына.
Глубинойвершины v дерева с корнем Т принято считать длину единственного маршрута, соединяющего его с корнем. Глубиной графа Т называют максимальную глубину его вершин.
Приложение. Сортировка и поиск
Двоичные деревья с корнем очень полезны при решении задач о выборе, в частности, о выборе такого сорта, при котором нужно классифицировать упорядоченные данные или вести в них поиск. Упорядоченные данные, такие как множество чисел, упорядоченных по величине или множество строк литер, упорядоченных лексикографически (в алфавитном порядке), можно организовать в виде вершин двоичного дерева с корнем в соответствии с их порядком. При этом мы стремимся к тому, чтобы данные, стоящие в левом поддереве данной вершины v были бы меньше данных, соответствующих этой вершине, а данные, расположенные в правом ее поддереве – больше. Дерево данных, удовлетворяющих указанному условию, называют двоичным деревом поиска. Например, в дереве двоичного поиска, приведенном на рисунке 7.26. слова фразы «У МОЕГО КОМПЬЮТЕРА ЕСТЬ ЧИП НА МАТЕРИНСКОЙ ПЛАТЕ» организованны именно таким образом. Заметим что каждое слово в левом поддереве любой вершины предшествует (относительно алфавитного порядка) слову, стоящему в этой вершине, а каждое слово ее правого поддерева следует за словом выбранной вершины.
Рисунок 7.26. Дерево двоичного поиска
Преимущественно организации упорядоченных данных в виде двоичного дерева поиска заключается в возможности создания эффективного алгоритма поиска каких то конкретных данных, включение новых данных в дерево и печати всей информации, содержащейся в дереве в виде упорядоченного списка. Предположим, что в университете хранится список студентов (упорядоченный в алфавитном порядке), в котором кроме фамилий и имен имеются дополнительные важные сведения о студентах. Допустим так же, что возникла необходимость найти какую – то информацию в списке или добавить новые записи к списку. Мы сейчас познакомимся с алгоритмами, которые осуществляют поиск конкретной информации, добавляют новых студентов к списку и выводят на печать все записи в алфавитном порядке. Записи о студентах организованы в двоичное дерево поиска (каждая запись соответствует одной вершине), и наши алгоритмы будут исследовать вершины этого дерева. Поскольку каждая вершина является так же и корнем некоторого двоичного дерева поиска, алгоритмы будут последовательно проверять левые и правые поддеревья вершин. Чтобы это осуществлять, необходимо приписать каждой вершине некоторый ключ для идентификации и ссылок на ее левое и правое поддеревья (в структурах данных для этих целей используются так называемые дважды связанные списки). Из всех ключей организуется линейно упорядоченное множество (в нашей ситуации оно упорядочено лексикографически). Алгоритм поиска определяет, является ли данная запись (ключ поиска) вершиной в двоичном дереве поиска, сравнивая ключ поиска с ключом корня дерева, и, при необходимости, осуществляет аналогичные сравнения в левом или правом поддеревьях. Поиск (дерево) begin if дерево нулевое then поиск:=ложь; else if ключ поиска = ключ корня then поиск:=истина; else if ключ поиска < ключ корня then поиск:=поиск(левое поддерево); else поиск:=поиск(правое поддерево); end Задача 1. Поскольку R>K, то поиск продолжается в правом поддереве вершины K. Так как R<T, процесс поиска переключается на левое поддерево вершины Т. Наконец, ввиду неравенства R≠M и отсутствия поддеревьев у вершины M, алгоритм заканчивается и сообщает, что искомая вершина не была найдена.
Рисунок 7.27.
Алгоритм вставки вставляет новые вершины (ключи вставок) в двоичное дерево поиска, создавая при этом новую вершину слева или справа от уже существующей. Это делается таким образом, чтобы все ключи вершин в получившемся дереве подчинялись установившемуся порядку. Вставка (запись, дерево) begin if дерево нулевое then добавить новую вершину; else if ключ вставки = ключ корня then вывести на печать: «запись содержится в дереве»; else if ключ вставки < ключ корня then вставка:=вставка (запись, левое поддерево); else вставка:=вставка (запись, правое поддерево); end Задача 2.Проследите за работой алгоритма вставки на примере вершин R, A и L в дерево из задачи 1. Решение.Поскольку R>K, мы применяем алгоритм вставки к правому поддереву вершины K. Далее мы видим, что R<T. Значит, алгоритм вставки переключится на левое поддерево вершины Т. Так как R>M и правое поддерево вершины M нулевое, то мы ставим вершину R справа от М и получаем дерево, изображенное на рисунке 7.28. Теперь вставим A и L, построив дерево, показанное на рисунке 7.29.
Рисунок 7.28.
Алгоритм вставки можно использовать для создания двоичного дерева поиска, начиная с нулевого дерева и последовательно добавляя новые данные в удобном для нас порядке. Например, дерево поиска на рис.7.26 является результатом применения алгоритма вставки к нулевому дереву в процессе добавления слов фразы «У МОЕГ КОМПЬЮТЕРА ЕСТЬ ЧИП НА МАТЕРИНСКОЙ ПЛАТЕ» в том порядке, в котором они в ней записаны.
Рисунок 7.29.
Алгоритм правильного обхода выводит на печать всю информацию, содержащуюся в двоичном дереве поиска, в надлежащем порядке. При этом все вершины дерева осматриваются в определенном порядке. Алгоритм работает следующим образом. Для каждой вершины, начиная с корня, печатается вся информация, содержащаяся в вершинах левого поддерева. Затем выводится информация, хранящаяся в этой вершине, и наконец, информация, соответствующая вершинам правого поддерева. Правильный обход (дерево) begin ifдерево нулевое then ничего не делать; else begin правильный обход (левое поддерево); напечатать корневой ключ; правильный обход (правое поддерево); end end Задача 3.Примените алгоритм правильного обхода к дереву, полученному в задаче 2 после вставки R, A и L. Решение. После работы алгоритма над указанным деревом получается список:
A, C, K, L, M, R, T, V. Он соответствует обходу дерева против часовой стрелки (рис.7.30) и печати информации, содержащейся в вершинах, как только вы прошли под вершиной.
Рисунок 7.30 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 1668. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 G H
G H 1 2 1 2 3
1 2 1 2 3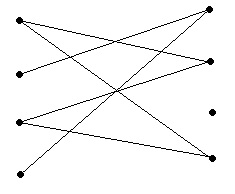
 5
5 b
b
 b
b A B
A B