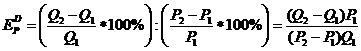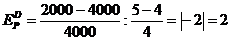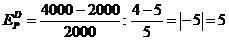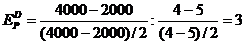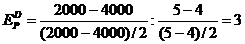Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Примеры задач оптимизации в экономике и финансахПрактика – занятие 1. ЗаданиеНайти ОР и ОДР и определить координаты угловых точек ОДР 1.
4.
7.
10.
Практика 2. Решение задач на экстремум графическим способом Задача. Решить графическим методом типовую задачу оптимизации. При производстве двух видов продукции используется 4 типа ресурсов. Норма расхода ресурсов на производство единицы продукции, общий объем каждого ресурса заданы в таблице.
Прибыль от реализации одной единицы продукции первого вида составляет 2 ден.ед., второго вида - 3 ден.ед. Задача состоит в формировании производственной программы выпуска продукции, обеспечивающей максимальную прибыль от ее реализации. Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на минимум, и почему?
Решение. 1. Экономико-математическая модель. Обозначим через Целевая функция - это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать
Ограничения по ресурсам:
2. Построение ОДР. Первое ограничение имеет вид  Второе ограничение имеет вид Третье ограничение Четвертое ограничение имеет вид В результате пересечения построенных четырех полуплоскостей получаем многоугольник, который и является областью допустимых решений задачи. Любая точка этого многоугольника удовлетворяет всем четырем функциональным неравенствам, а для любой точки вне этого многоугольника хотя бы одно неравенство будет нарушено. 3. Построение век тора-градиента и линии уровня. Для определения направления движения к оптимуму построим вектор-градиент V, координатами которого являются частные производные целевой функции. Чтобы построить такой вектор, нужно соединить точку (2;3) с началом координат. Затем построим линию уровня, перпендикулярно вектору-градиенту. 4. Поиск экстремума. Мысленно перемещаем линию уровня в направлении вектора-градиента до тех пор, пока она не выйдет из ОДР. Точка, в которой линия уровня покидает ОДР, будет точкой optimum. Находим координаты этой точки. Записываем систему уравнений для линий, пересекающихся в opt точке. В результате решения системы находим: Координаты opt точки подставляем в уравнение целевой функции и находим max (f) = 2*4+3*2 = 14 ден.ед.
5.Вывод. Предприятие получит максимальную прибыль 14 ден.ед. если будет выпускать 4 единицы товаров первого вида и 2 единицы товаров второго вида. Все другие сочетания объемов выпуска продукции дадут наименьшую прибыль.
Примеры. Исследовать на максимум и минимум функции, при условии, что на переменные наложены ограничения.
Практика 3. Решение задач, используя аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования. Задача. Для изготовления трех видов продукции используют два вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
Требуется: сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, сформулировать двойственную задачу и найти ее оптимальный план
Решение. 1. Экономико-математическую модель задачи. Обозначим через Целевая функция - это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать.
Ограничения по ресурсам:
2. Сформулируем экономико-математическую модель двойственной задачи. Переменные. Исходная задача содержит два ограничения по сырью I, II. Следовательно, в двойственной задаче две переменные: y1 - двойственная оценка сырья I или «цена» сырья I; y2 - двойственная оценка сырья II или «цена» сырья II. Целевая функция двойственной задачи формулируется на минимум. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи.
Необходимо найти такие «цены» yi на сырье, чтобы общая стоимость используемого сырья была минимальной. Ограничения. В исходной задаче три переменные, следовательно, в двойственной задаче три ограничения. В правых частях ограничений двойственной задачи стоят коэффициенты при неизвестных в целевой функции исходной задачи. Левая часть ограничений определяет стоимость сырья, затраченного на производство единицы продукции. Каждое ограничение соответствует определенному виду изделия.
Решая графическим методом двойственную задачу, ролучим: теневые цены сырья I, II соответственно равны Примеры. сформулировать двойственную задачу и найти ее оптимальный план
Практика №4 Тема: «Составление мат.модели и решение линейной оптимизационной задачи»
Задача 1. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 70 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна 30 и 20 усл.ед. соответственно. Определить оптимальный суточный объем производства первой и второй моделей радиоприемников.
Задача №2. Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 1000усл.ед. в месяц. Каждая минута радиорекламы обходится в 5 усл.ед., а каждая минута телерекламы – в 100 усл.ед. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что объем сбыта продукции, который обеспечивает каждая минута телерекламы, в 25 раз больше объема сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Задача №3. Фирма производит два вида продукции А и В. Объем сбыта продукции В составляет не более 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас второго ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 3 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны 20 и 40 усл.ед. соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Задача №4. Фирма производит два вида хлебобулочной продукции: булки и батоны. Для изготовления продукции используются два исходных продукта: мука и наполнители, расходы которых на 1кг продукции приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на булки превышает спрос на батоны, не более, чем на 100кг. Кроме того, установлено, что спрос на батоны не превышает 350кг. в сутки. Розничная цена 1кг булки 16 руб., батона – 14 руб. Какое количество хлебобулочной продукции каждого вида должна производить фирма, чтобы доход от реализации был максимальным?
Ответы: №1 ((60,25), L=2300), №2 ((18,18; 9,09), L=16,36) №3 ((11.1; 16,7), L=888,9) №4 (( ((11; 17) . огранич. не вып.) ((12, 16) L=880 ) Практика 5 Примеры задач оптимизации в экономике и финансах Теория. 1. Функция полезности с полным взаимозамещением благ: где коэффициент 2. Функция полезности с полным взаимодополнением благ: где
3.Задача потребительского выбора. Задача потребительского выбора имеет вид: Решение задачи потребительского выбора: либо графический метод решения задач линейного программирования, либо метод Лагранжа. Решением задачи является набор 4.Эластичность спроса по цене. Коэффициент ценовой эластичности спроса: процентного изменения количества спрашиваемой продукции к процентному изменению цены, вызвавшему это изменение спроса Q1 и Q2 — первоначальный и текущий объем спроса; P1 и Р2 — первоначальная и текущая цена. Формула центральной точки: Пример 1. Пусть товаром первого вида является кофе, второго – чай, а потребление этих продуктов в количествах Представим, что потребление кофе уменьшилось на В результате имеем: Отсюда найдем Таким образом, функция позволяет определить размер замещения одних товаров другими для того, чтобы полезность оставалась на неизменном уровне. Пример 2. Приобретается набор из двух товаров: кофе в количестве В случае (1) и увеличение (уменьшение) потребления кофе влечет увеличения (уменьшения) сахара. В случае (2) увеличение потребления кофе может привести к нарушению неравенства в (2) и, следовательно, к нарушению уровня полезности, если не увеличиться потребление сахара. Функция (2) применяется для определения полезности набора взаимодополняющих друг друга товаров. Пример 3. Оптимальный набор потребителя составляет 6 ед. продукта х1 и 8 ед. продукта Решение. Следуя принципу решения, получаем систему уравнений:
Подставив, вместо х1 - 6 ед., вместо х2 - 8 ед., получим: p1=20руб., p2=15руб. Итак, решение задачи потребительского выбора сводится к решению задач на условный экстремум. Пример 4. Цена товара колеблется в интервале от 4 до 5 ден. ед. При Px=4 ден. ед. объем спроса составляет 4000 ед. продукции. При Px = 5 ден. ед. — 2000 ед. Используя первоначальную формулу рассчитаем значение коэффициента ценовой эластичности для данного ценового интервала: Однако если в качестве базовой взять другую комбинацию цены и количества продукции, то получим: И в первом, и во втором случае спрос эластичный, но результаты отражают разную степень эластичности, хотя анализ мы проводим на одном и том же ценовом интервале. Для преодоления этого затруднения экономисты используют в качестве базовых средние величины уровней цены и количеств, т. е. или Практика №6 Тема: «Мат.модель транспортной задачи, решение задачи»
Задача №1. (Cдефицитом) Задача №3. (Cдефицитом) Данные заданы таблицей Данные заданы таблицей
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

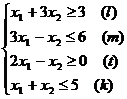 2.
2. 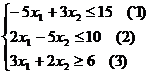 3.
3. 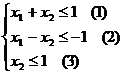
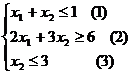 5.
5. 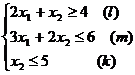 6.
6. 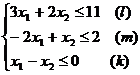
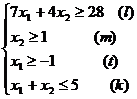 8.
8. 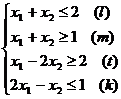 9.
9. 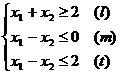
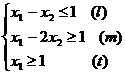 11.
11. 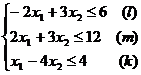 12.
12. 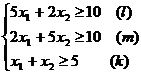
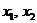 объемы производства соответствующего вида продукции (количество товаров каждого вида).
объемы производства соответствующего вида продукции (количество товаров каждого вида).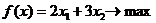
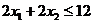
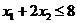
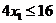
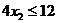
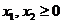
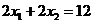 проходит через точки (0;6) и (6;0).
проходит через точки (0;6) и (6;0).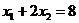 проходит через точки (0;4) и (8;0).
проходит через точки (0;4) и (8;0).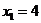 .
.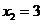 .
.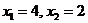
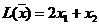
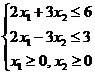 Ответ:
Ответ: 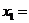 9/4
9/4 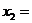 1/2 L=5
1/2 L=5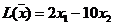
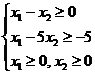 Ответ:
Ответ: 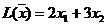
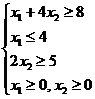 Ответ:
Ответ: 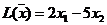
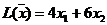
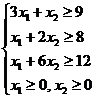 Ответ:
Ответ: 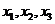 - число изделий каждого вида.
- число изделий каждого вида.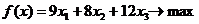
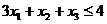
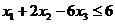
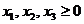
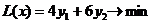
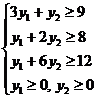
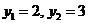 и L=26.
и L=26.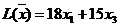
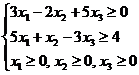
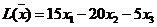
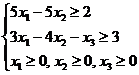
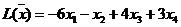
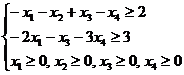
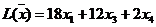
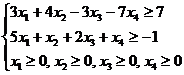
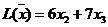
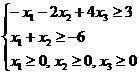
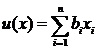
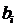 является числовой оценкой полезности от потребления единицы товара вида i.
является числовой оценкой полезности от потребления единицы товара вида i.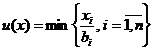
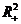 из уравнения
из уравнения 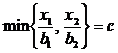 найдем
найдем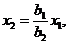 если
если 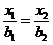 (1)
(1)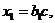 если
если 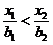 (2)
(2)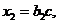 если
если 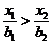 (3)
(3)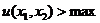 при ограничении
при ограничении 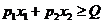 и условие
и условие 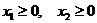 .
.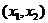 .
.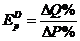 , где
, где 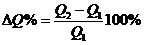
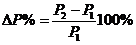 , тогда
, тогда 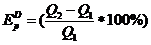 :
: 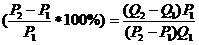
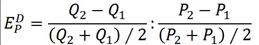
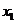 и
и 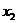 дает полезность, равную с , то есть
дает полезность, равную с , то есть 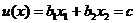 .
.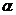 единиц. Тогда полезность упадет до уровня
единиц. Тогда полезность упадет до уровня 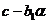 . Чтобы компенсировать эту потерю полезности надо увеличить потребление чая на величину
. Чтобы компенсировать эту потерю полезности надо увеличить потребление чая на величину 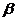 так, чтобы
так, чтобы 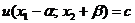
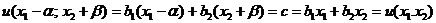
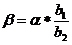 .
.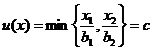
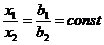
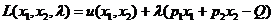 ,
, 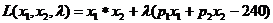
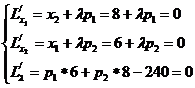
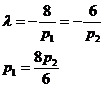
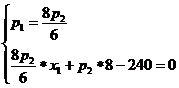
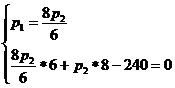 16p2=240 p2=15 p1=20
16p2=240 p2=15 p1=20