
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Семестр вопросы к экзамену (доказательства из конспекта лекций)ЛЕКЦИЯ 1 - 11.02.2014 *** Доказать, что градиент ортогонален к поверхности. *** Вывести формулу производной по направлению. *** Вывести формулу касательной плоскости к поверхности.
§ 2. Дифференцирование неявно и параметрически заданных функций *** Вывод формулы производной для параметрически заданной кривой. *** Вывод формулы производной Вывод формулы производных
§ 3. Дифференциал и формула Тейлора Определение дифференциала, отличие Вид формулы Тейлора. ЛЕКЦИЯ 2 - 18.02.2014 *** Вывод формул Тейлора для некоторых основных функций:
Понятие условного экстремума, пример
Глава 2. Неопределённые интегралы Введение. Определение первообразной и неопределённого интеграла. Свойство: F+C тоже является первообразной. § 1. Основные методы интегрирования.
1.1. Подведение под знак дифференциала примеры - 1.2. Замена переменной пример 1.3. Преобразования выражения под интегралом пример - пример - пример - Важное свойство в преобразованиях, всегда можно использовать
1.4. Интегрирование по частям. *** Доказать формулу «интегрирования по частям» Доказывается эта формула с помощью правила дифференцирования: Примеры: ЛЕКЦИЯ 3 - 25.02.2014 Примеры: Циклические интегралы. пример *** Вывод формулы  Пример. § 2.Интегрирование рациональных дробей. Про выделение целой части, сведение к правильной. Простейшие дроби (где знаменатель дальше не распадается на множители), их вычисление: Общий случай (когда знаменатель надо сначала разложить на множители, предварительно находить корни знаменателя). 1) Если все корни знаменателя разные, пример 2) Если есть кратные корни, + пример 3) Если есть комплексные корни, + пример ЛЕКЦИЯ 4 - 04.03.2014
§ 3.Интегрирование иррациональностей и тригонометрических функций.
Если корни разного порядка. *** Доказать, что замена замена
Интегрирование тригонометрических выражений.
Случай 1. Нечётная относительно cos функция в интеграле.
Замена:
Случай 2. Нечётная относительно sin функция в интеграле. Замена: Пример: Смысл всех этих подстановок: в результате их действия получается корень в чётной степени, так как тригонометрическая функция преобразуется к виду корня нечётной степени, и это делится или домножается ещё на корень из dx, в итоге в любом случае будет чётная степень корня. Случай 3. Суммарная степень нечётна, то есть Замена: Пример: Универсальная тригонометрическая подстановка при этом: Пример:
Интегрирование выражений типа
Пример Пример - Доказательство формулы
Доказать, что корень преобразуется в тригонометрическое выражение.
ЛЕКЦИЯ 5 - 11.03.2014 Глава 3. Определённый интеграл. § 1. Определение, свойства, методы вычислений
Определение. Свойства: 1. 2. 3. 4. 5. если 6. если 7. 8. если 9. существует такое 10. если f непрерывна то сущ. точка *** Теорема 1. *** Теорема 2. Ньютона-Лейбница. Пример Вид формулы интегрирования по частям для опред. интеграла. Особенности замены переменной в определённом интеграле (пересчёт пределов интегрирования, не возвращаться к старой переменной). Пример. § 2. Приложения определённых интегралов. Вычисление площадей. Пример с применением обратной функции для Вычисление объёмов тел вращения. *** Вывод формулы Пример: доказательство этим методом формулы объёма шара.
Длина дуги кривой. *** Вывод формулы в декартовых координатах для явно заданной кривой Для параметрически заданной в плоскости и пространстве:
Длина кривой в полярной системе координат:
ЛЕКЦИЯ 6 - 18.03.2014 § 3. Определённый интеграл и ряд Фурье.
Скалярное произведение функций (f,g). Норма функции. *** Вывод формулы коэффициента Фурье для произвольной ортогональной системы:
Основная ортогональная система. Ряд Фурье Свойства ряда Фурье при чётности или нечётности функции. Пример: разложить в ряд Фурье функцию ЛЕКЦИЯ 7 - 25.03.2014 § 4. Несобственные интегралы Несобственные интегралы. Вводные примеры: Определения несобственных интегралов 1-го (неограниченная D(f)) и 2-го рода (неограниченная E(f)). Сходимость, расходимость. *** Доказать, что несобственный интеграл 1-го рода Примеры: *** Теорема 1. *** Следствие. Теорема 2. Признак сравнения в конечной форме. Если Пример. Теорема 3. Признак сравнения в предельной форме. Если Пример. Определение абсолютной сходимости. Из абсолютной сх-сти следует обычная (доказывается по признаку сравнения). Понятие преобразования Лапласа:
ЛЕКЦИЯ 8 - 01.04.2014 Глава 4. Кратные интегралы, элементы теории поля. § 1. Кратные интегралы.
Определение. Геометрический и физический смысл. Кратные интегралы, двойные, тройные. Свойства. Вычисление двойных интегралов по прямоугольной и непрямоугольной области. Геометрический смысл. Объём под поверхностью. Сведение к повторным: интегрирование величин всех площадей криволинейных трапеций в сечениях по перпендикулярному направлению. Аналогично, массив в программировании может быть не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле: for i : = 1 to 10 do for j : = 1 to i do read (a[i,j]); end; end;
Примеры: Смена порядка интегрирования: Пример:
Вычисление тройных интегралов. Примеры. Найти объём тетраэдра с вершинами (0,0,0), (1,0,0), (1,1,0), (1,1,1).
Приложения кратных интегралов. Вычисление площадей фигур и объёмов тел.
Вывод формулы площади поверхности.
Площадь каждого такого параллелограмма вычисляется с помощью векторного произведения: *** Вывод формулы площади явно заданной поверхности:
§ 2. Замена переменных в кратных интегралах. Полярные координаты на плоскости. Вывести формулы перехода к полярным координатам на плоскости: Определитель Якоби: При замене двух старых на две новые переменные в плоскости, существует уже 4 различных частных производных, и из них можно образовать матрицу 2-го порядка. Её определитель: На этот определитель нужно домножить в кратном интеграле после пересчёта всех переменных. Геометрический смысл определителя Якоби - правильный учёт искажений (деформаций). Чертёж - слева в плоскости параметров
При одном и том же угле поворота, площади секторов, находящихся дальше от центра, будут больше, чем те, которые ближе к центру. Если бы не умножали на определитель Якоби, то влияние значений функции в этих секторах было бы одинаковым, так как диапазон изменений угла для них один и тот же. Определитель Якоби в кратных интегралах имеет точно такой же смысл, как например дополнительный множитель, появляющийся при заменен переменной в неопределённом или определённом интеграле. Так, если
*** Вывести формулы перехода к полярным координатам и вычислить их определитель Якоби.
ЛЕКЦИЯ 9 - 08.04.2014 Продолжение - тема полярные координаты. Пример: Вычислить интеграл Решение.
Пример: Доказать формулу площади круга с помощью полярных координат.
Цилиндрические и сферические координаты в пространстве. Существует два различных обобщения полярных координат для трёхмерного пространства. Вывод формул перехода к цилиндрическим координатам в пространстве:
*** Вывести формулы перехода к цилиндрическим координатам и их определитель Якоби.
Пример: доказать формулу объёма конуса
*** Вывести формулы перехода к сферическим координатам. Вывести формулы перехода к сферическим координатам в пространстве:
Вычислить определитель Якоби
Пример: доказать формулу объёма шара с помощью тройного интеграла и сферических координат.
§ 3. Криволинейные и поверхностные интегралы от векторных функций. Определение. Свойства, геометрический и физический смысл. Работа силы по перемещению точки по кривой,
*** Вывод формул вычисления работы поля для параметрически заданной кривой.
Пример (задача). Вычислить работу поля F = (xy,x+y) по участку кубической параболы от (0,0) до (1,1). Решение: Ответ 29/20. Поток поля через поверхность. Вывод формулы для явно заданной поверхности. ЛЕКЦИЯ 10 - 15.04.2014 § 4. Элементы теории поля. Определение векторного поля. Векторная функция, отображающая
Градиент скалярной функции - векторная функция:
Пример:
Потенциальное поле: Если существует такая U(x,y,z), что
Свойство. Если U - потенциал, то U+C - тоже потенциал. Доказательство:
*** Теорема 1. Поле F потенциально
ДОКАЗАТЕЛЬСТВО.
потому что Но (!!!) эти смешанные частные производные 2-го порядка совпадают, значит, Аналогично Итак,
Определение. Дивергенция векторного поля.
Определение Ротор векторного поля. rot(F) = Куда направлен ротор (чертёж на доске для векторного поля (-y,x,0) ). Определение. Если ротор = 0 то поле называется безвихревым.
*** Следствие. Векторное поле F потенциально ДОКАЗАТЕЛЬСТВО.
Следствие (для плоского поля). Векторное поле в R2 потенциально
Определение. Работа векторного поля при перемещении точки по замкнутому контуру называется циркуляцией. Обозначение:
*** ЛЕММА. Криволинейный интеграл 2 рода от F не зависит от пути ДОКАЗАТЕЛЬСТВО.
Необходимость. Если Но так как объединение 2 частей в замкнутый контур
Достаточность. Если Возникают 2 части, и
*** Теорема 2. Поле F потенциально Примечание. Потенциал в точке А вычисляется как U(А)-U(A0), где A0 - начальная точка, как правило (0,0,0).
ДОКАЗАТЕЛЬСТВО. Необходимость. Если поле потенциально то а тогда в интеграле Достаточность. Если криволинейный интеграл для поля (P,Q,R) не зависит от пути, возьмём начальную точку, например начало координат (0,0,0). Введём скалярную функцию U(x,y,z) равную работе поля от (0,0,0) до точки А(x,y,z). То есть
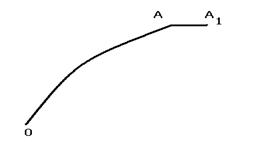
Составим путь из дуги от 0 до А и дополнительного маленького горизонтального отрезка вдоль оси Ох. Интеграл от 0 до А равен U(А). Интеграл от 0 до А1 равен U(А1). Их координаты А (x,y,z) А1 (x+∆x,y,z) .
при этом y, z константы, то есть dy = 0, dz = 0.
То есть Аналогично
Алгоритм нахождения потенциала, пример. Пример.
Итак, эта матрица симметрична, значит, поле потенциально. Теперь ищем потенциал. Для этого вычислим криволинецный интеграл от точки (0,0) до произвольной точки (x,y). Так как он не зависит от пути, выберем для простоты ломаную, так чтобы отрезки были вдоль осей
В пространстве было бы Интегральные формулы. Формула Грина. Пример вычисления работы по единичной окружности от поля F = (-y,x) без формулы и по формуле Грина.
Формула Стокса Формула Остроградского-Гаусса.
Задача в 3-мерном пространстве. Пример. Доказать, что поле
Решение. Найдём производную матрицу и докажем её симметричность.
ЛЕКЦИЯ 11 - 22.04.2014
Глава 5. Дифференциальные уравнения
§ 1. Дифференциальные уравнения 1-го порядка.
1) Уравнения с разделяющимися переменными. Примеры: 2) Однородные (по степени) уравнения *** Доказать, что замена
3) Линейные однородные и неоднородные. *** Метод Лагранжа для неоднородных линейных уравнений 1 порядка. Пример. 4) Уравнения Бернулли. *** Обосновать метод сведения уравнения Бернулли к линейному уравнению с помощью замены ЛЕКЦИЯ 12 - 29.04.2014 5) Уравнения с разделяющимися переменными.
§ 2. Дифференциальные уравнения n-го порядка. Методы понижения порядка. Случай 1) если в уравнении не содержатся младшие порядки производных, то есть тип уравнения тогда замена y(k)=z, при этом y(k+1)=z’,... Доказать, что замена Пример.
или
Случай 2) если в уравнении содержатся все порядки производных, но нет х, то есть тип уравнения
замена y’=p(y) *** Вывести и обосновать замену, доказать что
Пример:
Линейное уравнение высшего порядка.
*** Теорема 1. Доказать, что
Пример
*** Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.
ЛЕКЦИЯ 13 - 6.05.2014
*** Теорема 3. (Теорема о наложении решений). Если y1 - решение линейного неоднородного дифф.уравнения с правой частью b1(x), а y2 - решение такого же дифф.уравнения, но с правой частью b2(x), то линейная комбинация Ay1 + By2 является решением уравнения с правой частью Ab1(x) + Bb2(x).
*** Следствие. Сумма решений линейного неоднородного и соответствующего однородного дифференциального уравнения является решением неоднородного уравнения.
Определение линейной зависимости и независимости. Определитель Вронского. Примеры. x,2x x,x2.
*** Теорема 4. Доказать, что
Определение ФСР. Теорема 5. Существует ровно n линейно-независимых решений линейного однородного дифф. уравнения порядка n, всякое решение есть их линейная комбинация. Определение. Система из n решений, указанная в этой теореме, называется ФСР (фундаментальной системой решений) линейного однородного дифф. уравнения.
3 случая: случай 1 - все характеристические корни действительные и различные ( док, что система Пример Пример
случай 2 - все характеристические корни действительные, но среди них есть кратные
*** Теорема 6. Если r=0 является характеристическим корнем кратности k, то функции 1, x, x2, x3,...,xk-1 принадлежат ФСР однородного дифференциального уравнения.
Система
Пример.
случай 3 - есть комплексные характеристические корни. Если корень a+bi, то в ФСР входят две функции: Пример.
Метод Лагранжа для линейного неоднородного уравнения порядка n, построение системы для неизвестных. Система, из которой находятся неизвестные функции:
Пример. Решение методом Лагранжа уравнения Сначала решается соответствующее однородное уравнение Его характеристическое уравнение это Далее вместо констант ставим неизвестные функции, то есть решение неоднородного ищем в виде
Решая её методом Гаусса, находим производные, а затем и сами функции и подставляем их в выражение
ЛЕКЦИЯ 14 - 13.05.2014 Метод неопределённых коэффициентов для неоднородного уравнения.
Пример.
Пример. Системы дифференциальных уравнений. *** Доказать, что ЛЕКЦИЯ 15 - 20.05.2014 Пример. Однородная система Метод Лагранжа для неоднородных систем. Пример. Неоднородная система.
§ 5. Дифф. уравнения в частных производных. Волновое уравнение: Уравнение диффузии: Граничные условия: Метод Фурье разделения переменных. Пусть функция представима в виде произведения двух функций от каждом переменной: Тогда Доказывается, что при
ЛЕКЦИЯ 16 - 27.05.2014 Метод Фурье разделение переменных: завершение. Комплексные числа, степени и корни, тригонометрическая и показательная форма и действия с помощью них. Понятие комплексного числа и основы действий с ними. Действительная, мнимая часть. Тригонометрическая и показательная форма. Доказательство формулы Эйлера Формула Муавра для возведения в степень. Примеры: ЛЕКЦИЯ 17 - 3.06.2014 Комплексные числа Примеры: Корни из комплексного числа. Доказательство того, что при разнице углов Формула корней степени n . Примеры по этой формуле.
семестр вопросы к экзамену (доказательства из конспекта лекций) (как правило, помечены там знаком *** ) |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 148. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


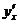 для неявно заданной кривой
для неявно заданной кривой  :
: 
 ,
, 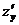 для неявно заданной поверхности
для неявно заданной поверхности 
 от
от 
 ,
,  ,
,  ,
,  ,
,  .
. ,
, 

 ,
, (выделение полного квадрата)
(выделение полного квадрата) (понижение порядка)
(понижение порядка) то есть прибавлять константу внутри знака дифференциала, от этого ничего не изменится, но структуру так можно преобразовать. Ведь дифференциал от константы равен 0.
то есть прибавлять константу внутри знака дифференциала, от этого ничего не изменится, но структуру так можно преобразовать. Ведь дифференциал от константы равен 0.


 ,
,  ,
,  .
. .
. для интегралов
для интегралов  .
. .
.



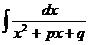



 .
. .
. .
. , замена
, замена  , тогда
, тогда  ,
,  .
. ,
,  .
. 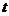 , например:
, например:  . Пример
. Пример  =
=  =
=  .
. в интеграле
в интеграле  сводит интеграл к рациональной дроби от
сводит интеграл к рациональной дроби от  .
. , при этом:
, при этом:  ,
,  ,
,  .
.
 , при этом:
, при этом:  ,
,  ,
,  .
.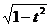 .
. .
. , тогда
, тогда  ,
,  ,
,  ,
,  .
. =
= 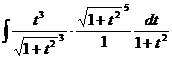 =
=  =
= 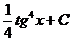 .
.
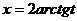 ,
,  ,
, 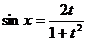 ,
,  .
.  .
. ,
,  ,
,  сводящихся к тригонометрическим.
сводящихся к тригонометрическим. .
.  (или
(или  ). При этом
). При этом  ,
,  .
. =
=  .
. 
 .
.  (или
(или  ). При этом
). При этом  ,
, 
 .
. 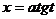 (или
(или  ). При этом
). При этом  ,
, 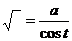 .
. ,
,  ,
, ,
, ,
, то
то  ,
, то
то 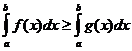 ,
, ,
, то
то  ,
, , что
, что 
 , что
, что 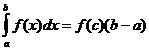 .
. является первообразной для
является первообразной для 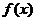 .
.  .
.  .
. .
. .
.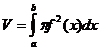 ,
,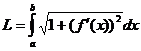 .
. .
.  .
.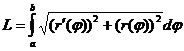 .
. или
или  .
.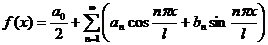 .
.
 ,
, 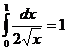 .
. сходится при
сходится при  , а несобственный интеграл 2-го рода
, а несобственный интеграл 2-го рода  сходится при
сходится при 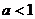 .
. ,
,  ,
,  .
. сходится
сходится  первообразная имеет конечный предел
первообразная имеет конечный предел  .
.
 .
.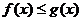 и сходится интеграл
и сходится интеграл  , то сходится и интеграл
, то сходится и интеграл 
 , причём константа C отлична от 0 и от
, причём константа C отлична от 0 и от  , то интеграл
, то интеграл 
 .
.
 ,
, 
 ,
, 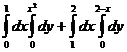


 , а именно векторов (1,0,f ‘x), (0,1,f ‘y).
, а именно векторов (1,0,f ‘x), (0,1,f ‘y). .
. .
.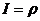 .
. =
= 
 =
=  .
.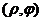 , справа в плоскости
, справа в плоскости  .
.
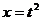 , то при замене пишем
, то при замене пишем 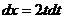 . Множитель
. Множитель  фактически и является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.
фактически и является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом. где D -
где D -  часть круга единичного радиуса в первой четверти плоскости.
часть круга единичного радиуса в первой четверти плоскости. =
=  =
= =
=  =
=  =
= =
= 
 =
=  =
=  =
=  =
= 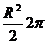 =
=  .
. .
. .
.
 .
. .
. ,
,  ,
, 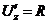
 - тогда
- тогда  .
. называется потенциалом поля
называется потенциалом поля 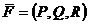
 ,
,  ,
, 
 .
.
 ,
, 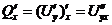 ,
, =
=  .
. =
=  . Аналогично
. Аналогично  =
=  .
. и матрица симметрична.
и матрица симметрична. (сумма элементов главной диагонали производной матрицы).
(сумма элементов главной диагонали производной матрицы). =
=  .
. =
=  .
. .
. или
или 

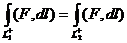 то
то  то
то  .
. , тогда и получается
, тогда и получается .
. , разобъём контур на 2 части какими-нибудь 2 точками А,В.
, разобъём контур на 2 части какими-нибудь 2 точками А,В. , значит
, значит 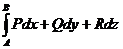 получится
получится  а по формуле полного дифференциала это
а по формуле полного дифференциала это  но ведь первообразная от производной - это сама функция U, тогда работа поля
но ведь первообразная от производной - это сама функция U, тогда работа поля  =
=  то есть зависит только от начальной и конечной точки.
то есть зависит только от начальной и конечной точки. .
.
 =
=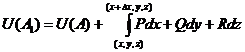 но в интеграле по отрезку АА1 меняется только x,
но в интеграле по отрезку АА1 меняется только x, для некоторой промежуточной точки с, где достигается среднее значение. Тогда
для некоторой промежуточной точки с, где достигается среднее значение. Тогда  ,
,  =
= 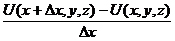 . Но точка с тоже стремится к х при ∆x →0.
. Но точка с тоже стремится к х при ∆x →0. . Итак,
. Итак,  . Доказать, что поле потенциально, и найти потенциал.
. Доказать, что поле потенциально, и найти потенциал. =
=  .
. =
=  =
=  =
=  .
. .
. .
. .
. .
. потенциально и найти его потенциал.
потенциально и найти его потенциал. =
= 
 ,
,  ,
, 

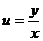 сводит однородное уравнение к уравнению с разделяющимися переменными.
сводит однородное уравнение к уравнению с разделяющимися переменными.

 понижает порядок уравнения
понижает порядок уравнения 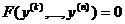 .
. Варианты начальных условий:
Варианты начальных условий: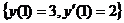 (условия Коши)
(условия Коши)  (в двух различных точках)
(в двух различных точках)
 . Доказать, что замена
. Доказать, что замена  понижает порядок уравнения, в котором отсутствует
понижает порядок уравнения, в котором отсутствует  , то есть уравнения вида
, то есть уравнения вида  .
. (уравнение колебаний) решить этим методом.
(уравнение колебаний) решить этим методом. - неоднородное.
- неоднородное.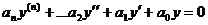 - однородное.
- однородное. является решением
является решением  .
. система функций линейно-зависима.
система функций линейно-зависима. линейно независима. )
линейно независима. ) .
. .
. линейно независима и входит в ФСР однородного уравнения, если 0 есть корень кратности k.
линейно независима и входит в ФСР однородного уравнения, если 0 есть корень кратности k. входит в ФСР однородного уравнения, если r есть корень кр-сти k.
входит в ФСР однородного уравнения, если r есть корень кр-сти k. .
. и
и  .
.
 .
. , корни равны 1 и 2, общее решение однородного
, корни равны 1 и 2, общее решение однородного  .
. . Для того, чтобы найти неизвестные функции, строим систему:
. Для того, чтобы найти неизвестные функции, строим систему:
 .
. совпадает с корнем кратности 2, ответ
совпадает с корнем кратности 2, ответ 
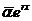 явл. реш. лин. однородной системы дифф. ур
явл. реш. лин. однородной системы дифф. ур  собст. вектор,
собст. вектор,  собст число.
собст число. . Отв.
. Отв.  .
. отв
отв  .
.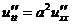

 .
. .
.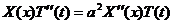 , следовательно,
, следовательно,  . Поскольку в разных частях равенства получились функции от разных переменных, то единственная возможность их равенства - они являются константами. Поэтому
. Поскольку в разных частях равенства получились функции от разных переменных, то единственная возможность их равенства - они являются константами. Поэтому  .
. решение (с учётом условия
решение (с учётом условия  ) только нулевое, остаётся лишь
) только нулевое, остаётся лишь  . Обозначим
. Обозначим  ,
,  , характеристические корни
, характеристические корни  .
. . Учитывая
. Учитывая  ,
,  ,
,  ,
,  .
. .
. ,
,  ,
,  ,
,  .
. ,
, 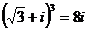 ,
,  .
. , n -я степень чисел одинакова.
, n -я степень чисел одинакова. .
.