Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
К ВЫПОЛНЕНИЮ ОСНОВНОЙ ЧАСТИ ИНДИВИДУАЛЬНОГО ЗАДАНИЯМЕТОДИЧЕСКИЕ УКАЗАНИЯ При выполнении данного задания необходимо знать основные правила интегрирования и таблицу простейших неопределенных интегралов I. При решении этого примера используется свойство И подбор соответствующей подстановки, приводящей исходный интеграл к табличному интегралу, а именно
Пример. Вычислить интеграл
Проведем отдельно вычисление каждого интеграла
Следовательно,
2. Если U(x) и V(x) – дифференцируемые функции, то имеет место формула интегрирования по частям
При использовании формулы интегрирования по частям в подынтегральном выражении важно уметь правильно выделить функцию U и дифференциал dV, так чтобы в правой части равенства интеграл
а для интегралов Иногда, чтобы свести исходный интеграл к вычислению некоторого табличного интеграла, приходится применять формулу интегрирования по частям несколько раз. Пример. Вычислить интеграл. Вычислить интеграл.
3. В этот пример включены интегралы вида
При решении этих интегралов если m не равно 0 , то из числителя выделяется производная 2ax+bквадратного трехчлена и интеграл разбивается на сумму двух интегралов.
Аналогично
Таким образом исходные интегралы сводятся к вычислению интегралов
Для этих интегралов целесообразно использовать подстановку 2ax+b=t. Тогда 
Следовательно
Пример. Найти интеграл
4. Интегрирование произвольной рациональной дроби
С действительными коэффициентами в общем случае производится следующим образом. Если исходная дробь Pm(x)/Q n (x)неправильная, то следует предварительно выделить в этой дроби целую часть, т.е. представить ее в виде
Где Выделение целой части у неправильной рациональной дроби производится делением числителя на знаменатель. Таким образом, интегрирование произвольной рационально дроби сводится к интегрированию многочлена и правильной рациональной дроби. Интегрирование правильной рациональной дроби
Где k =2, 3, ……; A, B, p, q - действительные постоянные причем Количество простых дробей и их вид определяется множителями, на которые может быть разложен знаменатель
То
Коэффициенты A, B, C1, C2, C3, A1, B1, A2, B2 определяются методом неопределённых коэффициентов. Пример. Найти Дробь
Так как дробь, стоящая справа, равна дроби слева, то числители у них тождественно равны, т.е.
Приравнивая коэффициенты при одинаковых степенях ч, получим систему:
Следовательно,
5. При вычислении интегралов, содержащих тригонометрические функции, можно выделить следующие интегралы: А) Интеграл вида Если m=2k+1– нечетное положительное то :
Если n=2k+1 – нечетное положительное число, то аналогично имеем
Если mиn – четные положительные числа, то степени понижаются посредством перехода к двойному аргументу с помощью тригонометрических формул
Б) Интегралы вида
Функция, получившаяся в подынтегральном выражении, является дробно-рациональной функцией и к ней применимы известные приемы: В) интегралы вида Если Здесь
Г) интегралы вида
Пример. Найти интеграл
6. Интегралы вида
Где R– рациональная функция относительно x, а m,n,p,q,…- целые числа, вычисляются с помощью подстановки
Пример. Найти интеграл
Так как подынтегральная функция является неправильной рациональной дробью, то необходимо выделить целую часть , т.е. поделить числитель на знаменатель. В результате деления получим
7. При вычислении определенного интеграла используется формула Ньютона-Лейбница
Отыскание первообразной F(x) осуществляется теми же методами, что и при вычислении неопределенного интеграла. Следует отметить, что замена переменной в определенном интеграле влечет за собой изменение пределов интегрирования. Действительно
Новые пределы интегрирования α и β, при выбранной замене Пример. Вычислить определенный интеграл
8. При решении данного примера следует пользоваться указаниями, относящимися ко второму примеру и формулой интегрирования по частям
Где функции u(x) и v(x) непрерывно дифференцируемые на отрезке [a,b]. Пример. Применяя формулу интегрирования по частям, вычислить интеграл
+ 9. К несобственным интегралам 1-го рода относятся интегралы с бесконечными пределами. Если функция f(x) непрерывна на промежутке [a;∞], то по определению
Если существует конечный предел в правой части данного равенства, то несобственный интеграл 1-го рода называется сходящимся, если этот предел не существует, то – расходящимся. Аналогично определяются интегралы вида:
Пример. Вычислить несобственный интеграл (или установить его расходимость )
Интеграл сходится. 10. К несобственным интегралам 2-го рода относятся интегралы от неограниченных функций. Если функция f(x) не ограничена в окрестности точки спринадлежит [a,b]и непрерывна на промежутках [a; c [ и ] c; b ], то по определению
Если пределы в правой части данного равенства существуют и конечны, то несобственный интеграл 2-го рода называется сходящимся, в противном случае расходящимся. Если точка С совпадает с одним из концов отрезка [a,b], то определение упрощается а именно
Пример. Вычислить несобственный интеграл (или установить его расходимость)
Следовательно, интеграл расходится.
II. Если плоская фигура в декартовой системе координат Рис. 1 Рис. 2 Ограничена двумя непрерывными кривыми
Для плоской фигуры, представленной на Рис. 2, целесообразней использовать формулу
Решение данной задачи следует начинать с изображения заданных кривых на плоскости, т.е. уточнения вида плоской фигуры, площадь которой следует найти. Это поможет уточнить выбор соответствующей формулы, найти пределы интегрирования к функции
Пример.. Найти площадь фигуры, ограниченной кривыми
Изобразив графики параболы и прямой, видим, что
Решение данной задачи необходимо начать с выяснения области определения заданной функции. Так как для полярных координат r >= 0 , то имеем Из представленного графика видно, что
12. Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой y=f(x), осью ОХ и двумя прямыми x=aи x=b, вокруг оси ОХ выражается формулой
Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой x=ϕ(y),осью ОУ и двумя прямыми y=c, y=d вокруг оси OУвыражается формулой
В более общем случае объем тела, образованного вращением фигуры, ограниченной кривыми
Соответственно, для фигуры, ограниченной кривыми
Решение данной задачи, как и в случае вычисления площади плоской фигуры, следует начинать с изображения графиков соответствующих кривых. Пример. Найти объем тела, образованного вращением фигуры, ограниченной параболой y=x2+2xи прямой y=0вокруг оси ОХ и вокруг оси ОУ. a)В случае вращения вокруг оси ОХимеем
б)Если рассматриваемую фигуру вращать вокруг оси ОУ , то для вычисления объема получившегося тела вращения нужно предварительно найти
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 159. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

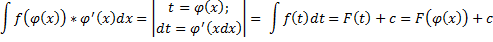


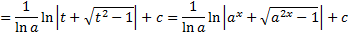
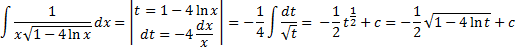


 был проще интеграла
был проще интеграла  . Так например если в подынтегральном выражении содержит многочлен
. Так например если в подынтегральном выражении содержит многочлен  , то в выборе U и dV может быть рекомендовано следующее: для интегралов вида
, то в выборе U и dV может быть рекомендовано следующее: для интегралов вида следует положить
следует положить 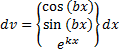 ,
, 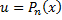 ,
,  следует принять
следует принять  ,
, 






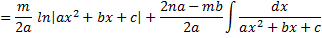



 , откуда
, откуда и
и 




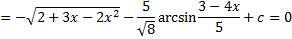

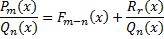
 – многочлен степени m-n >=0, а
– многочлен степени m-n >=0, а  - многочлен степени r < n, т.е. дробь
- многочлен степени r < n, т.е. дробь 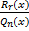 - правильная.
- правильная. , где r < n, осуществляется разложением дроби в сумму простейших дробей вида
, где r < n, осуществляется разложением дроби в сумму простейших дробей вида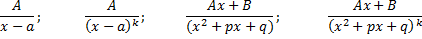



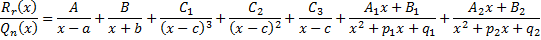

 – правильная, ее разложение в сумму простейших дробей имеет вид:
– правильная, ее разложение в сумму простейших дробей имеет вид:

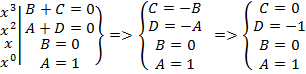

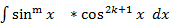 где m и n – целые числа
где m и n – целые числа


 , где R- рациональная функция, вычисляются с помощью подстановки tg x=tили x=arctgt
, где R- рациональная функция, вычисляются с помощью подстановки tg x=tили x=arctgt
 где R- рациональная функция.
где R- рациональная функция. т.е. sin x, cos x содержатся только в четных степенях, то используется подстановка tgx=t;
т.е. sin x, cos x содержатся только в четных степенях, то используется подстановка tgx=t;
 ,
,  преобразуются к табличным с помощью формул
преобразуются к табличным с помощью формул


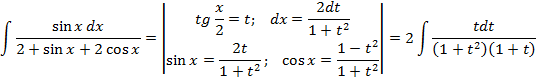














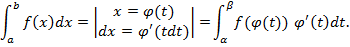
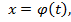 находятся из уравнений
находятся из уравнений 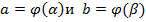 , где
, где  и
и  должны быть определены и непрерывны на [α, β].
должны быть определены и непрерывны на [α, β].






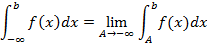
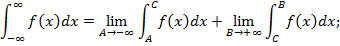








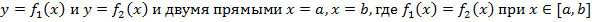 то площадь S определяется формулой
то площадь S определяется формулой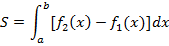

 , соответствующим значениям
, соответствующим значениям  , определяются интегралом
, определяются интегралом


 .
. 
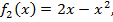 a=0; b=3;
a=0; b=3;  Следовательно,
Следовательно, 

 , что равносильно
, что равносильно  , или
, или 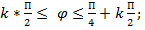 где k=0,1,2,3…
где k=0,1,2,3…


 (причем
(причем  ) и прямыми x=a, x=b, вокруг оси ОХ равен
) и прямыми x=a, x=b, вокруг оси ОХ равен
 (
(  ), и прямыми y=c, y=dвращающейся вокруг оси ОУ объем тела определяется формулой
), и прямыми y=c, y=dвращающейся вокруг оси ОУ объем тела определяется формулой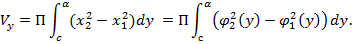

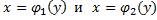 . Рассматривая соотношение
. Рассматривая соотношение как уравнение относительно х, находим
как уравнение относительно х, находим , где
, где  ;
;