
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие подпрограммы. Способы реализации подпрограмм на ПаскалеСтр 1 из 2Следующая ⇒ Создание и использование функций пользователя План. 1. Понятие подпрограммы. Способы реализации подпрограмм на Паскале 2. Описание и использование функций Понятие подпрограммы. Способы реализации подпрограмм на Паскале В практике программирования часто встречаются алгоритмы, в которых повторяются фрагменты, одинаковые по выполняемым действиям и различные только значениями обрабатываемых данных.
 
Площадь четырехугольника в данном случае можно определить как сумму площадей треугольников ABD и BCD, вычисленных по формуле Герона Поскольку здесь дважды необходимо вычислить значение площади треугольника, то очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения площади треугольника по трем сторонам. Эта задача решается с помощью формулы Герона. Для более эффективной обработки подобных алгоритмов вводится понятие подпрограммы. Подпрограмма – это группа операторов, оформленная в виде самостоятельной программной единицы со своими входными и выходными данными и именем. Подпрограмма вызывается из основной программы, получает из нее входные данные, выполняет свою группу операторов и возвращает управление в точку вызова (возможно с данными). При выполнении подпрограммы работа текущей программы приостанавливается до момента возврата в нее.  Использование подпрограмм улучшает структуру программы, делает ее более наглядной и понятной, облегчает процесс проектирования, разработки и отладки. При использовании в алгоритме подпрограммы (вспомогательного алгоритма) сама подпрограмма оформляется в виде отдельного алгоритма, а вызов ее из основного алгоритма оформляется блоком подпрограммы. Так для поставленной выше задачи алгоритм решения примет вид (слева – основной алгоритм, справа – вспомогательный):
Схема вспомогательного алгоритма (подпрограммы) начинается блоком «начало», в котором указывается имя подпрограммы и список входных параметров (данных), необходимых для работы вспомогательного алгоритма, а заканчивается блоком «конец», в котором указывается вычисленное им значение, которое возвращается в основной алгоритм. В основном алгоритме происходит обращение к вспомогательному алгоритму, которое оформляется в блоке вспомогательного алгоритма. В языке Паскаль подпрограммы реализуются в виде процедур и функций, которые вводятся в программу с помощью своего описания в соответствующих разделах. Заголовок подпрограммы начинается со слова procedure или function, за которым указывается имя подпрограммы и список формальных параметров – перечень имен для обозначения исходных данных и результатов работы с указанием их типа. В подпрограмме могут использоваться: 1) все имена, объявленные в программе до описания данной подпрограммы; 2) имена, объявленные в самой подпрограмме, включая формальные параметры. Имена, объявленные в подпрограмме называются локальными, а объявленные в программе и объемлющих подпрограммах – глобальными. При использовании подпрограммы-функции важно помнить: 1. Алгоритм, оформленный в виде функции имеет единственный скалярный результат. 2. Вызов функции осуществляется путем размещения ее имени со списком фактических параметров. Во время обращения к подпрограмме происходит замена формальных параметров фактическими параметрами – величинами, определенными в вызывающей программе. Поэтому важно, чтобы фактические параметры соответствовали формальным параметрам по количеству, порядку следования и по типу. Пример: пусть требуется определить наибольший общий делитель трех величин x, y, z. Идея решения состоит в следующем математическом факте: если х, у, z — три натуральных числа, то НОД(х, у, z) = НОД(НОД(х, у), z). Иначе говоря, нужно найти НОД двух величин, а затем НОД полученного значения и третьего числа. Очевидно, что вспомогательным алгоритмом для решения поставленной задачи является алгоритм получения наибольшего общего делителя двух чисел. Эта задача решается с помощью известного алгоритма Евклида. Для поставленной задачи алгоритм решения примет вид (слева – основной алгоритм, справа – вспомогательный):
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 261. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
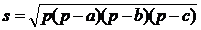 , где
, где  – полупериметр, a, b, c – длины сторон.
– полупериметр, a, b, c – длины сторон.
