
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Доказательство примитивной рекурсивности функцийВведение.
Эти выводы верны в силу своей формы, независимо от содержания, независимо от того истинны или ложны взятые по себе посылки и заключения. Систематическая формализация и каталогизация правильных способов рассуждений – одна из основных задач логики. Если при этом применяется математический аппарат и исследования посвящены в первую очередь изучению математических рассуждений, то эта логика является математической логикой (формальной логикой). Данное определение не является строгим (точным) определением. Чтобы понять предмет и метод математической логики лучше всего приняться заее изучение. Математическая логика начала формироваться давно. Зарождение ее идей и методов происходило в Древней Греции, Древней Индии и Древнем Китае примерно с VI в. до н. э. Уже в этот период ученые пытались расположить цепь математических доказательств в такую цепочку, чтобы переход от одного звена к другому не оставлял сомнений и завоевал всеобщее признание. Уже в самых ранних дошедших до нас рукописях «канон» математического стиля изложения прочно установлен. Впоследствии он получает окончательное завершение у великих классиков: Аристотеля, Евклида, Архимеда. Принципиальное значение математической логики – обоснование математики (анализ основ математики). Прикладное значение математической логики в настоящее время очень велико. Математическая логика применяется для следующих целей: • анализа и синтеза (построения) цифровых вычислительных машин и других дискретных автоматов, в том числе и интеллектуальных систем;  • анализа и синтеза формальных и машинных языков, для анализа естественного языка; • анализа и формализации интуитивного понятия вычислимости; • выяснения существования механических процедур для решения задач определённого типа; • анализа проблем сложности вычислений. Также математическая логика оказалась тесно связанной и с рядом вопросов лингвистики, экономики, психологии и философии. Логические сети
Пусть имеется конечное множество А:
а Логическую сеть можно представить в виде графа, вершины которого имеют номера из множества А и соответствуют логическим функциям из F, а дуги определяются элементами из Пример
f1f1
f1
Т. о., можно сказать, что логическая сеть представляется орграфом с перенумерованными вершинами, которые соответствуют логическим функциям из заданного множества. Рассмотрим теперь множество Например, для рассматриваемой логической сети можно определить
f1f1
f1
Потребуем, чтобы соответствующий граф не содержал циклов и являлся бы упорядоченным, т. е. для любой дуги ( i, j ) выполнялось бы i<j . Такая сеть называется упорядоченной или сетью без обратных связей. Потребуем также, чтобы функция Упорядоченная и правильная логическая сеть называется регулярной (РЛС). Их мы в дальнейшем и будем рассматривать. Введем, наконец, множество выходов
и зададим отображение подмножеств Например, для рассматриваемой сети зададим
Если после введения отображения Полученная в итоге сеть называется логическим многополюсником или конечным автоматом без памяти. Если при этом множество X содержит n элементов, а Y – k элементов, то мы имеем логический (n, k) – полюсник. Например, рассматриваемая нами сеть является логическим (2, 2) – полюсником. Графическое представление логической сети называется ее схемой.
Анализ логических сетей
Пусть функции, входящие в многоканальник (( n, k ) – полюсник ) образуют следующую систему.
Эта система называется системой собственных функций ( n, k ) – полюсника. Анализ логической сети сводится к написанию системы собственных функций для заданной схемы логической сети. Пример
Анализ схемы дает однозначное написание собственных функций. Если при этом пользоваться скобочной формой записи, то система собственных функций отражает и структуру схемы. В дальнейшем будем использовать стандартные обозначения для наиболее часто встречающихся логических функций.
Практическая часть
Задание 1. Определить все логические следствия из посылок Решение. Образуем конъюнкцию посылок и найдем ее СКНФ:
Тогда следствиями являются
Задание 2. Определить все посылки, логическим следствием которых является формула Решение. Для конъюнкции Образуем всевозможные произведения с недостающими сомножителями:
Данная формула может логически следовать либо из самой себя, либо из тождественно ложной формулы.
Задание 3 Доказать истинность заключения дедуктивным методом и нарисовать граф вывода заключения: (A®B); (B®C); (C®D) |¾ (A®D). Решение. 1) 2) 3) 4) C 5)
Задание 4 Составить таблицу истинности. Доказать истинность заключения по методу резолюции и нарисовать граф вывода пустой резольвенты. (A®B); (B®C); (C®D) |¾ (A®D). Решение. Образуем конъюнкцию посылок, т.е. F= Для полученной формулы составим таблицу истинности.
Докажем истинность заключение по методу резолюций. 1) 2) 3) 4) 5) S={ 6) 7) 8) 9)
Задание 5 Найти формулы ПНФ и ССФ. "x(ù A(x)®$y(ù B(y)))®(B(y)®A(x))
Решение. ПНФ:
ССФ:
Доказательство примитивной рекурсивности функций Задание 6. Доказать примитивную рекурсивность функции Решение. Будем строить рекурсию по первой переменной. Применяем операцию примитивной рекурсии:
Построение машины Тьюринга Задание 7. Построить машину Тьюринга, вычисляющую функцию f (x) = 4x. Решение. Определим порядок вычисления значения этой функции машиной Тьюринга. Так как результат должен представлять массив из 4k -1 занятых ячеек, то где k = x +1 - число ячеек, занятых аргументом x, то вычисление организуем следующим образом. В ячейку, занятую аргументом x, вместо символа 1 записы-ваем пустой символ 0. в каждом таком случае символ 1 записы- вается в двух ячейках, представляющих результат. Этот резуль- тат формируем в виде массива ячеек, расположенных справа от массива ячеек, занятых аргументом x, через одну пустую ячейку. Когда вместо всех ячеек, занятых аргументом x, будут только пустые ячейки, в новом массиве занятых ячеек удаляется одна ячейка с символом 1. Программа работы машины Тьюринга, вычисляющая функцию f (x) = 4x , имеет вид: 1q1 ® 0q2R - удалена одна занятая ячейка аргумента. 1q2 ®1q2R - читаются занятые ячейки аргумента. 0q2 ® 0q3R - найдена разделяющая пустая ячейка. 1q3 ®1q3R- читаются занятые ячейки результата. 0q3 ®1q4R - заполнена одна пустая ячейка результата. 0 q4 ®1q5L - заполнена вторая ячейка результата. 1q5 ®1q5L - просматриваются в обратном порядке заня-тые ячейки результата. 0q5 ® 0q6L - найдена пустая разделяющая ячейка. 0q6 ® 0q7R - найдена вторая пустая ячейка. 0q7 ® 0q8R - снова читается пустая разделительная ячей- ка. 1q8 ® 0q0R - удаляется один занятый символ. Конец. 1q6 ®1q9L - найдена занятая ячейка аргумента. 1q9 ®1q9L - просматриваются в обратном порядке заня-тые ячейки аргумента. 0q9 ® 0q1R - найдена пустая ячейка перед занятыми ячей-ками аргумента
Заключение Математическая логика является наукой о законах математического мышления. Применение математики к логике позволило представить логические теории в новой удобной форме и применить вычислительный аппарат к решению задач, малодоступных человеческому мышлению, и это, конечно, расширило область логических исследований. Сфера применения математической логики очень широка. С каждым годом растет глубокое проникновение идей и методов математической логики в информатику, вычислительную математику, лингвистику, философию. Мощным импульсом для развития и расширения области применения математической логики стало появление электронно-вычислительных машин. Оказалось, что в рамках математической логики уже есть готовый аппарат для проектирования вычислительной техники. Методы и понятия математической логики является основой, ядром интеллектуальных информационных систем. Средства математической логики стали эффективным рабочим инструментом для специалистов многих отраслей науки и техники. Математическую логику необходимо знать всем специалистам, независимо в какой среде он работает (будь то инженер, преподаватель, юрист или просто-врач). Список литературы 1. Васильев Н. А. Воображаемая логика. Избранные труды. - М.: Наука. 1989; - стр. 94-123. 2. Кулик Б.А. Основные принципы философии здравого смысла (познавательный аспект) // Новости искусственного интеллекта, 1996, No 3, с. 7-92. 3. Кулик Б.А. Логические основы здравого смысла / Под редакцией Д.А. Поспелова. - СПб, Политехника, 1997. 131 с. 4. Кулик Б.А. Логика здравого смысла. - Здравый смысл, 1997, No 1(5), с. 44 - 48. 5. Стяжкин Н. И. Формирование математической логики. М.: Наука, 1967. 6. Соловьев А. Дискретная математика без формул. 2001// http://soloviev.nevod.ru/2001/dm/index.html
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 317. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 . Пусть
. Пусть  – множество логических функций. Тогда совокупность множеств А, В совместно с однозначным отображением множества А но F называется логической сетью.
– множество логических функций. Тогда совокупность множеств А, В совместно с однозначным отображением множества А но F называется логической сетью.

 1 6
1 6
 2
2
 f2 3 4
f2 3 4


 f3 f1
f3 f1 5
5 элементы которого назовем входами логической сети и зададим отображение некоторых подмножеств из X на некоторые элементы из А, т. е.
элементы которого назовем входами логической сети и зададим отображение некоторых подмножеств из X на некоторые элементы из А, т. е.  . Геометрической интерпретацией этого отображения являются дуги, входы сети и вершины графа.
. Геометрической интерпретацией этого отображения являются дуги, входы сети и вершины графа.


 x1
x1
 , соответствующая вершине графа с номером i, зависела от стольких аргументов, сколько дуг входит в данную вершину. Если это условие выполнено, то логическая сеть называется правильной.
, соответствующая вершине графа с номером i, зависела от стольких аргументов, сколько дуг входит в данную вершину. Если это условие выполнено, то логическая сеть называется правильной.
 на множество Y
на множество Y  Геометрически это отображение будет выглядеть как дуги направленные от вершин графа к выходам.
Геометрически это отображение будет выглядеть как дуги направленные от вершин графа к выходам.

 в графе останутся вершины, из которых не выходит ни одной дуги, то назовем их тупиковыми и исключим из сети, вместе со всеми инцидентными им дугами.
в графе останутся вершины, из которых не выходит ни одной дуги, то назовем их тупиковыми и исключим из сети, вместе со всеми инцидентными им дугами.



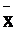
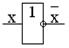

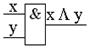


 y
y







 имеют по два входа, а отрицание константа 0 и константа 1 по одному.
имеют по два входа, а отрицание константа 0 и константа 1 по одному. ,
,  .
. .
. .
. .
.

 – посылка;
– посылка; – посылка;
– посылка; – по правилу 11 из 1) и 2);
– по правилу 11 из 1) и 2); – посылка;
– посылка; – по правилу 11 из 3) и 4).
– по правилу 11 из 3) и 4).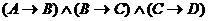 . Образуем импликацию от конъюнкции посылок до заключения:
. Образуем импликацию от конъюнкции посылок до заключения: .
.






 – посылка;
– посылка; – посылка;
– посылка; – посылка;
– посылка; – отрицание заключения;
– отрицание заключения; };
}; ;
; ;
; ;
; .
.


 .
.


 - произведение двух чисел
- произведение двух чисел