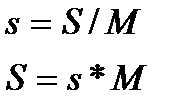Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
В) Плоская условная система прямоугольных координат ⇐ ПредыдущаяСтр 2 из 2 Элементы системы: -начало — произвольная точка -ось абсцисс (произвольно) - ось ординат (перпендикулярна к оси абсцисс) Обобщенный анализ плоской системы координат 1. Осями координат горизонтальная плоскость делится на 4 четверти.
2. В геодезии принята правая система прямоугольных координат (в отличие от принятой в математике левой декартовой системы) 3. Нумерация четвертей ведется по ходу стрелки часов, начиная с северо-восточной четверти, что позволяет использовать в геодезических вычислениях формулы тригонометрии без каких-либо изменений. Ось абсцисс 1 четверти ориентирована на север (0градусов).
5. Разность между проекциями двух точек на оси Х и У принято называть приращением координат и обозначать ( 6. Приращения координат имеют знаки (+), значение которых определяется координатными осями четвертей. 7. Если известны координаты одной точки, то координаты другой можно найти Хв =Ха +( Yв= Yа + ( 8. Система плоских координат имеет широкое применение в инженерной геодезии. Пространственные координаты. Геодезическая система координат. Элементы: - плоскость экватора, - ось вращения Земли перпендикулярная к экватору, -плоскость начального меридиана по международному соглашению-Гринвичский меридиан. Положение точки на поверхности эллипсоида определяется координатами: геодезической широтой В, геодезической долготой L.
 В —измеряется дугой геодезического меридиана от экватора до данной точки. — может быть северной и южной — может принимать значение от 0 до 90 градусов. Геодезическая долгота L —двугранный угол, составленный плоскостями начального меридиана и геодезического меридиана данной точки. L —измеряется дугой экватора, либо параллелями от Гринвичского меридиана до меридиана данной точки — может быть западной и восточной — может иметь значение от 0 до 180 градусов. Геодезическая система координат: — едина для всего земного шара — геодезическая сетка наносится на каждую топографическую карту — пользоваться геодезическими координатами при инженерных измерениях неудобно, потому что они даются в градусной мере — в геодезии наибольшее распространение получила система плоских прямоугольных координат, значения которых даны в линейной мере. Пространственная полярная система координат Элементы системы: — горизонтальная плоскость Q — центр координатной системы О — отвесная ось в центре корд. cистемы Z1 — начальная вертикальная плоскость Р0, Система находит применениев топографических съемках.
Масштабы,их виды,точность Масштаб —степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте. s/S — масштаб Виды масштабов: - численный (ч.м.) - графический Ч.м. —это правильная дробь, числитель которой есть единица, а знаменатель число, показывающее, во сколько раз горизонтальные проекции линий местности уменьшены на плане или карте. s/S = 1/S:s= 1/М, где М — знаменатель ч.м. Ч.М. — безразмерная величина, поэтому его можно использовать при измерениях в любых линейных мерах. Ч.М. применяют при определении длин линий на карте (плане) или на местности
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 307. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
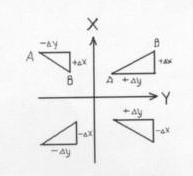 4. Координаты точек равны кратчайшим расстояниям от начала координат до проекции этих точек на оси Х и У.
4. Координаты точек равны кратчайшим расстояниям от начала координат до проекции этих точек на оси Х и У. х,
х,  у) (разность между координатами двух точек)
у) (разность между координатами двух точек)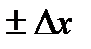 )
)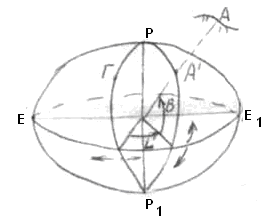 Геодезическая широта В —угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора.
Геодезическая широта В —угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора.