Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы решения задач целочисленного программированияДискретное программирование Задачи целочисленного линейного программирования 3.1.1 Задача о размещениях
Пусть имеются "m" пунктов, в которых могут размещаться предприятия, производящие некоторую единичную продукцию (станки, линии и т.д.). Кроме того заданы "n" пунктов потребления этой продукции с объемами потребления, равными соответственно b1, b2, ..., bn, а также матрицы транспортных затрат с = {сij}mхn. Здесь сij− затраты на транспортировку единицы продукции из производящего пункта "i" в потребляющий пункт "j". Задача состоит в таком размещении предприятий, определении их производственных мощностей и организации перевозок, чтобы суммарные затраты по производству и транспортировке были минимальны. Обозначим через хi − объем продукции в единицах, который необходимо производить в пункте "i", а через хij− количество единиц продукции, поставляемой из пункта "i" в пункт "j". Тогда затраты на производство продукции, если стоимость производства единицы продукции в пункте "i"−сi, будут равны Затраты на транспортировку произведенной продукции к потребителям
Вся задача формулируется так: Найти такие хi и хij, при которых
(суммарные затраты по производству и транспортировке минимальны), при условиях: 1) xi 2)
3)
4) хi, xij − принимают целочисленные значения. 3.1.2 Задача о назначениях 
Пусть имеется "n" единиц оборудования различных типов, которое требуется распределить между "n" предприятиями, имеющими различный уровень технической оснащенности. Обозначим сij - производительность "i"-го типа оборудования на "j''-м предприятии. Задача состоит в таком распределении оборудования (по одному на предприятие), которое обеспечит максимальную производительность. Определим неизвестные хij следующим образом:
Теперь задача может быть сформулирована следующим образом. Найти такие значения хij, чтобы производительность распределяемого оборудования была максимальной
при условиях: 1) 2) Отметим, что возможна задача о назначениях, в которой целью является минимизация. Конкретный пример будет приведен при иллюстрации алгоритма решения. 3.1.3 Задача о коммивояжере
Имеется "n" городов. Выезжая из одного, коммивояжер должен объехать все и вернуться в исходный город. В каждый город можно заезжать только один раз. Требуется найти минимальный замкнутый маршрут. Обозначим s= {sij }nxn - матрицу расстояний, хij - переменные, определим следующим образом:
Требуется минимизировать при условиях
(из каждого города коммивояжер выезжает только 1раз); (в каждый город коммивояжер въезжает 1 раз). Ui – Uj + nxij где Ui ,Uj − произвольные действительные числа. Последнее условие обеспечивает замкнутость маршрута и отсутствие петель. Методы решения задач целочисленного программирования 3.2.1 Метод отсечения Гомори
Запишем общую задачу целочисленного программирования в виде: найти максимум
в области, определенной условиями
хj >0 ,
хj− целые,
Метод отсечения Гомори состоит в следующем: а) решаем задачу линейного программирования (3.1) − (3.3); б) полученное оптимальное решение задачи (3.1) − (3.3), если оно существует, проверяем на целочисленность: − если все xj, j = − если задача линейного программирования решения не имеет, то не имеет решения и задача целочисленного программирования; − наконец, если хотя бы одна координата не удовлетворяет условию (3.4), то: в) строим дополнительное линейное ограничение, с помощью которого отсекается та часть допустимой области, определяемой условиями (3.2) − (3.3), в которой содержится оптимальное решение задачи линейного программирования (3.1) − (3.3), но нет ни одного допустимого решения, удовлетворяющего условию (3.4) и вновь выполняем пункт а) для задачи линейного программирования с дополнительным ограничением и т.д. Гомори показал, что при "k-ом" возвращении к решению задачи линейного программирования, "k-ое" дополнительное ограничение имеет вид: где [xi0], [xij] − целая часть соответствующей величины; xi0 − нецелая координата оптимального плана задачи (3.1) − (3.3) с наименьшим индексом; xij − координаты разложения векторов Аj, не попавших в базис; Nk − множество векторов, не попавших в базис. Ниже приводится схема алгоритма метода Гомори (рисунок 3.1).
3.2.2 Метод ветвей и границ У многих задач целочисленного программирования, в частности у сформулированных выше, множество всех допустимых решений представляет собой всевозможные комбинации (перестановки) одного и того же набора чисел. Естественно, что оптимальное решение можно найти, анализируя все возможные варианты. Вопрос лишь в том, как целесообразней организовать такой анализ. Существуют методы динамического программирования, метод ветвей и границ, использующие последовательный анализ вариантов. Рассмотрим второй из них. Пусть G0 − множество допустимых решений задачи, в которой среди совокупности х Возьмем подмножество с меньшей оценкой, допустим G2, и разобьем G2=G3 Подмножество с меньшей оценкой выбираем для ветвления и т.д. (рисунок 3.2).
Рисунок 3.2
Естественно ожидать, что оптимальное решение с большей вероятностью содержится в подмножестве, оценка которого меньше оценок неветвленных подмножеств и, таким образом, производя ветвления, добраться до оптимального решения. 3.2.3 Метод ветвей и границ решения задачи о коммивояжере
Рассмотрим задачу о коммивояжере. Пусть ОПРЕДЕЛЕНИЕ 3.1. Циклом t назовем набор из "n" упорядоченных пар городов, образующих маршрут, который проходит через каждый город только один раз: t = {(i1, i2 ), (i2, i3),…, (in-1, in), (in, i1)}. ОПРЕДЕЛЕНИЕ 3.2. Издержками Z(t) для цикла t назовем величину:
В нашей интерпретации Z(t) − это длина замкнутого маршрута, образованного циклом t. ОПРЕДЕЛЕНИЕ 3.3. Матрица, которая получается из данной вычитанием из элементов каждой строки минимального элемента этой строки, а затемвычитанием из элементов каждого столбца минимального элемента этого столбца, называется приведенной матрицей. Сумма вычитаемых в процессе приведения элементов называется приводящей константой. Если обозначить Si,j(i)=
S'ij=Sij−Si,j(i), i=
Обозначим
минимальный элемент S′ в столбце j. Тогда после вычитания этих элементов получится приведенная матрица S" с неотрицательными элементами
S"ij = S'ij − S'i(j),j,
По определению приводящая константа Если Z(t) − издержки цикла t для исходной матрицы, a Z'(t)−издержки цикла t после приведения, то Z(t)=Z'(t)+h и, очевидно, что h является нижней границей издержек для всех циклов t исходной матрицы расстояний, поскольку h − сумма минимальных элементов строк и столбцов. Из этого следует, что применяя метод ветвей и границ, мы можем использовать h в качестве оценки разветвляемых подмножеств. Определимся теперь с принципом разбиения на подмножества и нахождения оценок этих подмножеств. Пусть G0 − множество всех маршрутов. Разобьем G0 на два подмножества: первое подмножество состоит из всех маршрутов, включающих переезд из города "i" в город "j", говорят содержащих пару (i, j), а второе подмножество состоит из множества маршрутов не содержащих пару (i, j). Пару городов (i, j) для ветвления будем выбирать среди тех пар, которым в приведенной матрице соответствуют нулевые элементы, причем выбирается такая пара (i, j), чтобы подмножество, не содержащее пару (i, j) имело максимальную оценку. Разветвляя последовательно, мы построим дерево ветвей, на вершине которого будет подмножество, содержащее две пары городов, завершающих маршрут. Спускаясь по дереву ветвей, мы по парам городов, определяющих ветвление, определим все пары городов, составляющих маршрут (рисунок 3.3).
Опишем вычислительный алгоритм. 1. Осуществим приведение матрицы S по строкам и столбцам, получим приведенную матрицу S′. 2. Вычислим сумму приводящих констант h(k) - это оценка для исходного множества маршрутов G0. Обозначим оценку ω(G0) = h . 3. Выберем претендентов для ветвления, т.е. те пары (i, j) i=l, 2, ..., j = l, 2, ..., i ≠ j, для которых Sij(k)=0 и вычислим для всех таких Sij(k) величины
4. Выберем для ветвления ту пару (i, j) из претендентов на ветвление, для которой θij получится максимальным. 5. В качестве оценки множества всех маршрутов, не содержащих выбранную пару (i, j), возьмем оценку того множества, которое разветвляли плюс max θij. 6. Так как из каждого города можно выезжать только один раз и в каждый город можно въезжать только один раз, то строку "i" и столбец "j" можно из дальнейшего рассмотрения исключить. Чтобы не получить замкнутых неполных циклов, нужно наложить необходимые запреты, в частности, на переезд из ''j" в "i" то есть положить Sij=∞. 7. Если полученная после вычеркивания строки и столбца и наложения запретов матрица имеет размерность 2x2, то определяемые ею пары городов завершают маршрут. Приводя эту матрицу и добавляя приводящую константу к оценке последнего разветвляемого множества, получим оценку маршрута. Если эта оценка не больше оценки всех тупиковых ветвей, то маршрут, описываемый деревом ветвей, является оптимальным, иначе процесс ветвления должен быть продолжен, исходя из множества с меньшей оценкой. 8. Если усеченная матрица не имеет размерности 2x2, то приводим полученную матрицу и находим оценку множества {i, j}, то есть множества маршрутов, содержащих пару (i, j), как сумму приводящей константы и оценки разветвляемого множества. Переходим к п. 3. Пример 3.1.Имеется четыре пункта, расстояние между которыми описано матрицей расстояний. Найти оптимальный (минимальный) замкнутый маршрут объезда городов.
1 2 13 ∞ 7 8 3 12 7 ∞ 5
1. Приводим матрицу S:
1 2 13 3 12 7 4 4 8 5
2. Найдем сумму приводящих констант: h=4+7+5+4+2=22. Найдем оценку множества G0 : ω(G0 )=22. 3. Укажем претендентов на ветвление и осуществим выбор пары для ветвления:
S14=0, S23= 0, S32=0, S34=0, S41= 0, θ14 =7+0=7, θ23=1+1=2, θ32 = 0 +2=2, θ34=0 +0=0, θ41= 6 + 1=7, max θij=θ14 = 7 ( можно θ41 = 7 ).
4. Итак, для ветвления выбираем пару (1,4) и начинаем строить дерево ветвей (рисунок 3.4). Найдем оценку множества {1,4}−множества всех маршрутов не содержащих пару (1,4): ω({1, 4})=ω(G0)+θ(1,4)=22+7=29. 5. Вычеркнем строку "1", столбец "4" и положим запрет на переезд из "4" в"1":
2 6 3 7 0 4
Приводим матрицу
2 6 3 7 0 4
6. Найдем h = 1 + 6 = 7 и оценку {1, 4 }.
ω({1, 4})=ω(G0)+h=22+7=29.
7. Укажем претендентов для ветвления и выберем пару для ветвления:
S21 = 0, S23 = 0, S32 = 0, S43 = 0,
θ21 = 0 + 1 = 1, θ23 = 0 + 0 = 0 , θ32 = 1+ 1 = 2, θ43=1+0 = 1, max θij = θ32 = 2.
Итак, для ветвления берем пару (3,2). Найдем оценку 8. Вычеркнем строку "3", столбец "2" и наложим запрет на переезд из "2" в "3".
1 3
4
ω({3, 2})=ω({1, 4})+h=29.
9. Так как матрица размерности 2x2, то не запрещенные пары (2,1) и (4,3) завершают маршрут (рисунок 3.4).
Рисунок 3.4 − Маршрут объезда пунктов
Поскольку оценка последнего подмножества не больше оценок тупиковых ветвей, то пары (1,4), (3,2), (2,1), (4,3) задают оптимальный маршрут, который можно представить, скажем так: 1→4 →3 →2 →1 с расстоянием Smin=29.
3.2.4 Аппроксимация решения задачи о коммивояжере
Приведенный в предыдущем пункте алгоритм является чрезвычайно трудоемким даже при использовании ЭВМ. В практически приемлемое время он позволяет решать лишь задачи небольшой размерности. В [5] предложено производить декомпозицию задачи большой размерности на ряд задач приемлемой размерности разбиением на группы (зоны) "близких" друг к другу объектов. В каждой группе выбираются объекты (вообще говоря разные), которые служат представителями группы (зоны) при определении минимальных расстояний между группами (зонами). Используя описанный выше алгоритм находят, на первом этапе, оптимальный межгрупповой (межзональный) маршрут, а на втором этапе в каждой группе (зоне) ищут кратчайший маршрут между теми объектами группы (зоны), которые служат их представителями в межзональных расстояниях. Для того, чтобы построить минимальный незамкнутый маршрут между двумя представителями группы, с обязательным посещением всех остальных объектов группы, расстояния между этими двумя представителями переопределяют достаточно большими числами (накладывают "запрет" на ранний переезд) и затем этот переезд из оптимального внутригруппового маршрута выбрасывают. Полученный таким образом маршрут достаточно хорошо аппроксимирует искомый оптимальный маршрут при удачном разбиении на группы.
|
||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 403. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
.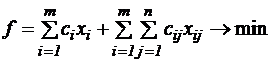
 0, xij
0, xij  (производимая продукция полностью потребляется);
(производимая продукция полностью потребляется); (каждый потребитель получает продукции в объеме, не менее заданного значения);
(каждый потребитель получает продукции в объеме, не менее заданного значения);

 = 1, j=1,2,…,n (На каждое предприятие по одному виду оборудования),
= 1, j=1,2,…,n (На каждое предприятие по одному виду оборудования), = 1, i = 1,2,…,n (Каждая единица оборудования распределяется на 1 предприятие).
= 1, i = 1,2,…,n (Каждая единица оборудования распределяется на 1 предприятие).

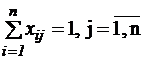

 n – 1,
n – 1,  ,
,  , i≠j,
, i≠j, (3.1)
(3.1)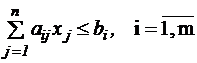 (3.2)
(3.2) допустимые целые, то полученное оптимальное решение задачи линейного программирования является оптимальным решением задачи целочисленного программирования;
допустимые целые, то полученное оптимальное решение задачи линейного программирования является оптимальным решением задачи целочисленного программирования; ,
,

 G0 требуется найти то х, при котором целевая функция f имеет минимум. По некоторому закону (правилу) поставим в соответствие множеству G0 число Z0, которое является оценкой нижней границы целевой функции на множестве G0. Разобьем множество G0 на конечное число непересекающихся подмножеств (для наглядности на два) G1 и G2: G0=G1
G0 требуется найти то х, при котором целевая функция f имеет минимум. По некоторому закону (правилу) поставим в соответствие множеству G0 число Z0, которое является оценкой нижней границы целевой функции на множестве G0. Разобьем множество G0 на конечное число непересекающихся подмножеств (для наглядности на два) G1 и G2: G0=G1  G2, G1
G2, G1  G2=Ø. Определим по выбранному закону (правилу) оценки нижней границы целевой функции на этих подмножествах Z1 и Z2.
G2=Ø. Определим по выбранному закону (правилу) оценки нижней границы целевой функции на этих подмножествах Z1 и Z2.

 матрица, элемент которой Sij определяет расстояние при переходе из пункта «i» в пункт «j». Полагаем Sii=
матрица, элемент которой Sij определяет расстояние при переходе из пункта «i» в пункт «j». Полагаем Sii=  , i=
, i=  , рассматриваем это как запрет на переезд из "i" в "i".
, рассматриваем это как запрет на переезд из "i" в "i". .
. Si,j, i=
Si,j, i=  −минимальный элемент S в строке "i", тогда после вычитания этих элементов получится матрица S' с неотрицательными элементами
−минимальный элемент S в строке "i", тогда после вычитания этих элементов получится матрица S' с неотрицательными элементами .
.
 .
. 

 1234
1234


 1234 123 4
1234 123 4  0 2 0 0
0 2 0 0 
 1 2 3
1 2 3 



 123
123 
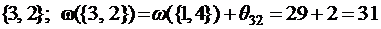 .
.
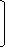 2 0
2 0