
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Причинно-следственные связи между явлениями. Качественный анализ изучаемого явления.Исследование объективно существующих связей между явлениями – важнейшая задача общей теории статистики. В процессе статистического исследования вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие существенное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, при которой изменение одного из них – причины – ведет к изменению другого – следствия. Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении этих явлений необходимо, абстрагируясь от второстепенных, выявлять главные, основные причины. В основе первого этапа статистического изучения связей лежит качественный анализ явления, связанный с анализом его природы методами экономической теории, социологии, конкретной экономики. Второй этапа – построение модели связи. Она базируется на методах статистики: группировки, средних величин, таблиц и т.д. Третий последний этап – интерпретация результатов, вновь связан с особенностями изучаемого явления. Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и поставленных задач. Связи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований. Признаки, обуславливающие изменение других, связанных с ними признаков, называются факторными, или просто факторами. Признаки, изменяющиеся под действием факторных признаков, являются результативными. Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению.  В статистике различают функциональную связь и стохастическую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Функциональная связь проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности. Если причинная зависимость проявляется не в каждом отдельном случае, а в общем среднем, при большом числе наблюдений, то такая зависимость называется стохастической. Частным случаем стохастической является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков. По степени тесноты связи различают количественные критерии (таблица 1). Таблица 1 Количественные критерии оценки тесноты связи
По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного. В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной, экспоненциальной и т.д.), то такую связь называют нелинейной, или криволинейной. В статистике не всегда требуются количественные оценки связи, часто важно определить лишь ее направление и характер, выявить форму воздействия одних факторов на другие. Для выявления наличия связи, ее характера и направления в статистике используются методы приведения параллельных данных; аналитических группировок; графический; корреляционный, регрессионный. Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. Статистическую связь между двумя признаками можно изобразить графически и по графику судить о наличии, направлении и форме связи. На оси абсцисс откладываются значения факторного признака, на оси ординат – результативного. На графике откладываются все единицы, обладающие определенными значениями х и у. При отсутствии тесных связей наблюдается беспорядочное расположение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи. Корреляционный метод имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи). Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. Первоначально исследования корреляции проводились в биологии, а позднее распространились и на другие области, в том числе на социально-экономическую. Одновременно с корреляцией начала использоваться и регрессия. Корреляция и регрессия тесно связаны между собой: корреляция оценивает силу (тесноту) статистической связи, регрессия исследует ее форму. Та и другая служат для установления соотношения между явлениями, для определения наличия или отсутствия связи. Корреляционный и регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ). Функциональной называют связь, при которой каждому конкретному значению факторного признака соответствует одно или несколько определенных значений результативного признака. Функциональная связь двух величин возможна лишь при условии, что вторая из них на 100% зависит только от первой и ни от чего более. Функциональная связь чаще встречается в точных науках, например, площадь квадрата характеризуется следующей функциональной связью: Пример функциональной связи в экономике: при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий x при фиксированной расценке за одну деталь, например 5 руб., можно выразить формулой: Стохастической (вероятностной) называют связь, при которой каждому значению факторного признака соответствует определенное распределение вероятностей появление того или иного значения результативного признака. Статистической называют связь, при которой каждому значению факторного признака соответствует определенное статистическое (выборочное) распределение результативного признака. Статистическая связь является частным случаем стохастической, она устанавливается на основе выборочных данных. Корреляционной называют связь, при которой каждому значению факторного признака соответствует условное среднее значение результативного признака. Корреляционная связь является частным случаем статистической связи. В статистике различают следующие виды корреляционной связи: а) парная корреляция – связь между результативным и одним факторным признаками; б) частная корреляция – связь между результативным и одним факторным признаками, при фиксированных значения других факторных признаков; в) множественная корреляция – связь между результативным и двумя или более факторными признаками. Взаимосвязь явлений удобно представлять в табличной и графической формах. Таблицу, в которой значениям результативного признака соответствуют значения факторных признаков называют корреляционной таблицей (от лат. correlatio – соотношение, взаимосвязь) Корреляционным полем называют график, представляющий совокупность точек с координатами ( Кроме того, выделяют прямую и обратную, а также линейную и нелинейную причинно-следственную связь. Прямой называют связь, при которой с увеличением значений факторных признаков, значения результативного также возрастают и наоборот. Обратной называют связь, при которой с увеличением значений факторных признаков, значения результативного – убывают, и наоборот. Линейной называют связь, при которой одинаковым приращениям факторных признаков соответствуют одинаковые приращения результативного. Линейная связь характеризуется следующей аналитической зависимостью: Нелинейной называют связь, при которой одинаковым приращениям факторных признаков соответствуют неодинаковые приращения результативного. Например, нелинейная связь может характеризоваться параболической зависимостью ( Укрупненно схему статистического исследования взаимосвязи между изучаемыми явлениями можно представить последовательностью следующих этапов: 1. Качественный анализ изучаемого социально-экономического явления, связанный с анализом его природы методами экономической теории, социологии и др.; 2. Построение модели корреляционной связи, используя статистический инструментарий: 2.1. Выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками и измерение тесноты связи между двумя (и более) признаками. Данную часть исследования называют корреляционным анализом. 2.2. Определение уравнения регрессии – математической модели, в которой среднее значение результативного признака рассматривается как функция одной или нескольких переменных – факторных признаков. Данная часть исследования называется регрессионным анализом. Задача 1.По условным данным таблицы 10 о стоимости основных фондов х и валовом выпуске продукции у (в порядке возрастания стоимости основных фондов) выявить наличие и характер корреляционной связи между признаками x и y. Таблица 10. Стоимость основных фондов и валовой выпуск по 10 однотипным предприятиям
Решение. Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется рядметодов.
зависимости между признаками x и y. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции. 2. Рассмотрение параллельных данных (значений x и y в каждой из n единиц). Единицы наблюдения располагают по возрастанию значений факторного признака х и затем сравнивают с ним (визуально) поведение результативного признака у. В нашей задаче в большинстве случаев по мере увеличения значений x увеличиваются и значения y (за несколькими исключениями – 2 и 3, 6 и 7 предприятия), поэтому, можно говорить о прямой связи между х и у (этот вывод подтверждает и эмпирическая линия регрессии). Теперь необходимо ее измерить, для чего рассчитывают несколько коэффициентов. 3. Коэффициент корреляции знаков (Фехнера) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x и y) от своей средней величины. При этом во внимание принимаются не величины отклонений (
Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ=1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ=–1(обратная связь). Если жеåС=åН, то КФ=0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до В нашей задаче В двух последних столбцах таблицы 10 приведены знаки отклонений каждого х и у от своей средней величины. Число совпадений знаков – 9, а несовпадений – 1. Отсюда КФ= 4.Линейный коэффициент корреляции применяется в случае линейной зависимости между двумя количественными признаками x и y. В отличие от КФ в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:
Линейный коэффициент корреляции r представляет собой среднюю величину из произведений нормированных отклонений для x и у:
Числитель формулы (84), деленный на n, т.е.
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если В нашей задаче для расчета rпостроим вспомогательную таблицу 11. Таблица 11. Вспомогательные расчеты линейного коэффициента корреляции
В нашей задаче: Проверка коэффициента корреляции на значимость (существенность). Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан. Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того, чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между х и у, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σr. Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой: Существуют некоторые особенности расчета σr в зависимости от числа наблюдений (объема выборки) – n. 1. Если число наблюдений достаточно велико (n>30), то σr рассчитывается по формуле (86):
Обычно, если доверительные пределы (границы)r = ( 2. Если число наблюдений небольшое (n<30), то σr рассчитывается по формуле (87):
а значимость r проверяется на основе t-критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (88) и сопоставляется ctТАБЛ.
Табличное значение tТАБЛ находится по таблице распределения t-критерия Стьюдента (см. приложение 2) при уровне значимости α=1-β и числе степеней свободы ν=n–2. Если tРАСЧ>tТАБЛ,то r считается значимым, а связь между х и у – реальной. В противном случае (tРАСЧ<tТАБЛ) считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно. В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам (87) и (88): 5. Подбор уравнения регрессии представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие нау и не связанные с х, не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака усо значениями факторного признака х. Уравнение регрессии можно также назвать теоретической линией регрессии. Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими.Они обычно обозначаются Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х и у, — одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей. Для аналитической связи между х и умогут использоваться следующие простые виды уравнений:
Обычно зависимость, выражаемую уравнением прямой, называют линейной (или прямолинейной), а все остальные — криволинейными зависимостями. Выбрав тип функции, по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов (МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака
Поставив данное условие, легко определить, при каких значениях
Исходные данные и все расчеты необходимых сумм представим в таблице 12. Таблица 12. Вспомогательные расчеты для решения задачи
Отсюда искомая линия регрессии:
Рис.6. График эмпирической и теоретической линий регрессии. 6. Теоретическое корреляционное отношение представляет собой универсальный показатель тесноты связи. Измерить тесноту связи между коррелируемыми величинами – это значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака. Ранее были рассмотрены показатели, с помощью которых можно выявить наличие корреляционной связи между двумя признаками x и y и измерить тесноту этой связи: коэффициент Фехнера и линейный коэффициент корреляции. Наряду с ними существует универсальный показатель – корреляционное отношение (или коэффициент корреляции по Пирсону), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционные отношения. Эмпирическое корреляционное отношение рассчитывается на основе правила сложения дисперсий как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии, т.е.
Теоретическое корреляционное отношение
Сравнивая вторую дисперсию с первой, получим теоретический коэффициент детерминации:
который показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение:
Оно может находиться в пределах от 0 до 1. Чем ближе его значение к 1, тем теснее связь между вариацией y и x. При зависимости между коррелируемыми величинами, при 0,3< В нашей задаче расчет необходимых сумм для использования в формуле (93) приведен в последних двух столбцах таблицы 12. Тогда теоретический коэффициент детерминации по формуле (93) равен: Теоретическое корреляционное отношение по формуле (94) равно:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 1121. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . При увеличении, к примеру, стороны квадрата в два раза, его площадь увеличиться в 4 раза. Другой пример функциональной связи:
. При увеличении, к примеру, стороны квадрата в два раза, его площадь увеличиться в 4 раза. Другой пример функциональной связи:  (в данном случае, к примеру, значению
(в данном случае, к примеру, значению  соответствует два значения:
соответствует два значения:  и
и  ).
). .
. ,
,  ). Эмпирической линией регрессии(от лат. regressio – движение назад) называют ломанную, вершины которой имеют координаты (
). Эмпирической линией регрессии(от лат. regressio – движение назад) называют ломанную, вершины которой имеют координаты (  ).
). .
. ), гиперболической (
), гиперболической (  ) и др.
) и др.

 1. Графический метод, когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии (см. рисунок справа). Анализируя эту линию, визуально можно определить характер
1. Графический метод, когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n взаимосвязанных пар значений x и y и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x и y. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии (см. рисунок справа). Анализируя эту линию, визуально можно определить характер .(82)
.(82) 1. Однако, если КФ=1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.
1. Однако, если КФ=1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х и у.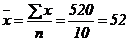 ;
;  .
. =0,8. Обычно такое значение показателя тесноты связи характеризует сильную зависимость, однако, следует иметь в виду, что поскольку КФ зависит только от знаков и не учитывает величину самих отклонений х и уот их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
=0,8. Обычно такое значение показателя тесноты связи характеризует сильную зависимость, однако, следует иметь в виду, что поскольку КФ зависит только от знаков и не учитывает величину самих отклонений х и уот их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление. и
и  .
. , (83) или
, (83) или  . (84)
. (84) , представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и уна произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например:
, представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и уна произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например: .(85)
.(85) , то r по формуле (85) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r<0) – обратную связь. Если
, то r по формуле (85) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r<0) – обратную связь. Если  , то r=0, что означает отсутствие линейной зависимости между х и у, а при r=1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи междух и у к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная.
, то r=0, что означает отсутствие линейной зависимости между х и у, а при r=1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи междух и у к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная.



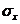 =
=  =29,299;
=29,299;  =
=  =65,436. Тогда по формуле (83)r = 9,516166/10 = 0,9516. Аналогичный результат получаем по формуле (84): r = 1824,4/(29,299*65,436) = 0,9516 или по формуле (85): r = (7024,4 – 52*100) / (29,299*65,436) = 0,9516, то есть связь между величиной основных фондов и валовым выпуском продукции очень близка к функциональной.
=65,436. Тогда по формуле (83)r = 9,516166/10 = 0,9516. Аналогичный результат получаем по формуле (84): r = 1824,4/(29,299*65,436) = 0,9516 или по формуле (85): r = (7024,4 – 52*100) / (29,299*65,436) = 0,9516, то есть связь между величиной основных фондов и валовым выпуском продукции очень близка к функциональной. .
. .(86)
.(86)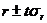 ), где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. таблицу 4).
), где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. таблицу 4). ,(87)
,(87) .(88)
.(88)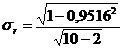 = 0,3073/2,8284 = 0,1086;
= 0,3073/2,8284 = 0,1086;  = 0,9516/0,1086 = 8,7591. При вероятности 95% tтабл=2,306, а при вероятности 99% tтабл=3,355, значит, tРАСЧ>tТАБЛ, что дает возможность считать линейный коэффициент корреляции r= 0,9516 значимым.
= 0,9516/0,1086 = 8,7591. При вероятности 95% tтабл=2,306, а при вероятности 99% tтабл=3,355, значит, tРАСЧ>tТАБЛ, что дает возможность считать линейный коэффициент корреляции r= 0,9516 значимым.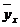 (читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.
(читается: «игрек, выравненный по х») и рассматриваются как функция от х, т.е.  .)
.)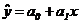 – прямая линия;
– прямая линия;  – парабола;
– парабола; – гипербола;
– гипербола; 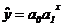 – показательная функция;
– показательная функция; – логарифмическая функция и др.
– логарифмическая функция и др. .
.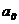 ,
,  и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в методических указаниях к теме 4 «Ряды динамики», поэтому, воспользуемся формулой (57)для нахождения параметров теоретической линии регрессии в нашей задаче, заменив параметр t на x.
и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в методических указаниях к теме 4 «Ряды динамики», поэтому, воспользуемся формулой (57)для нахождения параметров теоретической линии регрессии в нашей задаче, заменив параметр t на x. (89)
(89)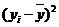

 ;
; 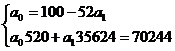 ;
;  ;
; ;
;  ;
;  ;
;  =–10,5+2,125x. Для иллюстрации построим график эмпирической (маркеры-кружочки) и теоретической (маркеры-квадратики) линий регрессии.
=–10,5+2,125x. Для иллюстрации построим график эмпирической (маркеры-кружочки) и теоретической (маркеры-квадратики) линий регрессии.
 .(90)
.(90) определяется на основе выравненных (теоретических) значений результативного признака
определяется на основе выравненных (теоретических) значений результативного признака  , рассчитанных по уравнению регрессии.
, рассчитанных по уравнению регрессии.  , а теоретического ряда –
, а теоретического ряда –  , то каждая из них выразится формулами:
, то каждая из них выразится формулами: ,(91)
,(91) .(92)
.(92) ,(93)
,(93)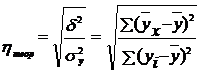 .(94)
.(94) <0,3 говорят о малой
<0,3 говорят о малой .
. = 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами.
= 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами.