
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Практические занятия 5, 6, 7. Применение метода наименьших квадратов в случае показательной, логарифмической и гиперболической зависимостей.Пример 1. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости
Нанесем табличные данные на график. Расположение точек позволяет сделать вывод: функция при малых значениях переменной (x < 5) меняется слабо, а при больших значениях – резко возрастает, что свидетельствует в пользу выбора экспоненциальной зависимости Проведем необходимые вычисления.
Заполним таблицу значениями функции.
Нанесем полученные точки на график и соединим плавной линией, которая весьма удовлетворительно соответствует исходным данным. Пример 2. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости Отметим табличные значения на координатной плоскости (нанесение точек выполнить самостоятельно). Плавное изменение значений функции свидетельствует в пользу выбора логарифмической зависимости Числовые параметры выбранной зависимости найдём по формулам (5) и (6), представленным в лекции 3. Чтобы воспользоваться формулами, вычислим необходимые для этого суммы. 
Вычислим отдельно знаменатель в формулах (7) и (8), обозначив его Δ.
Формула искомой зависимости будет иметь вид: Для проверки результата составим таблицу значений (округлённых так же, как и обрабатываемые данные, до сотых) найденной аналитической зависимости и нарисуем её график вместе с исходными данными.
Построенный график очень хорошо соответствует экспериментальным данным, значит, выбор аналитической зависимости можно считать верным. Пример 3. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости
Нанесем табличные данные на график. Сильное изменение функции при небольших Параметры выбранной зависимости найдём по формулам (7) и (8), представленным в лекции 3. Выполним необходимые вычисления:
Составим таблицу значений функции, округлив их до десятых, как и в исходной таблице.
Нанесем рассчитанные значения на график и соединим плавной линией. Точки, соответствующие исходным данным хорошо группируются вблизи проведенной линии, значит, зависимость выбрана удовлетворительно. Задание 1 для самостоятельной работы. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости Задание 2 для самостоятельной работы. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости Задание 3 для самостоятельной работы. Результаты экспериментального исследования величины y от величины x представлены в таблице.
Методом наименьших квадратов найти формулу функциональной зависимости |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 289. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 .
.
 . Для определения её числовых параметров используем формулы (3) и (4) из лекции 3.
. Для определения её числовых параметров используем формулы (3) и (4) из лекции 3.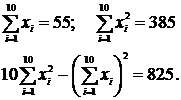
 ;
;


 .
. ;
; ;
; ;
;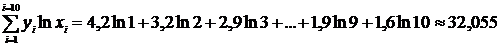 ;
;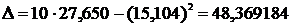 .
.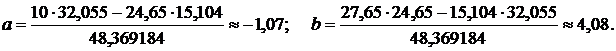
 .
.

 и очень незначительное при больших
и очень незначительное при больших  указывает на возможность выбрать для данного случая гиперболическую зависимость
указывает на возможность выбрать для данного случая гиперболическую зависимость  .
. ;
; ;
; ;
; ;
; ;
; ;
; 
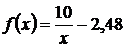 .
.