
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание 2. Фильтрация сигналов для демодуляции амплитудно-манипулированных сигналов в гауссовских каналах связи.Задание 1. Демодуляция АМ-сигнала Порядок выполнения работы: 1) Зададим временной массив t: 0≤t≤1; 2) Зададим линейные частоты модулирующего 3) Зададим амплитуду несущегосигнала 4) Зададим коэффициент модуляции m: 0<m≤1 (при m>1 наступает перемодуляция(избыточная модуляция)), простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями. 5) Сгенерируем несущий сигнал и модулирующий сигнал, используя входные параметры:
6) Сгенерируем амплитудно-модулированный сигнал
Т.к.
7) Сгенерируем массив случайных величин (соразмерный смассивом t),распределенных по равномерному закону в интервале (0, 1)[белый шум
8) Проведем фильтрацию принимаемого сигнала Операция линейной дискретной фильтрации в общем случае описывается следующим образом:
Максимальное из чисел
Рис 1. Цифровой рекурсивный фильтр Передаточная функция фильтра имеет вид:
В среде MatLab используется функция 9) Зададим параметры фильтра:
И проведем операцию демодуляции принимаемого сигнала.
10) Вычислим отношение сигнал/шум по формуле:
Листинг программы clear t=0:0.001:1; %Задаем массив отсчетов времени fc=100; %Задаем частоту несущего сигнала  fm=10; %Задаем частоту модулирующего сигнала Uc0=3; %Задаем амплитуду несущего колебания Um0=2; %Задаем амплитуду модулирующего сигнала U0=3; %Задаем постоянную составляющую модулирующего сигнала Un0=0.1; %Задаем амплитуду белого шума fi0=pi/3; %Задаем начальную фазу модулирующего колебания m=1; %Задаем коэффициент модуляции Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание Um=U0+Um0*cos(2*pi*fm*t+fi0); %Задаем модулирующий гармонический сигнал Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); %Выражение для АМ-сигнала Un=Un0*randn(size(t)); %Генерирует белый шум с МО=0 и СКО=1 Ud=Uam+Un; %Сигнал на входе приемника (аддитивная помеха) b=[1 1 1]; %Коэффиенты b цифрового фильтра a=1; %Коэффициенты a цифрового фильтра Udmd=filter(b,a,abs(Ud)); subplot(3,2,1) plot(t,Um) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Модулирующийсигнал') subplot(3,2,2) plot(t,Uc) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Несущееколебание') subplot(3,2,3) plot(t,Uam) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('АМсигнал') subplot(3,2,4) plot(t,Un) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Белыйшум') subplot(3,2,5) plot(t,Ud) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Сигнал на входе приемника') subplot(3,2,6) plot(t,Udmd) grid on xlabel('Время, с') ylabel('Амплитуда, B') title ('Отфильтрованный сигнал')
Задание 2. Фильтрация сигналов для демодуляции амплитудно-манипулированных сигналов в гауссовских каналах связи.
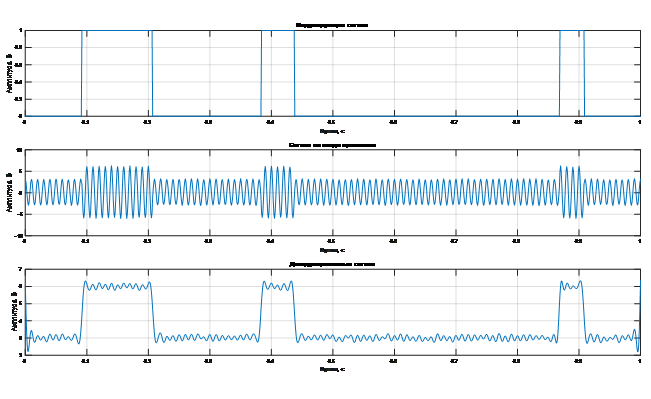
Проделаем задание 2 аналогично заданию 1 с той лишь разницей, что в качестве модулирующего сигнала будет выступать битовая последовательность. В задании использовался модифицированный код из предыдущего задания.
Рис 2. Временное представление модулирующей битовой последовательности, детектируемого сигнала и демодулированного сигналов
Задание 3. Обнаружение детерминированного импульсного сигнала Порядок выполнения работы: 1) Введём известные данные и посчитаем порог Байса для принятия решения
2) Из теории проверки статистических гипотез имеем:
Необходимо проверить соотношение:
Так как помеха, сгенерированная в задании 2, имеет математическое ожидание МО=0 и среднеквадратическое отклонение СКО=1, то:
Листинг программы t=0:0.001:1; %Задаем массив отсчетов времени fc=100; %Задаем частоту несущего сигнала fm=10; %Задаем частоту модулирующего сигнала Uc0=3; %Задаем амплитуду несущего колебания Um0=2; %Задаем амплитуду модулирующего сигнала U0=3; %Задаем постоянную составляющую модулирующего сигнала fi0=pi/3; %Задаем начальную фазу модулирующего колебания m=1; %Задаем коэффициент модуляции Un0=0.3; %Задаем амплитуду белого шума Uc=Uc0*cos(2*pi*fc*t); %Задаем несущее гармоническое колебание Um=U0+Um0*cos(2*pi*fm*t+fi0); %Задаем модулирующий гармонический сигнал Uam=Uc0.*(1+m*Um/max(abs(Um))).*cos(2*pi*fc*t); %Выражение для АМ-сигнала Un=Un0*randn(size(t)); %Генерирует белый шум с МО=0 и СКО=1 Ud=Uam+Un; %Сигнал на входе приемника (аддитивная помеха) U1=Un.^2; U2=Um.^2; U3=U1+U2; U4=U3'; L=2.71828^(sum(U4)); disp('Отношение правдоподобий') disp(L)
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 270. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
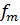 и несущего
и несущего  колебаний.
колебаний. . Для модулирующего сигнала зададим амплитуду
. Для модулирующего сигнала зададим амплитуду  , постоянную составляющую
, постоянную составляющую  , и начальную фазу колебаний
, и начальную фазу колебаний  .
.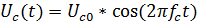 ;
; ;
; :
: ;
; ;
; ]. Зададим его амплитуду
]. Зададим его амплитуду 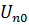 . В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид:
. В канале связи будет создаваться аддитивная помеха, т.е. сигнал на входе приемника будет иметь вид: ;
; ;
;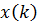 — отчёты входного сигнала;
— отчёты входного сигнала; — отчёты выходного сигнала;
— отчёты выходного сигнала; —постоянные коэффициенты;
—постоянные коэффициенты; и
и  называется порядком фильтра.
называется порядком фильтра.
 ;
; .
. ;
; ;
; ;
;
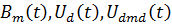
 ;
; на фоне АБГШ.
на фоне АБГШ. :
: ;
; ;
; ;
; ;
; ;
; – гипотеза о том, что в сигнале
– гипотеза о том, что в сигнале  присутствует
присутствует  ;
; – гипотеза о том,в сигнале
– гипотеза о том,в сигнале 



 , следовательно, на основании критерия Байса принимается гипотеза
, следовательно, на основании критерия Байса принимается гипотеза