
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчет коэффициентов теплопередачиРассчитываем коэффициент теплоотдачи от конденсирующегося пара к стенке трубы
Здесь Тогда удельная тепловая нагрузка равна
Выбераем в качестве конструкционного материала аппарата сталь Х18Н10Т, стойкую в среде кипящего раствора NaClв интервале изменения концентраций от 5 до 25%. Коэффициент теплопроводности стал Суммарное термическое сопротивление стенки
Перепад температур на стенке При
Получаем удельную тепловую нагрузку
Перепад температур на стенке Тогда Для расчета коэффициента теплоотдачи от стенки к кипящему раствору используем критериальное уравнение(20)
Значения физических параметров, входящих в критерии, находим с помощью таблиц приложения при температуре в кипятильных трубах. Рассчитываем критерий Рейнольдса
и затем критерий Нуссельта
Тогда коэффициент теплоотдачи со стороны раствора равен
Значение удельной тепловой нагрузки
что также говорит о неверном выборе Из полученных результатов можно сделать вывод, что истинное значение Задаваясь последовательно несколькими значениями
Тогда коэффициент теплопередачи в первом корпусе равен
Выполняя аналогичные расчеты для второго и третьего корпусов в последних расчетах получим:  для второго корпуса:
для третьего корпуса:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 305. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
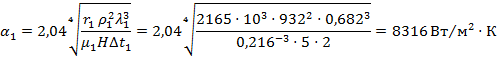
 принята в первом приближении. Неизвестные параметры найдены по таблицам приложения.
принята в первом приближении. Неизвестные параметры найдены по таблицам приложения.


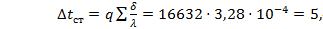
 такой результат нереален. Поэтому задаемся новым значением
такой результат нереален. Поэтому задаемся новым значением 




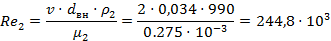


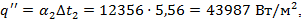

 находится в интервале от 1 до 2 град.
находится в интервале от 1 до 2 град. В этом случае получим:
В этом случае получим: ,
, 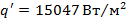 ,
,  ,
, ,
, 
 ассчитываем среднее значениеудельной тепловой нагрузки:
ассчитываем среднее значениеудельной тепловой нагрузки:

 ,
,  ,
,  ,
, 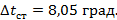 ,
, ,
, 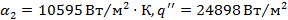 ,
, 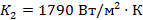
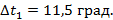 ,
,  ,
,  ,
,  ,
, ,
,  ,
, 