
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчеты с использованием уравнения МайераВ практических расчётах часто используют удельную массовую теплоемкость, и как раз она обычно приводится в таблицах теплофизических величин. Умножив молярную теплоёмкость газа на его молярную массу, мы получим удельную массовую теплоемкость: Уравне́ниеПуассо́на — эллиптическоедифференциальное уравнение в частных производных, которое описывает · электростатическое поле, · стационарное поле температуры, · поле давления, · поле потенциала скорости в гидродинамике. Оно названо в честь знаменитого французскогофизика и математикаСимеона Дени Пуассона. Это уравнение имеет вид:Δ φ = f , {\displaystyle \Delta \varphi =f,} где Δ {\displaystyle \Delta } — оператор Лапласа, или лапласиан, а f {\displaystyle f} — вещественная или комплекснаяфункция на некотором многообразии. В трёхмерной декартовой системе координат уравнение принимает форму:( ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 ) φ ( x , y , z ) = f ( x , y , z ) . {\displaystyle \left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)\varphi (x,y,z)=f(x,y,z).} В декартовой системе координат оператор Лапласа записывается в форме∇ 2 {\displaystyle \nabla ^{2}} и уравнение Пуассона принимает вид:∇ 2 φ = f . {\displaystyle {\nabla }^{2}\varphi =f.} Если f {\displaystyle f} стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона): Δ φ = 0. {\displaystyle \Delta \varphi =0.} Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».  4. При рассмотрении закона распределения Максвелла предполагалось, что молекулы равномерно распределяются по всему объему сосуда, что справедливо, если объем сосуда небольшой. Для больших объемов равномерность распределения молекул по объему нарушается из-за действия силы тяжести, вследствие чего плотность, а следовательно, и число молекул в единице объема будут неодинаковым. Рассмотрим молекулы газа, находящегося в поле тяготения Земли. Выясним зависимость давления атмосферы от высоты над поверхностью Земли. Допустим, на поверхности Земли (h = 0) давление атмосферы P0. На высоте h оно равно P. При увеличении высоты на dh давление уменьшится на dP: dP = - ρgdh (9.49) [ρ — плотность воздуха на данной высоте, ρ = mn0, где m — масса молекулы, n0 — концентрация молекул]. Используя соотношение P = n0kТ, получаем тогда
Полагая, что на некоторой высоте h Т = соnst, g = соnst, разделяя переменные, интегрируем выражение (9.50):
Получаем
Барометрическая формула показывает зависимость давления газа от высоты над поверхностью Земли. Если учесть, что концентрация молекул воздуха в атмосфере определяет давление, то формулу (9.51) можно записать в виде
Из формулы (9.52) следует, что с понижением температуры число частиц на высоте, отличной от нуля, убывает и при Т = 0К обращается в нуль, т. е. при 0К все молекулы расположились бы на земной поверхности. Так как потенциальная энергия молекул на различной высоте различна и на высоте h определяется по формуле где ЕП = mgh, то [см.
— закон Больцмана, показывающий распределение участвующих в тепловом движении молекул в потенциальном поле сил, в частности в поле силы тяжести. 5. Важной характеристикой термодинамической системы является ее внутренняя энергияU — энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Из этого определения следует, что к внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. Внутренняя энергия — однозначная функция термодинамического состояния системы, т. е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Это означает, что при переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода. В § 1 было введено понятие числа степеней свободы — числа независимых переменных (координат), полностью определяющих положение системы в пространстве. В ряде задач молекулу одноатомного газа (рис. 77, а) рассматривают как материальную точку, которой приписывают три
89 степени свободы поступательного движения. При этом энергию вращательного движения можно не учитывать (r—>0, J= mr2®0, Tвр =Jw2/2®0). В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 77,б). Эта система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степенями свободы (i=5). Трехатомная (рис. 77,0) и многоатомная нелинейные молекулы имеют шесть степеней свободы: три поступательных и три вращательных. Естественно, что жесткой связи между атомами не существует. Поэтому для реальных молекул необходимо учитывать также степени свободы колебательного движения. Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <e0)в (43.8): 6.Напомним, что под числом степеней свободы тела понимают наименьшее число независимых координат, необходимых для полного определения положения тела. Л. Больцман установил закон равномерного распределения энергии молекул идеального газа по степеням свободы:на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kT/2. Таким образом, молекула с i-степенями свободы обладает средней кинетической энергией, равной
Рис.20.1
Заметим, что при определении числа степеней свободы молекул газов принимаются во внимание те степени свободы, которые вносят существенный вклад в ее кинетическую энергию. Например, молекула одноатомного газа, принимаемая за материальную точку (рис.20.1.а) и способная совершать три независимых движениях (вдоль осей X, Y и Z), имеет три степени свободы. Следовательно, средняя кинетическая энергия такой молекулы Молекулу двухатомного газа можно представить в виде двух атомов, жестко связанных друг с другом (рис.20.1.б). Кроме трех степеней свободы поступательного движения, такая система имеет еще две степени свободы вращения вокруг осей Y и Z (вращение вокруг третьей оси X не вносит вклада в энергию молекулы, так как момент инерции молекулы относительно этой оси ничтожно мал). Таким образом, двухатомная молекула имеет пять степеней свободы и, следовательно, обладает средней кинетической энергией Молекулы, состоящие из трех и более атомов, имеют шесть степеней свободы: три поступательных и три вращательных (рис.20.1.в). Для таких молекул Строго говоря, связи между атомами в молекулах реальных газов не являются абсолютно жесткими, поэтому при некоторых условиях (например, при повышенных температурах) эти связи скорее можно представить в виде упругих пружин, результатом чего являются дополнительные, колебательные степени свободы. Закон равномерного распределения энергии по степеням свободы приводит к выводу о равноправности всех степеней свободы молекулы: все они вносят одинаковый вклад в ее среднюю кинетическую энергию.Однако этот вывод имеет ограниченную область применимости и уточнен в квантовой статистике. 7. Исходным постулатом первого начала термодинамики является закон сохранения энергии: Энергия изолированной системы сохраняет постоянную величину при всех изменениях, происходящих в этой системе, или, что то же, энергия не возникает из ничего и не может обратиться в ничто. Важнейшим моментом в построении первого начала термодинамики является введение понятия внутренней энергии термодинамической системы (В. Томсон, 1851 г.). С точки зрения кинетической теории строения вещества внутренняя энергия термодинамической системы измеряется уровнем кинетической энергии и энергии взаимодействия материальных частиц этой системы, однако подобные воззрения недостаточны для объяснения всех известных явлений выделения энергии (химические , внутриатомные, внутриядерные процессы, электомагнитные, гравитационные и другие взаимодействия.) Вопрос об истинной природе внутренней энергии тел тесно связан с изучением строения материи, причём решение этой специальной задачи, базирующееся на представлениях о природе непосредственно ненаблюдаемых явлений, выходит за рамки возможностей лишь одного закона сохранения энергии. Поэтому в основу построений основных принципов термодинамики может быть положено лишь такое общее определение внутренней энергии тел, которое не ограничивает возможностей строгого построения термодинамики на базе постулатов общечеловеческого опыта. Внутренней энергией термодинамической системы называется полный запас энергии её внутреннего состояния, определяемый в зависимости от деформационных координат и температуры: u = u ( x 1 , x 2 , . . . x n , t ) {\displaystyle u=u(x_{1},x_{2},...x_{n},t)} Полный запас энергии внутреннего состояния тел ( u ) {\displaystyle (u)} , вероятно, не может быть определён ни на каком уровне развития естествознания, но это обстоятельство не ограничивает уровня общности и точности математических выражений термодинамики, так как в эти соотношения входят лишь величины изменения внутренней энергии как функции состояния ( d u ) {\displaystyle (du)} , ( δ u ) {\displaystyle (\delta u)} . В связи с этим внутренняя энергия отсчитывается от произвольно выбранного уровня (например, 0℃и 760 ммрт. ст.). При построении термодинамики принимается также, что все возможные энергетические взаимодействия между телами сводятся лишь к передаче тепла и работы. Соответственно формулируется исходное выражение первого начала термодинамики по внешнему балансу как математическое выражение закона сохранения энергии : Изменение внутренней энергии тела или системы тел равно алгебраической сумме полученных (переданных) количеств тепла и работы или, что то же, тепло, полученное системой извне δ Q ∗ {\displaystyle \delta Q^{*}} последовательно обращается на изменение внутренней энергии системы d U {\displaystyle dU} и на выполнение (отдачу) внешней работы δ A {\displaystyle \delta A} . δ Q ∗ = d U + δ A ∗ {\displaystyle \delta Q^{*}=dU+\delta A^{*}} В этой формулировке слово последовательно, добавленное Н.И. Белоконем, имеет следующий смысл. Если представить себе процесс, в котором внутренняя энергия остается неизменной ( U = i d e m ) {\displaystyle (U=idem)} , то вышеприведённое выражение первого начала (без слова последовательно) будет прочитано так: Тепло, полученное телом или системой, обращается на выполнение внешней работы. Такое утверждение верно лишь в том смысле слова, что численные величины тепла и работы равны. В действительности, положительная работа системы выполняется зa счёт изменения её деформационных координат (например, за счёт увеличения объёма), а подвод тепла лишь компенсирует происходящее при этом уменьшение внутренней энергии (уменьшение, эквивалентное выполненной внешней работе), так что в конечном итоге внутренняя энергия системы оказывается не изменившейся. Предупредительное указание (последовательно) предназначено для восстановления условной картины последовательного снижения и восстановления уровня внутpeннейэнepгии при сопутствующем изменении потенциального состояния системы. Знаки работы и тепла в уравнениях первого начала термодинамики: A > 0 {\displaystyle A>0} — выполнение рабочим телом положительной работы; Q > 0 {\displaystyle Q>0} — сообщение тепла рабочему телу.
Общий случай — δ A i = ∑ F i d x i {\displaystyle \delta A_{i}=\sum F_{i}dx_{i}} Простое тело — δ A = P d V {\displaystyle \delta A=PdV} Выражения первого начала классической термодинамики действительны лишь для обратимых процессов. Это обстоятельство резко ограничивает возможности последующего развития принципов и практических приложений расчётных уравнений классической термодинамики. Поскольку все реальные процессы являются необратимыми, представляется целесообразным обобщить исходное уравнение первого начала термодинамики для обратимых и необратимых процессов. С этой целью Н.И. Белоконь, не снижая высокой степени общности исходных выражений первого начала, предложил для последующего развития основных принципов и расчётных уравнений термодинамики развернуть в них также выражения внешней работы. Для этого он ввёл понятие эффективной работы — δ A ∗ {\displaystyle \delta A^{*}} , равной разности термодинамической работы δ A i = ∑ F i d x i {\displaystyle \delta A_{i}=\sum F_{i}dx_{i}} и необратимых потерь δ A ∗∗ {\displaystyle \delta A^{**}} δ A ∗ = δ A − δ A ∗∗ {\displaystyle \delta A^{*}=\delta A-\delta A^{**}} Потерянная в необратимых процессах работа δ A ∗∗ {\displaystyle \delta A^{**}} превращается в тепло внутреннего теплообмена тела δ A ∗∗ {\displaystyle \delta A^{**}} ; это тепло возвращается рассматриваемому телу или передается телам внешней системы, причём соответственно уменьшается итоговая величина подвода тепла извне:δ A ∗∗ = δ Q ∗∗ {\displaystyle \delta A^{**}=\delta Q^{**}} Полное количество тепла, полученное телом δ Q {\displaystyle \delta Q} , характеризует термодинамический (приведённый), теплообмен тела и определяется как сумма двух величин — тепло, подведённое извне δ Q ∗ {\displaystyle \delta Q^{*}} , и тепло внутреннего теплообмена δ Q ∗∗ {\displaystyle \delta Q^{**}} : δ Q = δ Q ∗ + δ Q ∗∗ {\displaystyle \delta Q=\delta Q^{*}+\delta Q^{**}} 8. Цикл Карно— это обратимый круговой процесс, состоящий из двух адиабатических и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу и обменивается теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником. КПД для идеального газа— Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты
где Количество отдаваемой холодильнику теплоты
Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие
Аналогично для состояний 2 и 3 должно вытекать условие
Разделив одно соотношение на другое, приходим к условию замкнутости цикла
Теперь подставляя
В результате получим формулу для КПД цикла Карно:
9. Термодинамическая энтропияS {\displaystyle S} , часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работытепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций). Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Значимость данной величины для физики обусловлена тем, что наряду с температурой её используют для описания термических явлений и термических свойств макроскопических объектов. Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. д.; примерами термических явлений служат термическое расширение,пироэлектричество, электрокалорический эффект, теплопроводность, изменение агрегатного состояния — кристаллизация и замерзание, плавление и таяние, испарение, кипение, сублимация (возгонка), конденсация и другие процессы. 10. Второе начало термодинамики (второй закон термодинамики) устанавливает существование энтропии[1] как функции состояниятермодинамической системы и вводит понятие абсолютной термодинамической температуры[2], то есть «второе начало представляет собой закон об энтропии»[3] и её свойствах[4]. В изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах[3]), достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии)[5][6][2]. Встречающиеся в литературе различные формулировки второго начала термодинамики являются частными следствиями закона возрастания энтропии[5][6]. Второе начало термодинамики позволяет построить рациональную температурную шкалу, не зависящую от произвола в выборе термометрического свойства и способа его измерения[7].
11. Давление жидкости – физическая величина, определяемая нормальной силой, действующей со сто роны жидкости на единицу площади.P=∆F/∆SЗаконПаскаля:Давление в любом месте покоящейся жид кости одинаково по всем направлениям, причем давление одинаково передается по всему объему. Закон Архимеда:На тело, погруженное в жидкость (газ) действует со стороны этой жидкости (газа) вы талкивающая сила, направленная вверх и равная весу вытесненной телом жидкости. Fa=ρgVНесжимаемая жидкость – это жидкость, зависимость плотности которой от давления в данной задаче можно пренебречь.Гидростатическое давление. Если жидкость несжимаема, тогда при попереч ном сечении S столба жидкости, его высоте h, плотности ρ вес равен p=ρgSh, а давление на нижнее основание P=p/S=ρgh. 36. Ур-е неразрывности. Поток, линии тока, трубка тока, стационарное течение. Течение – движение жидкости.Поток – совокупность частиц, движущейся жидкости. Л За время ∆t через сечение S проходит объем жидкости V=ρυ∆t. Если жидкость несжимаема, то через площадь S1 за единицу времени пройдет такой же объем жидкости, как и через S2, тогда S1*υ1=S2*υ2 или S*υ=const – уравнение неразрывности. 12. Движение жидкостей называется течением,а совокупность частиц движущейся жидкости — потоком.Графически движение жидкостей изображается с помощью линий тока,которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы. Часть жидкости, ограниченную линиями тока, называют трубкой тока.Течение жидкости называется установившимся(или стационарным),если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.
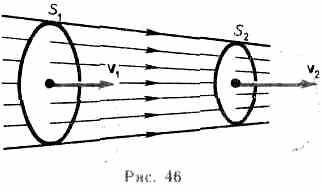
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 46). За время Dt через сечение S проходит объем жидкости SvDt; следовательно, за 1 с через S1 пройдет объем жидкости S1v1, где v1 — скорость течения жидкости в месте сечения S1. Через сечение S2 за 1 с пройдет объем жидкости S2v2, где v2 — скорость течения жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (r=const), то через сечение S2пройдет такой же объем жидкости, как и через сечение S1, т. е. S1v1= S2v2=const (29.1) Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (29.1) называется уравнением неразрывностидля несжимаемой жидкости. Статическое давление (рст)– это давление, зависящее от запаса потенциальной энергии газовой или жидкостной среды; определяется статическим напором. Оно может быть избыточным или вакуумметрическим, в частном случае может быть равно атмосферному. Динамическое давление (рд)– это давление, обусловленное скоростью движения потока газа или жидкости. 13. Закон Торричелли показывает, что при истечении идеальной нестискувальнои жидкости из щели в боковой стенке или на дне сосуда жидкость приобретает скорость тела, падающего с определенной высоты. С помощью этого можно вычислить максимальный уровень утечки жидкости из сосуда. Для подтверждения можно воспользоваться законом Бернулли, выведя из него формулу Торричелли: ρgh + p 0 = (pV2) / 2 + p 0, где p0 - атмосферное давление, h - высота столба жидкости в сосуде, V - скорость истечения жидкости. Отсюда V = √ 2gh. 5) Пульверизатор В пульверизаторе применяется главный следствие закона Бернулли: с ростом скорости происходит рост динамического давления и падение статического давления. В капилляры пульверизатора вдувается воздух или пар. Вдувание снижает атмосферное давление в капилляре, и жидкость из баллона пульверизатора под действием большего атмосферного давления поднимается капилляром. Там она раздробляется струей воздуха.
14. При изучении свойств рабочего тела а технической термодинамике вводят понятие идеального газа. Под идеальным газом понимают такой газ, у которого отсутствуют силы сцепления между молекулами, а молекулы представляют собой материальные точки, объём которых бесконечно мал по сравнению с объёмом, занимаемым газом. Реальный газ отличается от идеавльного тем, что у него молекулы имеют конечный объём и между ними действуют силы сцепления. Газообразные продукты сгорания топлива, являясь рабочим телом в д. в. с. по своим свойствам близки к идеальным газам, поэтому в тепловых расчётах допустимо считать газообразные продукты сгорания идеальными газами. |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 278. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
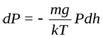 (9.50)
(9.50)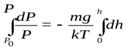 ,
, 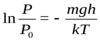
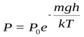 (9.51) — барометрическая формула.
(9.51) — барометрическая формула.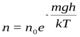 (9.52)
(9.52)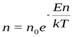 (9.53)
(9.53)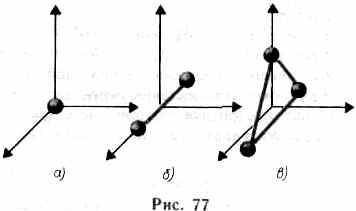
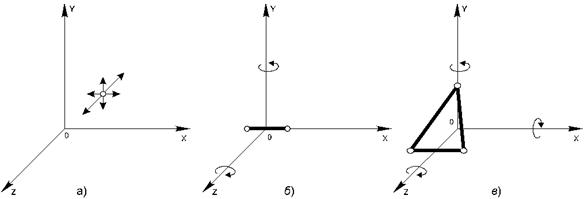
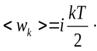 (20.1)
(20.1)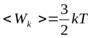 . Этот вывод согласуется с выражением (15.25). Действительно, ввиду хаотичности теплового движения молекул кинетическая энергия каждой из них равномерно распределяется между тремя степенями свободы, так что в среднем на каждую степень свободы приходится энергия, равнаяkT/2.
. Этот вывод согласуется с выражением (15.25). Действительно, ввиду хаотичности теплового движения молекул кинетическая энергия каждой из них равномерно распределяется между тремя степенями свободы, так что в среднем на каждую степень свободы приходится энергия, равнаяkT/2.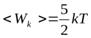 .
.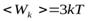 .
. равно работе
равно работе  , совершаемой газом при переходе из состояния 1 в состояние 2.(рис 2)
, совершаемой газом при переходе из состояния 1 в состояние 2.(рис 2) 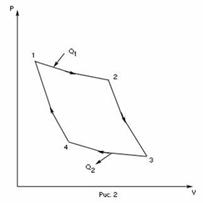 Эта работа равна
Эта работа равна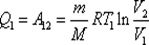 ,
, – масса идеального газа в тепловой машине.
– масса идеального газа в тепловой машине.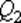 равно работе
равно работе 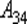 , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
, затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна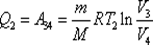 .
. .
.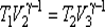 .
.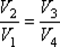 .
.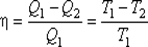 . (2)
. (2)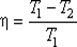
 иyии тока – линия, в каждой точке которой каса тельная к ней совпадает по направлению с вектор ом скорости в данный момент времени (используются для графического изображения жидкости). Линии тока проводятся так, чтобы густота их была больше там, где больше скорость движения жидкости.Трубка тока – часть жидкости, ограниченная линиями.Стационарное течение это течение жид кости, при котором форма и расположение линии тока, а также знак скоростей в каждой точке не меняется со временем.Ур-е неразрывности для нес жимаемойжидкости:Рассмотрим трубку тока, выбрав два сеченияS1, S2 перпендикулярные направлению скоростей.
иyии тока – линия, в каждой точке которой каса тельная к ней совпадает по направлению с вектор ом скорости в данный момент времени (используются для графического изображения жидкости). Линии тока проводятся так, чтобы густота их была больше там, где больше скорость движения жидкости.Трубка тока – часть жидкости, ограниченная линиями.Стационарное течение это течение жид кости, при котором форма и расположение линии тока, а также знак скоростей в каждой точке не меняется со временем.Ур-е неразрывности для нес жимаемойжидкости:Рассмотрим трубку тока, выбрав два сеченияS1, S2 перпендикулярные направлению скоростей.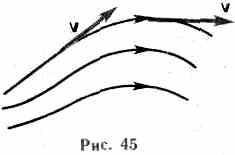
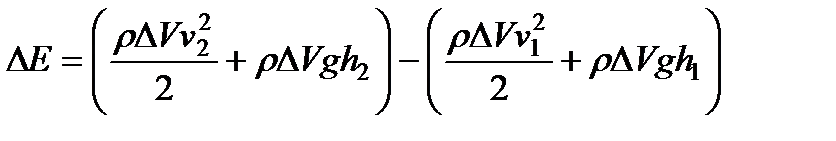 (98)
(98)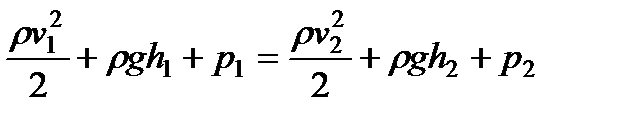 . (100)
. (100)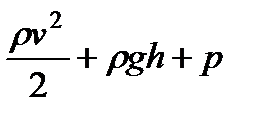 имеет одинаковое значение. В соответствии со сделанными нами при его выводе предположениями уравнение (100) становится вполне точным лишь при стремлении поперечного сечения S к нулю, т. е. при стягивании трубки тока в линию. Таким образом, величины р, v и h, фигурирующие в левой и правой частях уравнения (100), следует рассматривать как относящиеся к двум произвольным точкам одной и той же линии тока.
имеет одинаковое значение. В соответствии со сделанными нами при его выводе предположениями уравнение (100) становится вполне точным лишь при стремлении поперечного сечения S к нулю, т. е. при стягивании трубки тока в линию. Таким образом, величины р, v и h, фигурирующие в левой и правой частях уравнения (100), следует рассматривать как относящиеся к двум произвольным точкам одной и той же линии тока.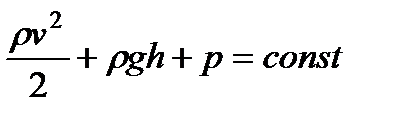 (101)
(101)