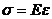Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Коэффициент Пуассона (коэффициент поперечных деформаций)Стр 1 из 2Следующая ⇒ РАБОТА №1. Определение механических свойств горных пород и грунтов на образцах
Цель работы: получение студентами навыков определения механических свойств горных пород в лабораторных условиях; ознакомление со статистическими методами обработки и оценки полученных экспериментальных данных; изучение методов учета влияния трещиноватости массива на механические свойства горных пород.
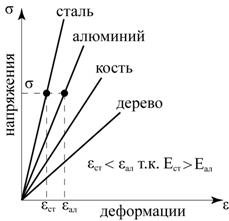
Общие сведения Горные работы сопровождаются процессами деформирования и разрушения пород (потери несущей способности). Для правильного решения различных горнотехнических задач, выбора параметров крепи выработок, размеров целиков и других ответственных элементов систем разработки, инженеры должны иметь необходимую информацию о свойствах горных породах, слагающих массив. Горные породы чрезвычайно разнообразны и обладают широким спектром различных свойств, среди которых в рамках данной работы можно выделить две отдельные группы – прочностные и деформационные свойства. К прочностным свойствам горных пород относятся пределы прочности на сжатие, на изгиб, на растяжение, на сдвиг (коэффициент сцепления); к деформационным – модуль Юнга (модуль деформаций), коэффициент Пуассона. Для определения указанных свойств в лабораторных условиях используются образцы горных пород. Они могут иметь как строго определенную геометрическую форму (призматические, цилиндрические) с заданным соотношением высоты и ширины, так и произвольную форму (рис.1).
Рис.1 Формы образцов для испытаний на определение механических свойств горных пород а – цилиндрическая; б – призматическая; в – произвольная 
Образцы изготовляют выбуриванием или выпиливанием на камнерезной машине из штуфов и кернов, их торцевые поверхности шлифуют на шлифовальном станке. В зависимости от формы образца методы определения свойств горных пород могут отличаться, однако наибольшая точность достигается при испытании образцов правильной формы. Для определения указанных механических свойств горных пород используются гидравлические, механические или ручные прессы (рис.2). Испытательные машины могут сильно отличаться размерами и конструкцией, но по существу все они представляют собой приспособления для приложения к образцам нагрузки, которую можно точно измерять (как и деформации образца).
Рис.2 Прессы для испытания образцов горных пород на прочность
Напряжение в образце вычисляется путем деления нагрузки, регистрируемой на каждой стадии испытаний по шкале динамометра, на площадь поперечного сечения образца. Сжатие образца под действием нагрузки (а следовательно, деформация материала) обычно измеряется с помощью экстензометра – чувствительного устройства, которое крепится к двум точка образца.
Рассмотрим более подробно основные механические свойства горных пород. 1. Пределы прочности горных пород на сжатие σсж и на растяжение σр. Под термином «прочность породы» понимают ее способность сопротивляться различным по интенсивности и характеру силовым воздействиям, не разрушаясь. При приложении к образцу горной породы сжимающей (растягивающей) нагрузки, он начинает деформироваться и при достижении нагрузкой некоторых предельных значений разрушается. Напряжения, действующие в образце на момент его разрушения, называются пределом прочности горной породы на сжатие (растяжение). Из курса механики известно, что напряжения являются мерой внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий, и определяются из соотношения силы и площади поверхности, на которой действует эта сила. В случае приложения нагрузки к образцу горной породы напряжения в нем можно найти из выражения
где σобр– напряжения в образце, Па; F - нагрузка, приложенная к образцу, Н; Sобр - площадь поперечного сечения образца, м2. Если в выражение (1) подставить значение предельной нагрузки на образец, то можно вычислить предел прочности породы на сжатие (растяжение)
где [σсж(р)]– предел прочности горной породы на сжатие (растяжение), Па; Fпред - предельная сжимающая (растягивающая нагрузка), Н; Sобр - площадь поперечного сечения образца до начала деформации, м2. Пределы прочности горных пород варьируются в широких пределах (табл. 1) []. Для всех типов горных пород предел прочности на сжатие превышает (в большинстве случаев – значительно) предел прочности на растяжение. Таблица 1
Пределы прочности на сдвиг и на изгиб определяются при приложении к образцам срезающих или изгибающих нагрузок соответственно.
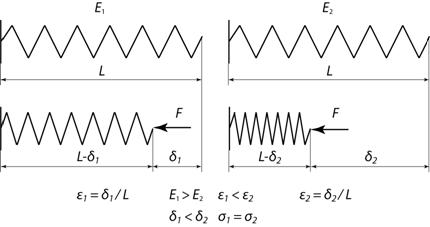
3. Модуль общей деформации – характеристика, показывающая, как деформируется материал под действием нагрузки при данном напряженном состоянии. Представим, что имеются две пружины различной жесткости E1 и E2, причем E1 > E2 (рис. 3). При сжатии пружин силой F пружины сократятся на величины δ1 и δ2 соответственно, причем δ1 < δ2, так как первая пружина более жесткая, чем вторая.
Рис. 3 Пружины с различной жесткостью под действием одинаковой силы F Пружина слева обладает большей жесткостью, чем пружина справа, поэтому и сжимается на меньшую величину при приложении к обеим пружинам одинаковой силы
Соотношение При приложении к пружине силы F в ней возникают напряжения σ и деформации ε (изменение размеров и некоторых случаях – объема). Между возникающими в пружине напряжениями и деформациями существует прямая пропорциональная зависимость, называемая законом Гука (закон упругого деформирования):
где σ – действующие в пружине напряжения, Па; E – коэффициент жесткости пружины или модуль Юнга, Па; ε – деформации пружины. Из соотношения видно, что при приложении одной и той же нагрузки к пружинам с различной жесткостью E деформации той пружины будут меньше, у которой жесткость выше. В первом приближении можно утверждать, что процессы, подобные рассмотренным на пружинах, действуют и в горных породах. При приложении силы к образцу горной породы происходит его сжатие, величина которого так же, как и в случае с пружиной, определяется модулем Юнга (в большинстве случаев при испытаниях горных пород речь идет не о модуле Юнга, а о модуле общих деформаций, см. ниже). Как указывалось выше, испытательное оборудование позволяет довольно просто измерить напряжения и деформации в образце, которые возникают по мере того, как мы увеличиваем нагрузку. Графическое изображение зависимости напряжений от деформаций называется кривой деформирования. Если материал подчиняется закону Гука, то кривая имеет вид, представленный на рис. 4 (стоит отметить, что горные породы деформируются по упругому закону только при очень малых напряжениях, при повышении же нагрузки закон деформирования становится совсем иным, о чем будет рассказано чуть ниже). Из графика на рис. 4 и выражения (4) видно, что тангенс угла наклона кривой деформирования tgα = σ / ε = E.
Рис. 4 Кривая деформирования Тангенс угла наклона кривой деформирования является параметром материала, который называется модулем Юнга и обозначается E
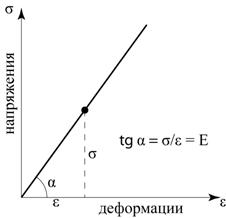
На рис.5 для сравнения представлены кривые деформирования различных материалов и горных пород (на начальном этапе деформирования). Видно, что при одном и том же уровне напряжений различные материалы деформируются по-разному. Чем круче угол наклона кривой (чем больше модуль Юнга Е), тем жестче материал, которому она соответствует.
Рис. 5 Кривые деформирования различных материалов и горных пород (на начальном Широкий спектр свойств различных материалов определяет и существенные различия в их поведении при приложении нагрузок. Например, из графика видно, что при одинаковом уровне напряжений деформации стали меньше деформаций алюминия, что предопределяется ее большей жесткостью (большим модулем Юнга).
Однако, как упоминалось выше, при повышении напряжений закон деформирования горных пород начинает отличаться от упругого и прямая зависимость между напряжениями и деформациями нарушается, как показано на рис. 6. Не вдаваясь пока в подробности, почему так происходит, отметим, что в этом случае вместо модуля Юнга вводят понятие модуля общих деформаций. Отличие их заключается в том, что модуль Юнга учитывает деформации материала только в так называемой упругой зоне (см. рис. 6), в то время как модуль общих деформаций позволяет определить величину деформации за пределами зоны упругости. Аналогично модулю Юнга, модуль деформаций определяется как угол наклона кривой соединяющей начало координат и точку на кривой деформирования. Видно, что модуль деформаций может иметь множество значений в зависимости от того, какая точка на графике выбрана. Каждая точка на графике соответствует определенному напряженному состоянию образца и для каждой конкретной горно-геомеханической задачи эта точка (и соответственно значение модуля деформаций) выбирается исследователем самостоятельно, исходя и целей и задач исследования.
Рис. 6 Модуль общей деформации
Коэффициент Пуассона (коэффициент поперечных деформаций)
Зачем же нам необходимо знать эти свойства горных пород? Попробуем на простом примере рассмотреть, как знание этих свойств позволит решить реальную практическую задачу. Представим себе подземное сооружение, которое построено на некоторой глубине от поверхности земли и горному инженеру поставлена задача определить, на сколько сместиться контур выработки, и ее устойчивость. Как было показано выше модуль упругости позволяет нам определить, как и на сколько деформируется материал (меняет форму и объем) под нагрузкой. В качестве нагрузки в данном случае будут выступать напряжения, которые сформировались в горном массиве, (определение напряженно-деформированного состояния массива будет рассмотрено в работе 4-6). И теперь зная величину модуля упругости, которая предварительно была определена на образцах в лаборатории, и напряженное состояние массива, по закону Гука, можно найти величину деформации горного массива вокруг выработки и как следствие величину смещения контура выработки. Устойчивость выработки можно оценить, сравнив прочность горных пород, полученных по результатам лабораторных испытаний, с величиной напряжений вокруг выработки. Не вдаваясь в подробности (работа 2, 3) можно сказать, что выработка будет устойчивой, если величина напряжений не превысит прочности породы. Итого для решения простейшей задачи геомеханики нам необходимо как минимум знать, плотность горной породы, ее деформационные и прочностные характеристики. В предыдущих параграфах были даны основные понятия о свойствах горных пород, без привязки их к горному массиву и рассматривались как изотропное не нарушенное тело. Но горные породы не однородны по своей структуре, и их свойства сильно зависят от нарушенности горного массива, то есть его трещиноватости. Рассмотрим, как влияет трещиноватость на свойства пород в горном массива и почему при испытании образцов горных пород получаются характеристики отличные от их характеристик в массиве.
Порядок проведения работы |
||||||||||||||||||
|
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 305. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||
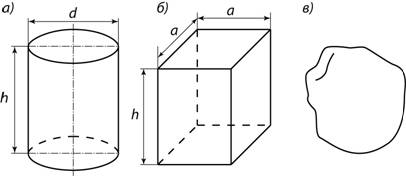
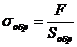
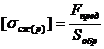
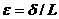называется относительной деформацией пружины и показывает, насколько в долях от первоначального размера изменилась длина пружины (здесь δ – величина сокращения пружины, м; L – первоначальная длина пружины, м).
