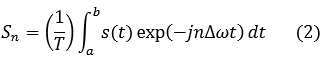Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие собственных функцийУдобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных по координатам. Предположим, что начальная функция является линейной комбинацией функций синуса и косинуса: 𝑠(𝑥) = 𝐴sin(𝑥) + 𝐵cos(𝑥) Осуществим произвольный сдвиг функций с аргументом на величину h. При этом получаем: 𝑠(𝑥 + ℎ) = 𝐶sin(𝑥) + 𝐷cos(𝑥) 𝐶 = 𝐴cos(ℎ) − 𝐵sin(ℎ) 𝐷 = 𝐴sin(ℎ) + 𝐵cos(ℎ) где коэффициенты C и D, как и в начальном выражении коэффициенты А и В, не зависят от аргумента, при этом C2+D2=А2+В2. Таким образом, при произвольном переносе функции с аргументом (а равно и при интегрировании, дифференцировании и других линейных преобразованиях) любую линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций. Экспоненциальный комплексный запись гармонических функций делает это свойство еще нагляднее. Для произвольной гармонической функции имеем: cos(𝜔𝑡 − 𝜑) = 𝐴cos(𝜔𝑡) + 𝐵sin(𝜔𝑡) де𝐴=cos(𝜑),𝐵=sin(𝜑),𝜑–начальный фазовый угол колебания при t = 0. Переходя к комплексной записи данной функции с использованием тождеств Эйлера:
Получаем: Где,  Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса с использованием экспоненциальных функций:
Для операции дифференцирования:
Для операции интегрирования:
В общей форме для любых операций преобразования:
У специалистов-практиков существует предубеждение против использования комплексных функций с их мнимыми частотами. Поэтому в дальнейшем будем использовать и вещественные функции, и их комплексные аналоги, по крайней мере, до тех пор, пока простота и удобство использования последних не станет очевидной.
Ряды Фурье
Разложению в ряды Фурье подвергаются периодические сигналы. Периодическую функцию любой формы, заданную на интервале одного периода Т = b - a ту, что удовлетворяет на этом интервале условиям Дирехле (ограниченная, кусочно - непрерывная, с конечным числом разрывов 1-го рода), можно представить в виде ряда Фурье:
Ряд Фурье является ансамблем комплексных экспонент exp(jnΔωt) с частотами, образующими арифметическую прогрессию. Функцию весовых коэффициентов S(nΔω) принято называть комплексным спектром периодического сигнала или Фурье-образом функции s(t). Спектр периодического сигнала является дискретной функцией, поскольку он определен только для целых значений n с шагом по частоте, обратным к периоду: Δω = 2π/Т (илиΔf = 1/T). Первую частотную составляющую спектра при n = 1, равную ω1 = 1*Δω = 2π/T (или f1 = 1/T), называют основной частотой сигнала (первой гармоникой), другие частоты дискретного спектра n1 при n>1 называют гармониками сигнала. Значение S(nω1) по положительным и отрицательным значениях n являются комплексно сопряженными. С чисто математических позиций множество функций exp(jnΔωt) образует бесконечномерный базис линейного пространства L2[a, b] ортогональные синус-косинусных функций, а коэффициенты Sn по (2) являются проекциями сигнала s(t) на эти базисные функции. Соответственно, сигнал s(t) в форме ряда Фурье (1) - это бесконечномерный вектор в пространстве L2[a, b]. Подынтегральную функцию экспоненты в выражении (2) с использованием тождества Эйлера exp(-jωt)=cos(ωt) – j*sin(ωt) можно разложить на косинусную и синусную составляющие и выразить комплексный спектр в виде действительной и мнимой частей:
На рис. 4.1.1 приведен пример периодического сигнала (прямоугольный импульс на интервале (1-3.3), повторяющийся с периодом Т=40) и форма действительной и мнимой части его спектра. Обратим внимание, что действительная часть спектра является четным относительно нуля функцией A(nDw) = A(- nDw), поскольку при вычислении значений A(nDw) по формуле (4) используется парная косинусна функция cos(nDwt) = cos(-nDwt). Мнимая часть спектра является нечетной функцией B(nDw) = -B(-nDw), поскольку для ее вычисления по (5) используется нечетное синусная функция sin(nDwt) = - sin(-nDwt).
рис. 18 Сигнал и его комплексный спектр. Комплексные числа дискретной функции (3) могут быть представлены в виде модулей и аргументов комплексной экспоненты, что дает следующую форму записи комплексного спектра: Sn = Rn exp(jjn), (4.1.3') Rn2≡ R2(nDw) = A2(nDw)+B2(nDw), jn ≡ j (nDw) = arctg(-B(nDw)/A(nDw)).
рис. 19 Модуль и аргумент спектра. Модуль спектра R(n)wD называют двусторонним спектром амплитуд, а аргумент спектра (последовательность фазовых углов (jn))wD - двусторонним спектром фаз. Спектр амплитуд всегда является четной функцией: R(n) =wDR(- n),wD а спектр фаз нечетную(j: n(-j) = -wDn).wD Пример спектра в амплитудном и фазовом представлении для сигнала, показанного на рис. 18, приведен на рис. 19. При рассмотрении спектра фаз следует учитывать периодичность 2p угловой частоты (при уменьшении фазового значения до величины меньше p- происходит сброс значения - 2p).
рис. 20 Ортогональность функций Если функция s(t) является четной, то все значения B(nwD) по (5) равны нулю, поскольку четные функции ортогональные синусным гармоникам и подынтегральное произведение s(t) - sin(nwDt) дает нулевой интеграл. Следовательно, спектр функции будет представлен только вещественными коэффициентами. Наоборот, при нечетности функции s(t) обнуляются все значения коэффициентов А(нечетные функции ортогональным косинусным гармоникам) и спектр является чисто мнимым. Этот фактор не зависит от выбора границ задачи периода функции на числовой оси. На рис. 20(А) можно наглядно видеть ортогональность первой гармоники синуса и четной функции, а на рис. 20(В) соответственно косинуса и нечетной функции в пределах одного периода. Учитывая кратность частот следующих гармоник первой гармонике спектра, ортогональность сохраняется для всех гармоник ряда Фурье. При n = 0 имеем Во = 0, и получаем постоянную составляющую сигнала:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 253. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 - величина, комплексно сопряженная с С. Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jωt), можно рассматривать вторую функцию ехр(–jωt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является чисто математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию.
- величина, комплексно сопряженная с С. Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jωt), можно рассматривать вторую функцию ехр(–jωt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является чисто математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию. , где
, где  - собственное значение операции переноса, независимое от переменной.
- собственное значение операции переноса, независимое от переменной.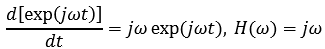

 где T[.] – произвольный линейный оператор, Н(ω) – собственное значение операции, независимо от аргумента.
где T[.] – произвольный линейный оператор, Н(ω) – собственное значение операции, независимо от аргумента. ,
,