
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы линейного программирования и оптимизацииЛабораторная работа № 2 Цель работы: научиться решать экономические задачи оптимизации средствами линейного программирования в Excel.
Линейное программирование - область математического программирования, посвященная теории и методам решенияэкстремальных задач, характеризующихсялинейной зависимостьюмеждупеременными. Линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания. Если же переменныe в зависимость входят не в первой степени или с ними выполняются другие действия, то функции являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной. Задача оптимизации формулируется как нахождение оптимального значения целевой функции для определенной области изменения ее аргументов, которая задается системой ограничений. Для решения задачи формируется ее математическая модель, в электронную таблицу вносятся нужные данные, осуществляется поиск оптимального решения. Для решения оптимизационных задач строят математические (функциональные) модели, которые решаются методами линейного программирования. Разработайте математические модели и решите в Microsoft Excel задачи: Задача № 1.Задача о пищевом рационе. Пусть имеется некоторый набор продуктов. Стоимость единицы каждого из них известна и соответственно равна c1, c2, …,cn. Из этих продуктов необходимо составить пищевой рацион, который должен содержать: · не менее b1 единиц питательного вещества R1, · не менее b2 единиц питательного вещества R2,  · …………………………………………………… · не менее bm единиц питательного вещества Rm. Известно, что единица каждого продукта содержит aij единиц питательного вещества Rj, где Найти: оптимальный рацион питания, чтобы обеспечить необходимое содержание в нём всех питательных веществ и наименьшую стоимость. Составим математическую модель задачи о пищевом рационе. Для этого обозначим через xj количество продукта j необходимое для составления рациона Тогда необходимо найти план X=(x1,x2,…,xn), удовлетворяющий системе ограничений
(критерий оптимальности – минимальная стоимость рациона). Очевидно, что неизвестные задачи должны удовлетворять условиям неотрицательности:
Как видно, составленная математическая модель задачи о пищевом рационе − это задача линейного программирования, записанная в симметричной форме (стандартная задача минимизации). Составьте информационную модель задачи в Excel (табл. 1). В ячейки «Ограничения» и «Целевая функция» надо ввести формулы, описанные в математической модели (после ввода формул там появятся нулевые значения). Для решения задачи нужно запустить «Поиск решения» и ввести требуемые параметры для него.
Таблица 1 – Информационная модель задачи о рационе в Excel
Задача № 2. Из одного города в другой ежедневно отправляются пассажирские и скорые поезда. В таблице указано количество вагонов в поездах различного типа и максимальное число пассажиров, на которое рассчитан вагон. Сгенерируйте самостоятельно целые числа для условия задачи все, кроме числа пассажиров, помещающихся в вагоны, и решите задачу с собственным условием. Найти: число скорых Х1 и пассажирских Х2 поездов, которые необходимо формировать ежедневно из имеющегося парка вагонов, чтобы число перевозимых пассажиров было максимальным.
Задача № 3. Четверо рабочих могут выполнять четыре вида работ. Стоимости Сij выполнения i-м рабочим j-й работы приведены в таблице.
Сгенерируйте самостоятельно целые числа для условия задачи и решите задачу с собственным условием. Найти: такой план работ, чтобы все работы были выполнены, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 254. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


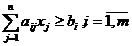 и обеспечивающей целевой функции минимальное значение
и обеспечивающей целевой функции минимальное значение
