
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лабораторная работа №8. Решение задачи нелинейного программирования методами Лагранжа и приведенного градиента ВулфаПри решении использовать методы неопределенных множителей Лагранжа, приведенного градиента Вулфа. Пример. Требуется найти максимальное значение заданной целевой функции
6.8.1 Метод неопределенных множителей Лагранжа Метод реализован в Lagrang.pas.
Входные данные. Описание типов.
TKvadrF = Record c : Array of Array of Real; D : Array of Real; End – запись для хранения целевой функции. TOgr = Record A : Array of Array of Real; B : Array of Real; End запись для хранения системы ограничений. TSyst = Array of Array of Real – для хранения системы ограничений при переходе к задаче линейного программирования. Используемые глобальные переменные: - KF : TKvadrF – хранит целевую функцию; - Ogr : TOgr – хранит систему ограничений. - m,n : Integer – количество ограничений и переменных соответственно; - Syst : TSyst – хранит новую систему ограничений. Описаны следующие функции. Функция Function Lagr(Var X : Array of Real;Var Res : Byte) : Real – реализует метод неопределенных множителей Лагранжа. Возвращает оптимальное значение функции. Параметры функции: - X – на выходе получает оптимальную точку; - Res –признак решения (на выходе возвращает 1, если задача решена и ноль, если задача неразрешима). Процедура Procedure SM (Syst: TSyst; m, n: Integer; Var X: Array of Real; Var Res: Byte) – решает задачу линейного программирования методом искусственного базиса. Параметры функции: - Syst – система ограничений; - m и n – количество ограничений и переменных соответственно; - X – на выходе содержит оптимальную точку; - Res – признак решения (на выходе возвращает 1, если задача решена и ноль, если задача неразрешима). Текст программы. {Метод неопределенных множителей Лагранжа}  {Расчитан на решение задач выпуклого программирования. В вызывающей программе должна быть определена квадратичная форма KF, ограничения Ogr, а также пере- менные n и m, хранящие число переменных и ограничений.} unit Lagrang; interface uses dialogs,SysUtils; Type {Тип квадратичная форма.Задается целевая функция} TKvadrF = Record c : Array of Array of Real; D : Array of Real; End; {Тип ограничений.Задаются ограничения для данной задачи} TOgr = Record A : Array of Array of Real; B : Array of Real; End;
{Производные функции Лагранжа по всем переменным.} TSyst = Array of Array of Real;
Var {KF,Ogr,m и n необходимо определить в вызывающей програмее} KF : TKvadrF; Ogr : TOgr; m,n : Integer;//m - количество ограничений, //n - количество переменных Syst : TSyst;
{Основная функция} Function Lagr(Var X : Array of Real;Var Res : Byte) : Real; //X - в эту переменную вернется оптимальное значение неизвестных //Res - вернет 1, если задача решена, 0 - если неразрешима Procedure SM(Syst : TSyst;m,n : Integer;Var X : Array of Real;Var Res : Byte);
implementation
Procedure SM; Var I,J : Integer; SystNew : TSyst;//Новая система с большим количеством // переменных чем в Syst mm,nn : Integer;//Новое количество переменных и ограничений A : Array of Array of Real;//Для хранения всех базисов Basis : Array of Integer;//Хранит номера векторов, вошедших в базис MV,Cbas,B,BCopy,Ocenki : Array of Real; //MV - Хранит коэффициены при каждой переменной в //целевой функции //CBas - Содержит коэффициенты при соответствующих //неизвестных в целевой функции //B - хранится опорный план //BCopy - временная переменная для вычисления B //Ocenki - хранит оценки Optim,ImeetResh : Boolean; //Optim - хранит информацию, оптимален ли план //ImeetResh - Хранит информацию, имеет ли задача решение min : Real;//вспомогательнач переменная VedStr,VedCol : Integer; //VedCol - ведущий столбец //VedStr - ведущая строка Begin SetLength(SystNew,n+m,n+m+n+m+n+1);//Определяется размернсть с учетом //дополнительных неизвестных в задаче For I:=0 to n+m-1 do For J:=0 to n+m-1 do SystNew[I,J]:=Syst[I,J]; //Заносятся старые значения
For I:=m+n to m+n+n-1 do SystNew[I-m-n,I]:=-1;//Вводятся переменные Vi, для //перехода к равенству в производных по x For I:=m+n+n to m+n+n+m-1 do SystNew[I-n-n,I]:=1;//Вводятся переменные Wi, для //перехода к равенству в производных по Lambda For I:=m+n+n+m to m+n+n+m+n-1 do SystNew[I-m-n-n-m,I]:=1; //Вводятся переменные //Zi, для введения искусственного базиса For I:=0 to n+m-1 do SystNew[I,n+m+n+m+n]:=Syst[I,n+m];//Копируются правые части
mm:=n+m; //Определяется новая размерность nn:=n+m+n+m+n;
SetLength(A,nn,mm); For I:=0 to nn-1 do //Заполнение матрицы базисов For J:=0 to mm-1 do A[I,J]:=SystNew[J,I];
SetLength(Basis,mm); For I:=0 to mm-1 do Basis[I]:=nn+I-mm;//В качестве базиса берутся искуственно //введенные вектора, то есть введенные последними SetLength(MV,nn); For I:=0 to nn-n-1 do MV[I]:=0; //Коэффициенты в новой целевой функции отличны For I:=nn-n to nn-1 do MV[I]:=-1;//от нуля только при искуственных переменных
SetLength(Cbas,mm); For I:=0 to mm-1 do Cbas[I]:=MV[Basis[I]];//Вводятся коэффициенты при переменных, //входящих в базисное решение SetLength(B,mm); For I:=0 to mm-1 do B[I]:=Syst[I,mm];//Начальное опорное решение SetLength(BCopy,mm);
SetLength(Ocenki,nn); For I:=0 to nn-1 do {Вычисление оценок} Begin Ocenki[I]:=0; For J:=0 to mm-1 do Ocenki[I]:=Ocenki[I]+Cbas[J]*A[I,J]; Ocenki[I]:=Ocenki[I]-MV[I]; End;
ImeetResh:=True; For I:=0 to nn-1 do //Выясняется, есть ли решение у данной задачи If Ocenki[I]<0 Then Begin Optim:=False;//Optim используется как вспомогательная переменная For J:=0 to mm-1 do Optim:=Optim Or (A[I][J]>0); ImeetResh:=ImeetResh and Optim; End;
Optim:=True; for I:=0 to nn-1 do If Ocenki[I]<0 Then Begin Optim:=False;Break;End; //Проверка на оптимальность If ImeetResh Then//Если имеет решение... Begin While (Not Optim) do//Пока не оптимально ... Begin min:=0; For I:=1 to nn-1 do//Вычисление минимальной оценки If Ocenki[I]<Ocenki[Round(min)] Then min:=I; VedCol:=Round(Min);//Ведущей столбец там, где оценка наименьшая
For I:=0 to mm-1 do// Находится первый положительный элемент в ведущем столбце If A[VedCol][I]>0 Then Begin min:=I;Break;End;
I:=Round(min+1); While I<=mm-1 do//Находится ведущая строка. //Она будет там, где отношение базисного Begin //элемента к положительному элементу ведущего //столбца будет минимальным If A[VedCol][I]>0 Then If (B[I]/A[VedCol][I])<(B[Round(min)]/A[VedCol][Round(min)]) Then Begin min:=I;End; Inc(I); End; VedStr:=Round(min);
BCopy:=Copy(B); For I:=0 to mm-1 do //Вычисление нового опроного решения If I<>VedStr Then// Если строка не ведущая, то вычисляется по // правилу прямоугольника B[I]:=(BCopy[I]*A[VedCol][VedStr]- A[VedCol][I]*BCopy[VedStr])/A[VedCol][VedStr] Else//Иначе вычисляется делением на ведущий элемент B[I]:=BCopy[I]/A[VedCol][VedStr];
For I:=0 to mm-1 do//Вычисление новых векторов A Begin If I<>VedStr Then//Если строка не ведущая For J:=0 to nn-1 do Begin//Правило прямоугольника A[J][I]:=(A[J][I]*A[VedCol][VedStr]- A[VedCol][I]*A[J][VedStr])/A[VedCol][VedStr]; End; End;
{Вычисление новых значений в ведущей строке} For I:=0 to nn-1 do If I<>VedCol Then A[I][VedStr]:=A[I][VedStr]/A[VedCol][VedStr]; A[VedCol][VedStr]:=1; Basis[VedStr]:=VedCol;//Замена в базисе Cbas[VedStr]:=MV[VedCol];//Новое значение в векторе Cbas
For I:=0 to nn-1 do//Вычисление новых оценок Begin Ocenki[I]:=0; For J:=0 to mm-1 do Ocenki[I]:=Ocenki[I]+Cbas[J]*A[I,J]; Ocenki[I]:=Ocenki[I]-MV[I]; End;
Optim:=True;//Проверка плана на оптимальность for I:=0 to nn-1 do If Ocenki[I]<0 Then Begin Optim:=False;Break;End;
End;{While}
For I:=0 to High(Basis) do If Basis[I]<=n-1 Then X[Basis[I]]:=B[I]; // For I:=0 to n-1 do X[I]:=B[I];//Оптимальная точка Res:=1;//Задача решена End Else Res:=0;//Задача неразрешима
End;
Function Lagr; Var I,J : Integer; Begin SetLength(Syst,n+m,n+m+1);{n+m так как производные по всем переменным x дают n, а по всем переменным Lambda дают m. Так как будут храниться и правые части, то вводится +1} {Заполняется система производных} For I:=0 to n-1 do Begin For J:=0 to n-1 do if I<>J Then Begin Syst[I,J]:=-KF.c[i,j];//Минус берется, т.к. в дальнейшем //придется менять знак End Else Begin Syst[I,I]:=-2*KF.c[I,I];//Вычисление производных второго порядка. End; For J:= n to m+n-1 do {Вычисляются производные подфункций вида Lambda*f(X1..Xn)} Syst[I,J]:=Ogr.A[J-n,I]; End;
For I:=n to m+n-1 do Begin For J:= 0 to n-1 do Syst[I,J]:=Ogr.A[I-n,J];//Минус не берется, т.к. в дальнейшем //придется менять знак
For J:=n to m+n-1 do Syst[I,J]:=0; End;
For I:=0 to n-1 do Syst[I,m+n]:=KF.D[I];//Формируются правые части // системы в произвоных по x For I:=n to m+n-1 do Syst[I,m+n]:=Ogr.B[I-n];//Формируются правые // части системы в произвоных по Lambda SM(Syst,m,n,X,Res);//Вызывается симплекс метод для дальнейшего // решения задачи Result:=0; For I:=0 to n-1 do//Вычисление оптимального значения функции For J:=I to n-1 do Result:=Result+KF.C[I,J]*X[I]*X[J];
For I:=0 to n-1 do Result:=Result+KF.D[I]*X[I]; End; end.
Результат работы программы. Оптимальное решение: x=(0.67,0.67). Оптимальное значение функции: 0,44. 6.8.2 Метод приведенного градиента Вулфа
Метод реализован в модуле Wolf.pas. Описание типов. TPoint = Array of Real; TPurposeFunction = Function (P: TPoint): Real; TVector = Array of Real; TMatrix = Array of Array of Real; TProisvod = Array of Function(P : TPoint) : Real. Используемые глобальные переменные. P: TPoint – хранит текущую точку. PF: TPurposeFunction – хранит целевую функцию. Proisvod: TProisvod – массив производных. d: TVector – служебная переменная. cc: TMatrix – первая часть квадратичной формы. dd: TVector – вторая часть квадратичной формы. Описание функций. Function Search (n, m: Integer; A: TMatrix): Real – реализует метод Вулфа. Параметры функции. m – количество ограничений. n – количество переменных. A –матрица коэффициентов системы ограничений. Текст программы. unit Wolf; interface Type TPoint = Array of Real; TPurposeFunction = Function(P : TPoint) : Real; TVector = Array of Real; TMatrix = Array of Array of Real; TProisvod = Array of Function(P : TPoint) : Real; Var P : TPoint; PF : TPurposeFunction; Proisvod : TProisvod; d : TVector; cc : TMatrix; dd : TVector;
Function Search(n,m : Integer;A : TMatrix) : Real;
implementation Uses Ravnomer_Search;
Function Optim(d : TVector) : Boolean; Var I : Integer; Begin Result:=True; For I:=0 to High(d) do Result:=Result and (d[I]=0);
End;
Procedure ObrMat (N : Byte; A : TMatrix; Var B : TMatrix ); Var i,j,k : Byte; Base : real; Begin for i:=0 to N-1 do for j:=0 to N-1 do if i=j then B[i][j]:=1 else B[i][j]:=0;
for k:=0 to N-1 do begin Base := A[k][k]; for i:=0 to N-1 do for j:=0 to N-1 do begin if (i<>k) and (j>k) then A[i][j] := A[i][j] - A[k][j]*A[i][k]/Base; if i<>k then B[i][j] := B[i][j] - B[k][j]*A[i][k]/Base; end; if Base<>1 then for i:=0 to N-1 do begin A[k][i] := A[k][i]/Base; B[k][i] := B[k][i]/Base; end; for i:=0 to N-1 do if i<>k then A[i][k] := 0; end; End;
Function func(x : Real) : Real; Var I,J : Integer; Begin Result:=0; For I:=0 to High(P)-1 do For J:=I to High(P)-1 do Result:=Result+cc[I,J]*(P[I]+d[I]*x)*(P[J]+d[J]*x); For I:=0 to High(P)-1 do Result:=Result+dd[I]*(P[I]+x*d[I]); End;
Function Search; Var BBObr : TMatrix; BB,NN,MatrixTemp : TMatrix; I,J,k,l : Integer; I1 : Array of Integer; I11 : Set of Byte; GradF,GradBF,Multipl,rT,dB,dN : TVector; Sum,Lambda : Real; f : Ravnomer_Search.FType; Res : Byte; PTemp : TPoint;
Begin SetLength(BB,m,m); SetLength(BBObr,m,m); SetLength(NN,m,n-m); SetLength(I1,m); SetLength(PTemp,n); SetLength(GradF,n); SetLength(GradBF,m); SetLength(Multipl,n); SetLength(rT,n); SetLength(dB,m); SetLength(dN,n-m); SetLength(d,n); SetLength(MatrixTemp,m,n-m);
f:=func; PTemp:=Copy(P); I11:=[]; For I:=0 to m-1 do Begin I1[I]:=0; For J:=0 to n-1 do If PTemp[J]>PTemp[I1[I]] Then Begin I1[I]:=J; End; PTemp[I1[I]]:=-3000000; I11:=I11+[I1[I]]; End; k:=0;l:=0; For I:=0 to n-1 do If I in I11 Then Begin For J:=0 to m-1 do Begin BB[J][k]:=A[J][I]; End; Inc(k); End Else Begin For J:=0 to m-1 do Begin NN[J][l]:=A[J][I]; End; Inc(l); End;
ObrMat(m,BB,BBObr);
For I:=0 to n-1 do GradF[I]:=Proisvod[I](P);
k:=0; For I:=0 to n-1 do If I in I11 Then Begin GradBF[k]:=Proisvod[I](P); Inc(k); End;
For I:=0 to m-1 do Begin Sum:=0; For J:=0 to m-1 do Sum:=Sum+GradBF[J]*BBObr[J][I]; Multipl[I]:=Sum; End;
For I:=0 to n-1 do Begin Sum:=0; For J:=0 to m-1 do Sum:=Sum+Multipl[J]*A[J][I]; rT[I]:=Sum; End;
For I:=0 to n-1 do rT[I]:=GradF[I]-rT[I];
k:=0; For I:=0 to n-1 do If Not (I in I11) Then Begin If rT[I]<=0 Then Begin dN[k]:=-rT[I]; End Else Begin dN[k]:=-P[I]*rT[I]; End; Inc(k); End;
For I:=0 to m-1 do For J:=0 to n-m-1 do Begin MatrixTemp[I,J]:=0; For k:=0 to m-1 do MatrixTemp[I,J]:=MatrixTemp[I,J]+BBObr[I,k]*NN[k,J]; End;
For I:=0 to m-1 do Begin dB[I]:=0; For J:=0 to n-m-1 do dB[I]:=dB[I]+MatrixTemp[I,J]*dN[J]; dB[I]:=-dB[I]; End;
k:=0;l:=0; For I:=0 to n-1 do If I in I11 Then Begin d[I]:=dB[k]; Inc(k); End Else Begin d[I]:=dN[l]; Inc(l); End;
For I:=0 to n-1 do If d[I]<0 Then Begin Lambda:=-P[I]/d[I];Break; End;
For I:=0 to n-1 do If (d[I]<0) and (-P[I]/d[I]<Lambda) Then Lambda:=-P[I]/d[I];
Lambda:=Ravnomer_Search.Search(0,Lambda,100,f,Res,0.001);
For I:=0 to n-1 do P[I]:=P[I]+Lambda*d[I]; For I:=0 to n-1 do If abs(P[I])<0.0001 Then P[I]:=0;
While not Optim(d) do Begin
PTemp:=Copy(P); I11:=[]; For I:=0 to m-1 do Begin I1[I]:=0; For J:=0 to n-1 do If PTemp[J]>PTemp[I1[I]] Then Begin I1[I]:=J; End; PTemp[I1[I]]:=-3000000; I11:=I11+[I1[I]]; End; k:=0;l:=0; For I:=0 to n-1 do If I in I11 Then Begin For J:=0 to m-1 do Begin BB[J][k]:=A[J][I]; End; Inc(k); End Else Begin For J:=0 to m-1 do Begin NN[J][l]:=A[J][I]; End; Inc(l); End;
ObrMat(m,BB,BBObr);
For I:=0 to n-1 do GradF[I]:=Proisvod[I](P);
k:=0; For I:=0 to n-1 do If I in I11 Then Begin GradBF[k]:=Proisvod[I](P); Inc(k); End;
For I:=0 to m-1 do Begin Sum:=0; For J:=0 to m-1 do Sum:=Sum+GradBF[J]*BBObr[J][I]; Multipl[I]:=Sum; End;
For I:=0 to n-1 do Begin Sum:=0; For J:=0 to m-1 do Sum:=Sum+Multipl[J]*A[J][I]; rT[I]:=Sum; End;
For I:=0 to n-1 do rT[I]:=GradF[I]-rT[I];
k:=0; For I:=0 to n-1 do If Not (I in I11) Then Begin If rT[I]<=0 Then Begin dN[k]:=-rT[I]; End Else Begin dN[k]:=-P[I]*rT[I]; End; Inc(k); End;
For I:=0 to m-1 do For J:=0 to n-m-1 do Begin MatrixTemp[I,J]:=0; For k:=0 to m-1 do MatrixTemp[I,J]:=MatrixTemp[I,J]+BBObr[I,k]*NN[k,J]; End;
For I:=0 to m-1 do Begin dB[I]:=0; For J:=0 to n-m-1 do dB[I]:=dB[I]+MatrixTemp[I,J]*dN[J]; dB[I]:=-dB[I]; End;
k:=0;l:=0; For I:=0 to n-1 do If I in I11 Then Begin d[I]:=dB[k]; Inc(k); End Else Begin d[I]:=dN[l]; Inc(l); End;
For I:=0 to n-1 do If d[I]<0 Then Begin Lambda:=-P[I]/d[I];Break; End;
For I:=0 to n-1 do If (d[I]<0) and (-P[I]/d[I]<Lambda) Then Lambda:=-P[I]/d[I];
Lambda:=Ravnomer_Search.Search(0,Lambda,100,f,Res,0.001);
For I:=0 to n-1 do P[I]:=P[I]+Lambda*d[I];
For I:=0 to n-1 do If abs(P[I])<0.0001 Then P[I]:=0; For I:=0 to n-1 do If abs(d[I])<0.001 Then d[I]:=0; End;{While} Result:=1; End; end.
Результат работы программы. Оптимальное решение: x=(0.669,0.671). Оптимальное значение функции: 0,443.
Варианты заданий.
2.
3.
5.
6.
9.
12.
19.
22.
24.
25.
28.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 322. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 при заданных условиях:
при заданных условиях:
 1.
1. 




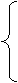


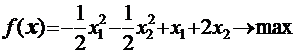


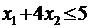
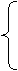 4.
4. 





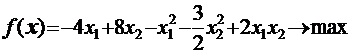



 7.
7. 

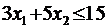





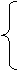 11.
11. 




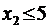
 13.
13. 

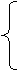 15.
15. 



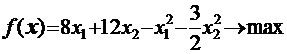









 23.
23. 


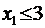

 26.
26. 









