
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретное преобразование ФурьеСтр 1 из 5Следующая ⇒ Лабораторная работа 2 ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ (4 часа)
Цель работы:изучить основные виды дискретных преобразований, используемых для цифровой обработки сигналов. Задачи работы: 1. познакомиться с дискретным преобразованием Фурье; 2. познакомиться с дискретным косинус- преобразованием; 3. закрепить полученные знания на практических примерах в пакете MATLAB.
Оглавление
Оглавление. 1 1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.. 2 1.1. Дискретные преобразования. Введение. 2 1.2. Дискретное преобразование Фурье. 3 1.3. Быстрое преобразование Фурье. 7 1.4. Дискретное косинус-преобразование. 9 1.4.1 Применение ДКП: сжатие изображений. 10 1.4.2. Двумерное ДКП.. 11 1.4.3. Квантование коэффициентов двумерного ДКП.. 12 1.4.4. Кодирование. 13 2. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ.. 15 3. КОНТРОЛЬНЫЕ ВОПРОСЫ.. 15 4. БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 16
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Дискретные преобразования. Введение
В данной лабораторной работе рассматривается преобразование дискретных данных из временной области в частотную. Зависимость напряжения от времени принято выражать через зависимость амплитуды (или фазы) от частоты, и наоборот. Эти два описания (представления) в различных областях дают дополняющую друг друга информацию об одних и тех же данных. Следовательно, в некоторых приложениях исследование графика зависимости амплитуды сигнала от частоты на предмет изменения напряжения при определенной частоте может дать больше полезной информации, чем наблюдение за формой сигнала напряжения, например, для определения первых признаков износа деталей машины. Для этого к выходным данным применяется быстрое преобразование Фурье (БПФ). Еще один пример – это использование анализатора на основе дискретного преобразования Фурье и осциллографа для проверки выхода модулятора системы связи, где пробные сигналы должны порождать амплитудные составляющие на определенных известных частотах. Внимание, которое в этих двух примерах спектрального анализа уделяется избранному и четко ограниченному набору частот, говорит о том, что выгоднее применить преобразование, при котором маловажной информацией можно пренебречь, облегчив таким образом последующую интерпретацию данных. Дискретные преобразования, в частности, дискретное косинус-преобразование, используются также для сжатия речевых и видеосигналов, что позволяет передавать их с меньшей шириной полосы. Кроме того, они применяются при обработке изображений (распознавание образов) для сокращения набора признаков. Преобразования полезны и как математическое средство ускорения вычислений в других областях обработки сигналов, таких как нахождение корреляции (используется в гидролокации для поиска объекта на большом расстоянии), или при свертке для определения взаимосвязи между системой и ее входными или выходными данными. При таких расчетах важен переход как из частотной области во временную, так и в обратном направлении. Вообще, эта тема сугубо математическая, но сегодня можно с уверенностью сказать, что в большинстве приложений дискретные преобразования стали стандартной процедурой, так что инженерам-разработчикам едва ли понадобятся глубокие математические познания или знание специальных теорем. Исключением является спектральный анализ сигналов. Здесь каждую задачу нужно рассматривать в своем контексте, при этом важно хорошо разбираться в предмете, чтобы избежать многочисленных подводных камней, связанных с необходимостью сбора достаточного количества правильных дискретных выборок, а также наложения спектров, «эффекта частокола» и просачивания спектральных составляющих. Все это будет более подробно обсуждаться в лабораторной работе по спектральному анализу.  Из всех возможных преобразований самыми известными и, пожалуй, самыми важными являются дискретное преобразование Фурье (ДПФ) и алгоритм его быстрого вычисления – быстрое преобразование Фурье (БПФ). Этому есть несколько причин: они позволяют адекватно описывать в частотных координатах все, кроме самых кратковременных (< 1 с) сигналов; усеченные по частоте Фурье-компоненты описывают данные более правдоподобно, чем любые другие степенные ряды. Отдельные компоненты представляют собой синусоиды и не искажаются при передаче через линейные системы, что позволяет использовать их как хорошие пробные сигналы. И, наконец, БПФ можно посчитать очень быстро. Еще одна причина – это то, что анализ Фурье существует с момента опубликования работы Фурье в 1822 году, и с тех пор стал широко известен, заслужил уважение и развился вместе с рядом областей своего применения. В последнее время значительное внимание уделяется вейвлетному преобразованию, поскольку оно позволяет описывать через амплитуду сигнала стохастические сигналы с переменным во времени частотным спектром. Дискретное преобразование Фурье
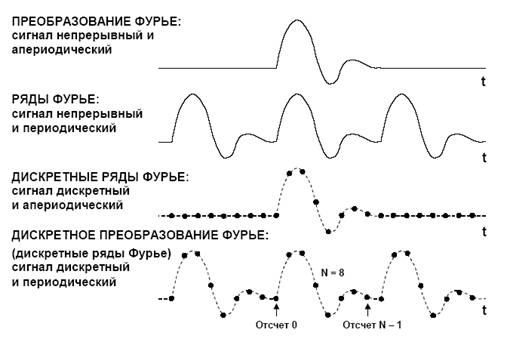
Анализ Фурье закладывает основы многих методов, применяющихся в области цифровой обработки сигналов. По сути дела, преобразование Фурье (фактически существует несколько вариантов таких преобразований) позволяет сопоставить сигналу, заданному во временной области, его эквивалентное представление в частотной области. Наоборот, если известна частотная характеристика сигнала, то обратное преобразование Фурье позволяет определить соответствующий сигнал во временной области. В дополнение к частотному анализу, эти преобразования полезны при проектировании фильтров. Частотная характеристика фильтра может быть получена посредством преобразования Фурье его импульсной реакции. И наоборот, если определена частотная характеристика сигнала, то требуемая импульсная реакция может быть получена с помощью обратного преобразования Фурье над его частотной характеристикой. Цифровые фильтры могут быть созданы на основе их импульсной реакции, поскольку коэффициенты фильтра с конечной импульсной характеристикой (КИХ) идентичны дискретной импульсной реакции фильтра. Семейство преобразований Фурье (преобразование Фурье, ряды Фурье, дискретные ряды Фурье и дискретное преобразование Фурье) представлено на рис.1. С течением времени принятые определения получили развитие (не обязательно вполне логичное) в зависимости от того, является ли сигнал непрерывно-апериодическим (continuous–aperiodic), непрерывно-периодическим (continuous–periodic), дискретно-апериодическим (sampled–aperiodic) или дискретно-периодическим (sampled–periodic). В данном контексте термин sampled означает то же самое, что discrete (дискретный) (то есть дискретные по времени выборки).
Рис.1. Семейство преобразований Фурье
Единственный член этого семейства, который имеет отношение к цифровой обработке сигналов, – это дискретное преобразование Фурье (ДПФ), которое оперирует дискретной по времени выборкой периодического сигнала во временной области. Для того, чтобы быть представленным в виде суммы синусоид, сигнал должен быть периодическим. Но в качестве набора входных данных для ДПФ доступно только конечное число отсчетов (N). Эту дилемму можно разрешить, если мысленно поместить бесконечное число одинаковых групп отсчетов до и после обрабатываемой группы, образуя, таким образом, математическую (но не реальную) периодичность, как показано на рис.1. Фундаментальное уравнение для получения N-точечного ДПФ выглядит следующим образом:
По отношению к этому уравнению следует сделать некоторые терминологические разъяснения. X(k) (прописная буква X) представляет собой частотный выход ДПФ в k-ой точке спектра, где k находится в диапазоне от 0 до N-1. N представляет собой число отсчетов при вычислении ДПФ. Значение x(n) (строчная буква x) представляет собой n-ый отсчет во временной области, где n также находится в диапазоне от 0 до N-1. В общем уравнении x(n) может быть вещественным или комплексным. Обратите внимание, что косинусоидальные и синусоидальные компоненты в уравнении могут быть выражены в полярных или прямоугольных координатах, связь между которыми определяется формулой Эйлера: e jθ = cos θ + j sin θ (2)
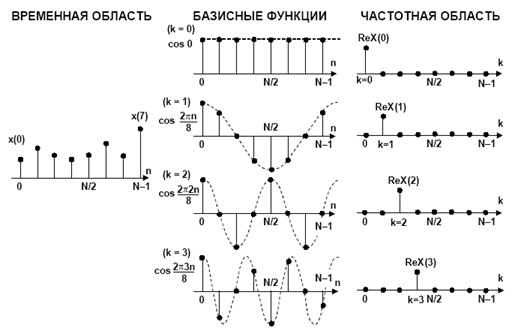
Выходной спектр ДПФ X(k) является результатом вычисления свертки между выборкой, состоящей из входных отсчетов во временной области, и набором из N пар гармонических базисных функций (косинус и синус). Концепцию хорошо иллюстрирует рис.2, на котором представлена вещественная часть первых четырех точек спектра (показаны только косинусоидальные гармонические базисные функции). Подобная же процедура используется для вычисления мнимой части спектра на основе синусоидальных функций. Первая точка X(0) является простой суммой входных отсчетов во временной области, потому что cos(0) = 1. Коэффициент масштабирования 1/N не учитывается, но должен присутствовать в конечном результате. Обратите внимание, что X(0) – это среднее значение отсчетов во временной области, или просто смещение по постоянному току. Вторая точка ReX(1) получена умножением каждого отсчета из временной области на соответствующее значение косинусоиды, имеющей один полный период на интервале N, с последующим суммированием результатов. Третья точка ReX(2) получена умножением каждого отсчета из временной области на соответствующую точку косинусоиды, которая имеет два полных периода на интервале N, с последующим суммированием результатов. Точно так же, четвертая точка ReX(3) получена умножением каждого отсчета из временной области на соответствующую точку косинусоиды с тремя полными периодами на интервале N и суммированием результатов. Этот процесс продолжается, пока не будут вычислены все N выходных отсчетов. Подобная процедура, но с использованием синусоид, применяется для вычисления мнимой части частотного спектра. Косинусоиды и синусоиды являются базисными функциями данного преобразования.
Рис.2. Свертка отсчетов во временной области с базисными функциями при ДПФ для N=8
Предположим, что входной сигнал является косинусоидальным, имеющим период N, то есть он содержит один полный период в нашей выборке. Также примем его амплитуду и фазу идентичными первой косинусоидальной базисной функции cos(2πn/8). Выходной спектр содержит одну ненулевую точку ReX(1), а все другие точки ReX(k) являются нулевыми. Предположим, что теперь входная косинусоида сдвинута вправо на 90º. Значение свертки между ней и соответствующей базисной косинусоидальной функцией равно нулю. Но алгоритм преобразования предполагает вычисление свертки с базисной функцией sin(2πn/8), необходимое для получения ImX(1). Это показывает, почему необходимо рассчитывать и вещественные, и мнимые части спектра для определения и амплитуды и фазы частотного спектра. Обратите внимание, что свертка синусоидальной/косинусоидальной функции любой частоты, отличной от частоты базовой функции, дает нулевое значение и для ReX(1), и для ImX(1). Подобная процедура применяется при вычислении обратного ДПФ для восстановления отсчетов во временной области x(n) из отсчетов в частотной области X(k). Соответствующее уравнение выглядит следующим образом:
Существует два основных типа ДПФ: вещественное ДПФ и комплексное ДПФ. Уравнения, представленные на рис.3, описывают комплексное ДПФ, где и входные, и выходные величины являются комплексными числами. Так как входные отсчеты во временной области являются вещественными и не имеют мнимой части, мнимая часть входных отсчетов всегда принимается равной нулю. Выход ДПФ X(k) содержит вещественную и мнимую компоненты, которые могут быть преобразованы в амплитуду и фазу. Вещественное ДПФ выглядит несколько проще и, в основном, является упрощением комплексного ДПФ. Большинство алгоритмов вычисления быстрого преобразования Фурье (БПФ) составлено с использованием формата комплексного ДПФ, поэтому важно понимать, как работает комплексное ДПФ и как оно соотносится с вещественным ДПФ. В частности, если известны выходные частоты вещественного ДПФ и требуется использовать обратное комплексное ДПФ для вычисления отсчетов во временной области, надо знать, как разместить выходные точки вещественного ДПФ в формате комплексного ДПФ перед выполнением обратного комплексного ДПФ.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 271. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
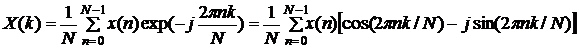 (1)
(1)
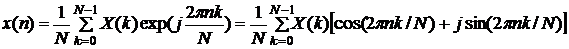 (3)
(3)