
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задание для самостоятельного выполненияЛАБОРАТОРНАЯ РАБОТА № 3 Тема: «Статистический анализ данных в MicrosoftExcel» Цель занятия:Научиться рассчитывать основные статистические характеристики в таблицах MSExcel Методические указания Экспериментальные данные определяются многими факторами. Полностью учесть все факторы и обеспечить их стабильность практически не удается, поэтому явление, определяемое этими факторами, не поддается точному предсказанию. Оно приобретает вероятностные (статистические) черты, т.е. ведет себя случайным образом. Случайным образом проявляются многие явления в природе и технике. Случайной называется величина, принимающая в опыте (или при наблюдении) определенное, но наперед неизвестное значение, зависящее от случайных причин, которые заранее не могут быть учтены. Случайные величины могут быть дискретными (прерывными) и непрерывными. Дискретной (прерывной) называется случайная величина, которая может принимать только конечное или счетное число значений. Непрерывной называется случайная величина, которая может принимать любое значение из некоторого замкнутого или открытого интервала, в т.ч. и бесконечного. Законом распределения называют правило, которое устанавливает связь между возможными значениями случайной величины и вероятностями (частотами) их появления. Наглядное представление о распределении случайных величин дает разброс песчинок, образующих кучу при высыпании (рассеивании) из некоторого точечного источника. Его проекция является параметром положения и, если куча симметрична, соответствует математическому ожиданию распределения. Разброс песчинок (параметр рассеяния), характеризуется радиусом кучи на высоте примерно 2/3. Такой параметр рассеяния соответствует так называемому стандартному (среднеквадратичному) отклонению случайных величин в распределении. Горизонтальные расстояния песчинок от проекции источника (математического ожидания) моделируют рассеяние случайной величины. Поверхность кучи (ее высоты) соответствуют частотам встречаемости случайных величин на разных расстояниях от центра. Вершина кучи, расположенная под источником, отвечает максимуму частоты. На периферии высота кучи уменьшается до нуля, что соответствует уменьшению частот больших отклонений от центра рассеяния.  Статистическая обработка совокупности данных состоит в некоторых усредняющих вычислительных процедурах, погашающих сугубо индивидуальные особенности – отклонения от общей закономерности, и подчеркивающих типичные коллективные свойства экономического объекта или явления в целом. Начальный раздел математической статистики – описательная статистика занимается характеристикой (описанием) картины случайного рассеяния по выборочной совокупности данных. В соответствии с законом ее распределения решаются вопросы выбора и вычислений надлежащих показателей. Задание. 1. Организуйте в Excel представленную ниже одномерную выборку (для получения результатов описательной статистики одномерную выборку необходимо поместить в одном столбце).
2. Выясните, однородна ли представленная выборка. Наглядное представление об однородности выборки дает ее графическое отображение столбчатой диаграммой, которая называетсягистограммой. Ее горизонтальная ось отвечает значениям случайной величины, откладываемым поинтервально (диапазон колебаний – размах делится на интервалы). Каждому интервалу соответствует вертикальный столбик с высотой, равной частоте попадания случайной величины в этот интервал.
- Обратитесь вкладка Данные/Анализ данных/Гистограмма. Сделайте нужные установки (укажите лишь диапазон входных данных (случайных величин) и диапазон вывода результата) и выполните команду. - Рассмотрите результат, представленный на рисунке ниже. Карманы – это и есть интервалы. - Постройте гистограмму, показывающую частоту попадания случайных значений в вычисленные интервалы. Результаты графических построений позволяют визуально оценить однородность совокупности. Поскольку гистограмма имеет один максимум с монотонными уменьшениями частот (спусками), т.е. примерно отвечает вертикальному разрезу через кучу песчинок, то совокупность можно считать близкой к однородной. 3. Выведите на экран параметры распределения. Параметры распределения, т.е. описательная статистика, имеют смысл только для однородной статистической совокупности. Убедившись в однородности совокупности, можно определять ее характеристики. Для этого используются либо модуль «Анализ данных», либо встроенные функции. На вкладкеДанные/Анализ данных/Описательная статистика сделайте необходимые установки и выполните автоматический анализ. Рассмотрите результаты. Медиана случайной величины – такое ее значение, которое делит площадь гистограммы пополам. Мода распределения случайной величины – такое ее значение (такой интервал), при котором гистограмма достигает максимума. Стандартное отклонение – среднеквадратичное отклонение вариант от среднего арифметического. Дисперсия выборки – математическое ожидание квадрата отклонения случайной величины от своего математического ожидания (квадрат стандартного отклонения). Эксцесс характеризует островершинность кривой. У нормального распределения он равен 0 и может быть использован для выяснения отклонения распределения от нормального. Асимметричность характеризует симметрию распределения. У нормального распределения она равна 0 и может быть использована для выяснения отклонения распределения от нормального. Интервал– это размах, т.е. разность между указываемыми ниже максимумом и минимумом значений вариант. Сумма – сумма значений вариант. Счет – количество вариант. Задание для самостоятельного выполнения Составить дискретный или интервальный ряд распределения, изобразить его графически, определить важнейшие характеристики распределения: среднее арифметическое, дисперсию, среднее отклонение, ошибку средней, моду, медиану и коэффициент вариации для данных представленных в таблице 1. Таблица 1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 254. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
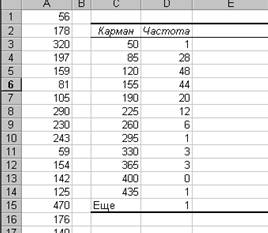 Для нормального распределения интервалы берутся равными. Сложнее вопрос числа интервалов. Excel располагает возможностями автоматического разрешения этих проблем.
Для нормального распределения интервалы берутся равными. Сложнее вопрос числа интервалов. Excel располагает возможностями автоматического разрешения этих проблем.