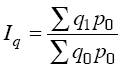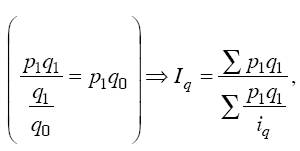Построение сводных территориальных индексов

При построении территориальных индексов, т. е. при сравнении показателей в пространстве (межрайонные, сравнение между разными предприятиями и др.), возникают вопросы о выборе базы сравнения и района (объекта), на уровне которого следует зафиксировать веса индекса. В каждом конкретном случае эти вопросы нужно решать исходя из задач исследования. Выбор базы сравнения зависит, в частности, от того, будут ли сравнения двусторонними (например, сравнение показателей двух соседних территориальных единиц) или многосторонними (сравнение показателей нескольких территорий, объектов).

При двусторонних сравнениях каждая территория или объект с одинаковым основанием может быть принят как в качестве сравниваемого, так и в качестве базы сравнения. В связи с этим возникает вопрос о фиксировании весов сводного индекса на уровне того или иного района (объекта). Пусть, например, нужно определить, в какой из двух областей и насколько процентов ниже себестоимость единицы продукции и больше объем ее производства.

Если сравнивать область А с областью Б, достаточно обоснованный и простой путь состоит в том, чтобы зафиксировать в индексе себестоимости в качестве весов объемы продукции в целом по обеим территориям (Q = QA + QБ), тогда получим: Iz =?zQ/?zQ.

При многосторонних сравнениях, например при сравнениях качественных показателей по нескольким областям, нужно, соответственно, расширить и границы территории, на уровне которой фиксируются веса.

В сводных территориальных индексах объемных показателей в качестве весов могут быть приняты средние уровни соответствующих качественных показателей, вычисленные в целом по сравниваемым территориям. Так, в нашем примере

Средние индексы

В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса, т. е. он может быть преобразован в средний арифметический и средний гармонический индексы.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне объяснима: ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и, конечно, его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.

Например, известен индивидуальный индекс физического объема iq = q1/q0 и стоимость продукции каждого вида в базисном периоде (q0p0). Исходной базой построения среднего из индивидуальных индексов служит сводный индекс физического объема:

(агрегатная форма индекса Ласпейреса).

Из имеющихся данных непосредственно суммированием можно получить только знаменатель формулы. Числитель же может быть получен перемножением стоимости отдельного вида продукции базисного периода на индивидуальный индекс:

Тогда формула сводного индекса примет вид:

т. е. получим средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.

Допустим, что в наличии имеется информация о динамике объема выпуска каждого вида продукции (г) и стоимости каждого вида продукции в отчетном периоде (p1q1). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

Числитель формулы можно получить суммированием величин q1P1, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением: p1q1/iq , тогда:

таким образом, получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах, т. е. когда агрегатный индекс построен по сравнимому кругу единиц (агрегатные индексы качественных показателей и агрегатные индексы объемных показателей при условии сравнимого ассортимента).

ЛЕКЦИЯ № 8