
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дизъюнктивные нормальные формы
Определение. Элементарной конъюнкцией называется конъюнкция литералов (переменных или их отрицаний), взятых не более чем по одному разу.
Например, конъюнкции Следующие конъюнкции:
Определение.Элементарная конъюнкция булевой функции Определение. Дизъюнкция любого конечного множества элементарных конъюнкций булевой функции F называется дизъюнктивной нормальной формой (ДНФ) функции F. Число элементарных конъюнкций (слагаемых, термов), составляющих ДНФ, называется длиной ДНФ.
Например, ДНФ
Для произвольной булевой функции F существует, вообще говоря, много различных реализующих ее ДНФ, отличающихся друг от друга длиной, числом вхождений литералов и т.д. Определение. Две (или несколько) ДНФ, реализующих одну и ту же булеву функцию F , называются эквивалентными (или равносильными).
Например, для функции
Определение. ДНФ булевой функции F, состоящая только из полных элементарных конъюнкций, называется совершеннойДНФ(СДНФ). 
Например, (1) - СДНФ функции F. Отметим, что СДНФ является единственной (с точностью перестановки слагаемых) для конкретной булевой функции F .
Любую булеву функцию F, заданную формулой, можно с помощью основных равносильностей преобразовать к ДНФ, а затем к СДНФ. Пример.Привести к виду СДНФ булеву функцию F=
Решение.С помощью основных равносильностей преобразуем к ДНФ:
Применяя закон склеивания (в обратном порядке:
Так как Составим таблицу истинности для булевой функции F=
Таблица истинности СДНФ
В общем случае также можно вывести закономерности построения СДНФ по таблице истинности булевой функции, что является очень удобным.
СДНФ состоит из дизъюнкций полных элементарных конъюнкций наборов переменных Пример. По таблице истинности составить СДНФ
Решение: СДНФ:
Пример. Для булевой функции, заданной в виде ДНФ Решение: Применяя закон склеивания (в обратном порядке:
Так как
Таблица истинности СДНФ
Минимизация ДНФ Определение. Элементарная конъюнкция u называется импликантой булевой функции F , если
Например, элементарная конъюнкция Определение. Если никакая собственная часть
Например,
Определение. Дизъюнкция всех простых импликант булевой функции F называется сокращенной ДНФ (СкДНФ)функции F .
Например, Определение.ДНФ булевой функции F , содержащая наименьшее число слагаемых среди всех ДНФ, реализующих функцию F , называется кратчайшей ДНФ (КрДНФ).
Например,
Вообще говоря, для заданной булевой функции F существует несколько различных по числу вхождений литералов КрДНФ.
Определение.ДНФ булевой функции F , содержавшая наименьшее число вхождений литералов среди всех ДНФ, реализующих функцию F , называется минимальной ДНФ (МДНФ).
Отметим, что для заданной булевой функции F существует, вообще говоря, несколько МДНФ, отличающихся друг от друга числом слагаемых.
Более того, МДНФ не всегда совпадает с КрДНФ булевой функции n переменных F . Хотя для начальных значений n ( n = 2 или n = 3 ) МДНФ всегда совпадает с КрДНФ). Например, Задача минимизации булевой функции
Причем, если раньше (при синтезе контактных схем) основное внимание уделялось построению МДНФ, то в настоящее время (при синтезе логических схем на элементах И,ИЛИ,НЕ, И-НЕ и др.) требуется построение КрДНФ.
Также отметим, что задача минимизации булевых функций n переменных F в классе ДНФ является чрезвычайно громоздкой и ее трудоемкость с ростом n возрастает по экспоненциальному закону.
К настоящему времени разработано около 200 различных методов минимизации булевых функций в классе ДНФ, наиболее известными среди которых являются метод Квайна - Мак-класки, метод Блейк-Порецкого, метод Нельсона, метод неопределенных коэффициентов и др. Пример. Составить по таблице истинности СДНФ булевой функции Решение
СДНФ будет иметь вид Минимизируем ее, применяя законы склеивания. Подчеркнем конъюнкции, которые можно склеить. Очевидно, что это можно сделать различными способами, например:
Выберем один из возможных вариантов склеивания, например:
Замечание.При минимизации ДНФ достаточно часто (но не всегда!) удается получить лучшие результаты, если «нарастить» данную ДНФ, используя свойство идемпотентности дизъюнкции:
Например, в рассматриваемом примере пятую, последнюю конъюнкцию
Пример. Составить СДНФ булевой функции, заданной вектором значений таблицы истинности w(F)=(10010010), и минимизировать ее, применяя законы склеивания. Решение.Так как вектор значений заданной булевой функции имеет 8=23 разрядов, следовательно, булевой функции соответствует следующая таблица истинности:
СДНФ будет иметь вид:
К сожалению, минимизировать ее, применяя законы склеивания, невозможно. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 226. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  , 1 являются элементарными. Причем первая элементарная конъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0.
, 1 являются элементарными. Причем первая элементарная конъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0. ,
,  ,
,  ,
,  , 0 не являются элементарными.
, 0 не являются элементарными. , содержащая n литералов, называется полной (или минтермом).
, содержащая n литералов, называется полной (или минтермом). имеет длину, равную 3.
имеет длину, равную 3. , заданной булевым вектором w(F)=(00100111), существуют следующие эквивалентные ДНФ:
, заданной булевым вектором w(F)=(00100111), существуют следующие эквивалентные ДНФ: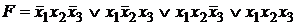 , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4) . (5)
. (5) .
. =
=  =
=  =
= =
=  - ДНФ.
- ДНФ. ), дополняем конъюнкции
), дополняем конъюнкции  ,
,  до полных элементарных конъюнкций:
до полных элементарных конъюнкций: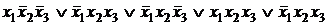 .
.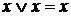 , то после сокращения одинаковых конъюнкций, получаем СДНФ: F=
, то после сокращения одинаковых конъюнкций, получаем СДНФ: F=  .
.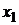




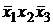



 , на которых функция принимает значение 1. Переменные берутся без отрицания, если им соответствует в таблице истинности 1, с отрицанием, если 0.
, на которых функция принимает значение 1. Переменные берутся без отрицания, если им соответствует в таблице истинности 1, с отрицанием, если 0. .
. , составить СДНФ и выполнить проверку по таблице истинности.
, составить СДНФ и выполнить проверку по таблице истинности.
 .
. .
.




 .
.  импликанты u (т.е.
импликанты u (т.е.  ) булевой функции F не является импликантой F, то u называется простойимпликантой (т.е. если удаление из u хотя бы одного литерала нарушает условие
) булевой функции F не является импликантой F, то u называется простойимпликантой (т.е. если удаление из u хотя бы одного литерала нарушает условие  (собственная часть импликанты
(собственная часть импликанты  и минимизировать ее, применяя законы склеивания.
и минимизировать ее, применяя законы склеивания.
 .
. ,
, ,
, ,
, .
.

 .
. можно было бы склеить со второй конъюнкцией
можно было бы склеить со второй конъюнкцией  . Добавив вторую конъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации ДНФ более короткое ее представление:
. Добавив вторую конъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации ДНФ более короткое ее представление:

 .
. .
.