Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Физическое представление цифровых сигналовСтр 1 из 5Следующая ⇒ До сих пор под цифровым сигналом понимался абстрактный сигнал, состоящий их логических нулей и единиц, называемых битами. Битовый поток является носителем информации, которая является нематериальной вещью. Для передачи этой информации по реальному каналу связи необходимо битовый поток представить в виде реальных сигналов, например импульсов напряжения или тока. Этими сигналами производится модуляция несущей частоты для передачи по радиоканалу. И здесь немаловажное значение приобретает конкретная форма представления цифрового сигнала, поскольку в реальном канале связи существуют жесткие ограничения на параметры этого сигнала и в первую очередь — на его ширину спектра.
Рис. 3.1. Прямоугольные импульсы (а) и спектр при их периодической последовательности (б) Самой простой формой цифрового сигнала является его представление в виде прямоугольного импульса длительностью τ, как показано на рис. 3.1, а. Спектр этого импульса показан на рис. 3.1, б пунктирной линией. При периодическойпоследовательности импульсов он превращается в линейчатый. Реальные цифровые сигналы не являются строго периодическими функциями, но близки к ним. Отметим, что ширина спектра равна бесконечности и не может быть реализована. На практике ширину спектра ограничивают. Для достаточно хорошего воспроизведения формы импульсов можно взять 10... 15 гармоник сигнала, т.е. ограничить ширину спектра до Δf= (10...15)/Тb, где Т— период следования импульсов(тактовый интервал Тb). Важным параметром передачи цифрового потока является удельная скорость передачи символов, которая определяется как отношение количества передаваемых символов RSза единицу времени к ширине полосы канала: 
Rn=Rs/Δf,(бит/с)/Гц.
Рис. 3.2. Межсимвольная интерференция при ограничении ширины спектра сигнала.
Отсюда следует, что использование прямоугольных импульсов для представления цифровых символов явно не выгодно. В тоже время, существуют такие сигналы, которые обладают ограниченными спектрами и не имеют межсимвольной интерференции. К таким сигналам относитсясигнал вида sinx/x, временная зависимость которого показана на рис. 3.3. Действительно, для таких импульсов, если брать отсчеты точно в моменты Т, 2Т, 3Т и т.д., влияние соседних импульсов будет отсутствовать. Рассматриваемый сигнал теоретически бесконечен, а его спектр ограничен полосой 1/2Т. Рассчитаем по формуле (3.1) удельную скорость передачи символов
Таким образом, для передачи цифрового потока со скоростью 4 Мбит/с потребуется полоса 2 МГц. Однако на самом деле реализовать импульсы в форме sinx/xневозможно по двум причинам: во-первых, эти импульсы имеют бесконечную длительность; во-вторых, отсчеты необходимо брать исключительно точно в моменты Т, 2Т, 3Т, ..., в противном случае возникает значительная межсимвольная интерференция. Удельную скорость RN= 2 (бит/с)/Гц, как было отмечено выше, можно рассматривать как теоретический предел скорости передачи физических символов.
Поэтому на практике используют некоторый компромиссный вариант между прямоугольным импульсом и импульсом типа sinx/x. Его можно получить, пропуская импульс в виде δ-функции через фильтр со сглаженными границами полосы пропускания. На рис. 5.4. показан пример АЧХ - H(f)такого фильтра. На рисунке fN=1/2Т — частота Найквиста определяет частоту среза идеального фильтра, на выходе которого можно было бы получить импульс типа sinx/x. Однако реализовать такой фильтр физически невозможно. АЧХ реального фильтра характеризуется коэффициентом сглаживанияα. В результате сглаживания происходит снижение удельной скорости передачи до 30-50% от барьера Найквиста. В таком случае информационный поток со скоростью 4 Мбит/с можно передать в полосе 4-6 МГц. Но и этот объем информации нельзя признать удовлетворяющим современные потребностям. Виды модуляции Чтобы осуществить эффективную передачу сигналов в какой-либо среде, необходимо перенести спектр этих сигналов из низкочастотной области в область достаточно высоких частот. Данная процедура получила в радиотехнике название модуляции. Сущность модуляции заключается в следующем. Формируется некоторое колебание (чаще всего гармоническое), называемое несущим колебанием или просто несущей, и какой-либо из параметров этого колебания изменяется во времени пропорционально исходному сигналу. Исходный сигнал называют модулирующим, а результирующее колебание с изменяющимися во времени параметрами — модулированным сигналом. Обратный процесс — выделение модулирующего сигнала из модулированного колебания — называется демодуляцией. Имеется гармонический сигнал общего вида: U(t) = A cos(ω0t+ φ0). У данного сигнала есть три параметра: -амплитуда А; - частота ω0 ; - начальная фаза φ0. Каждый из них можно связать с модулирующим сигналом, получив, таким образом, три основных вида модуляции: амплитудную, частотную и фазовую. Частотная и фазовая модуляция очень тесно взаимосвязаны, поскольку обе они влияют на аргумент функции cos. Поэтому эти два вида модуляции имеют общее название — угловая модуляция. Амплитудная модуляция При амплитудной модуляции(АМ) амплитуда несущего колебания изменяется в соответствии с изменением мгновенного значения модулирующего сигнала. На рис.3.5 представлены формы модулирующего, модулируемого и амплитудно-модулированных сигналов. Для простоты анализа в качестве модулирующего первичного сигнала взято гармоническое колебание низкой частоты Ω. В качестве модулируемого колебания взято высокочастотное колебание несущей частоты ω. Амплитудно-модулированное колебание представляет собой высокочастотное колебание, амплитуда которого изменяется по закону изменения напряжения низкой частоты. Степень воздействия модулирующего колебания на колебание несущей частоты оценивается коэффициентом (глубиной) амплитудной модуляции, который определяется выражением
где
Амплитудно-модулированное колебание является сложным и не является простой суммой колебаний высокой и низкой частот. Покажем это. Пусть колебания высокой и низкой частот являются гармоническими и определяются выражениями: uω=Uωsinωt uΩ=UΩcosΩt
Рис. 3.5. Принцип амплитудной модуляции
В процессе модуляции амплитуда напряжения ВЧ сигнала изменяется по закону низкочастотного сигнала: Uω= Тогда мгновенное значение модулированного напряжения можно записать в виде um= Применив тригонометрическую формулу sin ωt получим:
Полученный результат показывает, что АМ колебание представляет собой сумму трех высокочастотных колебаний, имеющих частоты ω , Частоты
Рис.3.6. Спектр АМ сигнала
Частотная модуляция При частотной модуляции(ЧМ) амплитуда модулированного несущего колебания остается неизменной, а меняется только его частота в соответствии с изменением амплитуды первичного сигнала. На рис. 3.7 показаны формы исходного (модулирующего) и частотно-модулированного сигналов. Максимальное отклонение частоты от среднего значения несущей называется девиацией частоты: Δωчм=ωmax-ω0= ω0-ωmin или Δfчм=fmax-f0= f0- fmin Отношение Δωчм/Ω= Δfчм/F=mf называется индексом частотной модуляции. Здесь ω, (F) – частота первичного сигнала. Полагая, что начальная фаза равна нулю (при t = 0), можно записать уравнение сигнала при частотной модуляции: Uчм(t)=U0cos(ω0 t + mf sinΩt)
Рис. 3.7. Принцип частотной модуляции
Также как АМ колебание, частотно-модулированное колебание является сложным. Разложение ЧМ сигнала на гармонические составляющие требует достаточно сложных математических преобразований с использованием функции Бесселя. Выполнение этих преобразований показывает, что спектр колебания при частотной модуляции состоит из колебаний с частотами w0 (f0) и бесконечного числа боковых частот, расположенных попарно симметрично относительно несущей частоты w0 и отличающихся от последней на nΩ, где n - любое целое число. Амплитуды боковых составляющих определяются выражением Un=U0Jn(mj) где U0 – амплитуда ВЧ колебания; Jn(mj) – функция Бесселя n-го порядка от аргумента mj . Пример спектра ЧМ сигнала показан на рис. 3.8.
Рис. 3.8. Спектр ЧМ сигнала
По величине индекса частотной модуляции различают: – узкополосную ЧМ, когда mf< 1, т.е. Δfчм < F; – широкополосную ЧМ, когда mf >1, т.е. Δfчм > F;. Теоретически спектр ЧМ колебаний бесконечно широк. Практически, начиная с некоторых частот, амплитуды гармоник столь малы, что ими можно пренебречь. На этом основании ширина спектра ЧМ колебаний определяется как диапазон частот, расположенный симметрично относительно несущей, за пределами которого нет гармоник с амплитудами, превосходящими 0,01 U0 . Приближенно ширина спектра определяется формулой
Например, при девиации частоты Δfчм = 5 кГц и наивысшей частоте спектра звукового сигнала F = 3,4 кГц, ширина спектра ЧМ сигнала составит ΔFc≈2(5+3,4)=16,8 кГц. При большом индексе частотной модуляции, когда mf >>1, формула (3.3) принимает вид ΔFc ≈2mfF=2Δfчм, т. е. ширина спектра практически равна удвоенной величине девиации частоты и не зависит от от частоты модуляции. При малом индексе частотной модуляции mf << 1ширина спектра будет равна ΔFc =2F , т. е. составит такую же величину, как и при амплитудной
Фазовая модуляция При фазовой модуляции (ФМ) передаваемое сообщение изменяет значение фазы несущей. Таким образом, фаза «несущей» изменяется пропорционально мгновенным значениям модулируемого сигнала(см. рисунок 3.9) j=Dj× sinWt (3.4) При увеличении модулируемого сигнала частоты W возникает опережение по фазе Dj×sinWt, гдеDj – максимальный сдвиг по фазе или девиация фазы.
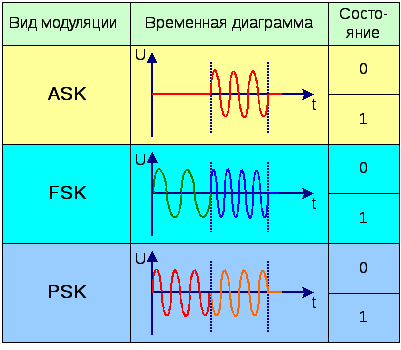
Dj – девиация фазы Рисунок 3.9 Фазовая модуляция Значение ФМ – колебания: U фмс(t ) = U0 cos (w0t +mф sinW t) (3.5) аналогично Uчмс с той лишь разницей, что при ФМ индекс модуляции: mф=Dj (3.6) При ФМ изменяется не только фаза, но и мгновенная частота «несущей». Точно также при ЧМ изменяется и фаза несущей. Таким образом, ФМ и ЧМ в какой- то мере аналогичны и отличаются друг от друга методами осуществления.ФМ и ЧМ связаны, поэтому они могут быть объединены в понятие как угловая модуляция: Dw=W×Dj (3.7) – девиация угловой частоты. Полоса частот при ФМ определяется выражением: D Fф =2 F( mф+1) (3.6) Так как при ЧМ индекс модуляции согласноmf= Δωчм/Ωуменьшается с увеличением частоты сигнала, а при ФМ он не зависит от неё (mф=Dj), то ширина полосы частот при ФМ оказывается больше, чем при ЧМ. При mф<<1спектр частот ЧМ и ФМ состоит из несущей и двух боковых полос как при АМ. При mф>> 1 спектр частот ФМ схож со спектром при ЧМ с той лишь разницей, что при ФМ боковые частоты не зависят от частоты сигнала, тогда как при ЧМ амплитуда этих частот уменьшается с увеличением частоты сигнала. Цифровые способы модуляции Свойства цифрового сигнала не позволяют передавать такой сигнал по каналу связи непосредственно, то есть «в первичной полосе частот» из-за слишком высокой скорости передачи, оцениваемой в сотни мегабит в секунду. Кроме того, существующие сети, как правило, построены по принципу частотного уплотнения. Поэтому сигнал, предназначенный для передачи по таким сетям, должен быть точно ориентирован в принятой системе организации частотных каналов. Следует также иметь в виду, что передаваемый сигнал должен быть энергетически сосредоточен в определенной ограниченной области спектра. Как правило, несущей (модулируемой) частотой является гармонический сигнал. Изменяемыми параметрами, как мы уже отмечали, в таком случае могут быть его амплитуда, частота и фаза. Если модулирующий сигнал имеет цифровую природу и изменяется дискретно, принимая фиксированные значения, то понятие «модуляция» иногда заменяется понятием «манипуляция». Передаваемый сигнал, таким образом, в результате модуляции можно представить в следующей форме U(t) = (Амплитуда)cos[2π(Частота)t + (Фаза)] Использование для передачи цифровых сигналов различных видов модуляции позволяет одновременно увеличить количество передаваемой информации в единицу времени, сократить используемую полосу частот и повысить помехоустойчивость систем. В передаче цифровых сигналов может применяться амплитудная модуляция (AM), в иностранной литературе применительно к цифровому сигналу называемая ASK (Amplitude Shift Keying); частотная модуляция (ЧМ), ее обозначают также FSK (Frequency Shift Keying), и фазовая модуляция (ФМ), англоязычное обозначение PSK (Phase Shift Keying). На рис. 3.10 иллюстрируется принцип работы каждого из применяемых видов модуляции для двухпозиционного модулирующего сигнала, то есть когда каждое состояние сигнала передает один бит информации. На рис. 3.10 также показаны графики, поясняющие изменение сигнала во времени.
Рис. 3.10 — Виды модуляции при двухпозиционном модулирующем сигнале Демодуляция рассмотренных сигналов достаточно проста в техническом отношении, и для ее осуществления известно много способов. Качество того или иного способа модуляции при передаче цифровых сигналов оценивается обычно по следующим критериям:
Эффективность использования частотного спектра увеличивается с увеличением числа состояний, которые может принимать сигнал при передаче одного символа. Если модулирующим сигналом является сигнал, в котором каждый символ передается не двумя, а большим количеством возможных его значений, то количество информации, передаваемое с каждым символом, возрастает. Такие значения обычно выбираются равными 4, 16, 32, 64, 128 и т.д., то есть как ряд 2n, где n — число возможных состояний передаваемого или модулирующего сигнала во время передачи одного символа. Чем выше количество информации, переносимое одним символом, тем выше число возможных состояний, которое может принять изменяемый в процессе модуляции параметр модулируемого сигнала, и соответственно тем выше эффективность использования частотного спектра. Однако, чем большее число состояний может принимать модулирующий сигнал, тем меньше существует отличий в параметрах этих состояний, а значит, демодуляция такого сигнала в условиях помех может стать затруднительной. Поэтому эффективность использования частотного спектра обычно связана с возможно достижимым отношением сигнал/помеха, и при выборе этих параметров необходим компромисс. Сигнальные созвездия 3.4.1.1. Полярные диаграммы Удобным средством анализа характеристик модулированных сигналов является отображение их с помощью полярных и квадратурных диаграмм в виде сигнальных созвездий. Наиболее простой способ отображения амплитудно-фазовых соотношений модулированного сигнала — это полярная диаграмма. При построении полярной диаграммы несущая является опорным элементом, относительно которого отсчитывается угол фазового сдвига и изменение уровня модулированного сигнала. Модуль радиус-вектора, исходящего из центра окружности (начала координат), характеризует относительный уровень элементарного сигнала, а угол наклона между радиус-вектором и некоторым начальным радиусом — текущий фазовый сдвиг. Математически это можно выразить стандартной записью модулированного сигнала u(t) = Асоs(ωt+θ) = АRе{еj(ωt+θ)} = АRе{еjωtеjθ}. (3.8) Отображение сигнала u(t) на полярной диаграмме соответствует его «замораживанию» во времени, когда фиксируются только амплитуда сигнала А и его начальный фазовый сдвиг θ. Экспоненциальная форма записи сигнала позволяет выделить сомножители, характеризующие частоту несущей еjωt и ее фазу еjθ. При построении полярной диаграммы частотный сомножитель исключается, а остается только фазовый. Примеры полярных диаграмм, показывающих характерные изменения значащих параметров для амплитудной, фазовой и амплитудно-фазовой модуляций, показаны на рис. 3.11. При чистой амплитудной модуляции переход между значащими позициями (М1 и М2) осуществляется по прямой линии (кратчайшему расстоянию) между ними. При чистой фазовой модуляции — по дуге окружности. Соответственно изменяются либо уровень, либо фазовый сдвиг модулированного сигнала. При возникновении паразитной модуляции иного свойства переход будет характеризоваться некоторой кривой линией. При совместной амплитудно-фазовой модуляции переход осуществляется по прямой линии, связывающей точки с различными фазовыми углами.
Рис. 3.11 — Полярные диаграммы для амплитудной (а), фазовой (б) и амплитудно-фазовой (в) модуляций Квадратурные диаграммы Модуляторы для цифровых систем передачи строятся, как правило, по квадратурной схеме. В таком модуляторе выходной сигнал образуется суммированием двух различных модулированных сигналов, несущие которых имеют между собой фазовый сдвиг 90°. Входы двух модулирующих сигналов квадратурного модулятора обозначаются I и Q: I (синфазный) относится к каналу, в котором начальный фазовый сдвиг несущей принимается равным 0°; Q — к каналу, несущая в котором сдвинута на 90°. Для адекватного отображения пространства сигналов на выходе квадратурного модулятора полярные диаграммы преобразуют в прямоугольную систему координат, в которой по горизонтальной оси I откладывают уровень сигнала в синфазном канале, а по вертикальной оси Q — уровень сигнала в квадратурном канале. Все остальные построения соответствуют полярной диаграмме с учетом того, что ось I символизирует нулевой фазовый сдвиг, а ось Q — сдвиг на 90°. Проекции вектора сигнала на оси I и Q‚ рассматривают как его квадратурные компоненты. Рис. 3.12 поясняет переход от полярной диаграммы к квадратурной.
Рис.3.12 — К пояснению преобразования полярной диаграммы в квадратурную Полные квадратурные диаграммы для 4-PSK и 8-PSK показаны на рис. 3.13.
Рис.3.13 — Полные квадратурные диаграммы для модуляций 4-PSK (а) и 8-PSK (б) Для упрощения рисунка квадратурной диаграммы, особенно при отображении сигналов современных многопозиционных видов модуляции, обычно изображают только конечные точки векторов, исходящих из начала координат, а сами векторы, как правило, опускают. Часто опускают и сами оси I и Q, подразумевая, что они проходят через центр симметрии фигуры. Полное множество модулированных сигналов, изображенных на квадратурной диаграмме в виде точек, называют сигнальным созвездием, а сами сигналы — точками созвездия. Форма сигнального созвездия соответствует виду модуляции, а расстояния между точками созвездия характеризуют помехоустойчивость при приеме сигнала. Если требуется пометить точки созвездия, рядом с ними размещают значения битов модулирующих сигналов, которые порождают данный модулированный сигнал с конкретными значениями фазы и амплитуды. В качестве примера на рис.3.14 показаны несколько простых созвездий: одномерных для амплитудной модуляции (АМ) и двумерныхдля фазовой модуляции (PSK), геометрическим местом точек которых являются соответственно прямая и окружность.
Рис.3.14 — Сигнальные созвездия для амплитудной (а) и фазовой (б) модуляций Здесь следует заметить, что показанные созвездия АМ получаются при использовании в качестве модулирующего сигнала биполярных импульсов, значащие уровни которых симметричны относительно нулевого уровня. При модуляции отрицательными импульсами одновременно изменяется на противоположную и фаза сигнала. Поэтому такая АМ может рассматриваться и как разновидность PSK. При классической АМ с пассивной паузой, когда состоянию 1 соответствует некоторый уровень несущей, а состоянию 0 — отсутствие несущей, созвездие будет иметь несимметричный характер: точка 0 будет расположена в центре координат, а точка 1 — в области положительных значений оси I. При однополярном многоуровневом модулирующем сигнале созвездие АМ представляется рядом точек на одной из полуосей I. При классической фазовой модуляции изменению подлежит только фаза сигнала при неизменной его амплитуде. Поэтому в зависимости от кратности модуляции созвездие PSK представлено соответствующим числом точек, расположенных на окружности. Двоичная фазовая модуляция ничем не отличается от двоичной АМ с биполярным модулирующим сигналом и имеет такое же одномерное созвездие. Диаграммы состояний Полярным и квадратурным диаграммам иногда придают свойства диаграммы состояний, показывая стрелками допустимые пути перехода между точками созвездия. Центр квадратурной диаграммы соответствует нулевому уровню несущей. Поэтому, если переход из одной точки созвездия в другую происходит через начало координат, то это адекватно сильному изменению огибающей модулированной несущей с переходом ее через ноль. Большие изменения уровня несущей повышают требования к линейности тракта, иначе в спектре сигнала могут возникать дополнительные гармонические составляющие, приводящие к комбинационным искажениям и расширению спектра передаваемого сигнала. Сильные вариации уровня возникают при одновременной инверсии значений битов в каналах I и Q. Если инверсия битов возникает только в одном из квадратурных каналов, то уровень несущей изменяется мало, во всяком случае исключаются переходы через ноль. Для получения эффекта ограниченного изменения уровня несущей применяют специальные методы, связанные с преобразованием структуры и формы модулирующих сигналов: относительное кодирование, сдвиг во времени (офсет) сигналов в каналах I и Q, найквистовскую фильтрацию. |
|||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 432. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 Для рассмотренного выше примера RS= 1/Т, а удельная скорость передачи составляет 0,07…0,1 (бит/с)/Гц. Например, если потребуется передать цифровой поток со скоростью 4 Мбит/с, то требуемая полоса канала составит 40…60 МГц. Такая полоса является чрезмерно большой. Искусственное сокращение ширины спектра импульсовприводит к искажению их формы и увеличению длительности переходных процессов, возникающих после прохождения цепи, ограничивающей спектр сигнала. Это показано на рис. 3.2.
Для рассмотренного выше примера RS= 1/Т, а удельная скорость передачи составляет 0,07…0,1 (бит/с)/Гц. Например, если потребуется передать цифровой поток со скоростью 4 Мбит/с, то требуемая полоса канала составит 40…60 МГц. Такая полоса является чрезмерно большой. Искусственное сокращение ширины спектра импульсовприводит к искажению их формы и увеличению длительности переходных процессов, возникающих после прохождения цепи, ограничивающей спектр сигнала. Это показано на рис. 3.2.

 Рис. 3.4. АЧХ идеального и реального фильтров: fN= 1/2Т — частота Найквиста, а— коэффициент сглаживания
Рис. 3.4. АЧХ идеального и реального фильтров: fN= 1/2Т — частота Найквиста, а— коэффициент сглаживания

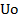 – амплитуда несущего высокочастотного колебания;
– амплитуда несущего высокочастотного колебания; –превышение амплитуды АМ колебания над
–превышение амплитуды АМ колебания над 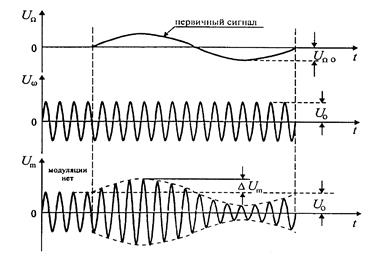
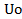 +
+ 
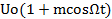 sinωt
sinωt
 +1/2
+1/2  (3.2)
(3.2)
 и
и  , и не содержит в себе низкой частоты
, и не содержит в себе низкой частоты  полезного сигнала.
полезного сигнала.