
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоретические сведенияКафедра общей и технической физики Лабораторная работа 1 Анализ магнитных примесей методом ЭПР
Автор: Парфенова И.И.
Санкт-Петербург 2008 Цель работы- определение g-фактора электрона с помощью электронного парамагнитного резонатора.
Основные теоретические сведения Электронный парамагнитный резонанс (ЭПР) связан с одним из важных свойств электронов - с их способностью ориентироваться определенным образом во внешнем магнитном поле. Электронам присуще особого рода внутреннее движение, с которым связан момент импульса, который называется спином. Этому внутреннему моменту импульса соответствует постоянный магнитный момент, направленный противоположно спину. В отсутствие магнитного поля направление (ориентация) магнитного момента свободного электрона в пространстве может быть любым; энергия такого электрона не зависит от ориентации его магнитного момента. Во внешнем магнитном поле, в соответствии с законами квантовой механики, ориентация магнитного момента электрона не может быть произвольной: магнитный момент может быть направлен либо по направлению магнитного поля, либо противоположно ему (рис.1а). Соответственно энергия электрона во внешнем магнитном поле зависит от индукции этого поля В и от ориентации магнитного момента электрона относительно поля, т.е. может принимать лишь два значения E1 и E2.
Рис. 1. Пространственное квантование спинов 
Рис. 2. Поглощение энергии переменного электромагнитного поля свободным электроном в постоянном магнитном поле B. Магнитные свойства электрона, входящего в состав атома или молекулы, сложнее. В этом случае электрон может двигаться лишь по вполне определенным орбитам, каждой из которых соответствует свой энергетический уровень. Может случиться так, что некоторые уровни будут иметь одинаковую энергию, это называется вырождением. Число возможных состояний с данной энергией E называется степенью вырождения. С орбитальным движением электрона связан также магнитный момент, который векторно складывается со спиновым магнитным моментом, образуя полный магнитный момент системы. Несмотря на то, что электроны всегда входят в состав атомов и молекул магнитный момент может наблюдаться отнюдь не во всех атомах (веществах). Это обусловлено взаимодействием атомарных электронов друг с другом. Электроны, входящие в состав атомов или молекул взаимодействуют между собой так, что их индивидуальные магнитные моменты, связанные с их орбитальным движением и спином, могут как складываться, образуя увеличенный постоянный магнитный момент, так и взаимно компенсироваться. В последнем случае вещество не будет обладать парамагнетизмом, оно будет диамагнитным. Такая компенсация возникает в атомах и ионах с целиком заполненными электронными оболочками. Внешние валентные оболочки атомов обычно заполнены частично, но они неустойчивы: в результате химических реакций они либо полностью опустошаются, либо заполняются целиком, образуя устойчивые диамагнитные ионы или молекулы. Материалы, у которых не происходит компенсации магнитных моментов, называются парамагнетиками. У подавляющего большинства материалов полный магнитный момент появляется только тогда, когда там присутствуют атомы с незаполненной внутренней электронной оболочкой. Благодаря этому они могут иметь суммарный момент количества движения и магнитный момент. Такие атомы принадлежат к "переходным элементам" периодической таблицы Менделеева, например: хром, марганец, железо, никель, кобальт, палладий и платина. Кроме того все редкоземельные элементы также имеют незаполненную внутреннюю оболочку, а следовательно, являются парамагнетиками. К парамагнетикам относятся также атомы и молекулы с нечётным числом электронов (например, атомы азота, водорода, молекулы NO) и свободные радикалы химических соединений с неспаренными электронами (например, СН3); В магнитном поле магнитный момент системы может ориентироваться только определенным образом. Число его возможных ориентаций равно степени вырождения энергетического уровня (рис.1б, 1в). В поле все магнитные моменты стремятся повернуться и встать по полю. Для осуществления этого поворота каждой ориентации магнитного момента требуется совершить свою работу поворота. Это приводит к тому, что энергии уровней становятся различными, т.е. вырождение снимается. Другими словами, каждый энергетический уровень атома расщепляется в магнитном поле на магнитные подуровни - эффект Зеемана. В постоянном магнитном поле B энергетический уровень 2S+1LJ расщепляется на 2J+1 равноотстоящих подуровней, причем величина сдвига уровня зависит от квантовых чисел L, S и J данного уровня: ΔE =∙-μJB∙B (1) где μJB - проекция магнитного момента на направление поля, равная μJB = -g∙μB∙mJ (2) где μB — магнетон Бора, mJ = -J, -(J-1), …, J-1, J - магнитное квантовое число, а В простейшем случае свободного электрона L=0, J=S=1/2, mJ = ±1/2, g =2,00 и энергия E свободного электрона может принимать два значения: E1 = -g∙μB∙B/2∙ и E2 = g∙μB∙B/2 (3) Переходы между магнитными подуровнями возможны, когда квант электромагнитной энергии ћω равен разности энергий между ними: ћω = E2-E1 = gμBB (4) Переход электрона с одного подуровня на другой происходит с одновременным изменением направления спина: ΔmS = ±1. (5) Для частиц, содержащих несколько электронов, S может принимать любое кратное 1/2 значение (рис. 1б,1в), а величина g-фактора определяется суммарным значением спинового и орбитального моментов количества движения электрона и может в несколько раз отличаться от значения для свободного электрона. На практике имеют дело с макроскопическими образцами, содержащими огромное количество парамагнитных атомов или молекул. В таких системах действуют статистические законы, в соответствии с которыми большая часть парамагнитных частиц находится в состоянии с минимальной энергией. В соответствии с распределением Больцмана
населённость нижнего уровня N1 больше, чем верхнего N2. Это означает, что большинство парамагнитных атомов или молекул ориентируют свои магнитные моменты по направлению магнитного поля. Несколько меньшее число атомов располагается так, что их магнитные моменты составляют с внешним полем некоторый угол, и меньше всего атомов имеет максимальную энергию, соответствующую направлению магнитных моментов атомов против поля. Такое распределение частиц по уровням в определенном смысле обладает свойствами устойчивого равновесия, известного в обычной механике: если каким-либо способом изменить это распределение, то через некоторое время оно снова вернется в равновесное состояние. При равновесном распределении, когда большинство частиц обладает минимальной энергией, поглощение электромагнитной энергии всегда должно преобладать над ее излучением, что и наблюдается в ЭПР. Если каким-либо образом создать инверсию населённостей Взаимодействие электронов с электромагнитным внутрикристаллическим полем приводит для S≥1 к расщеплению уровней энергии с разными значениями |MS|и без магнитного поля (при B=0). В результате этого в спектре ЭПР появляется несколько линий поглощения (тонкая структура; рис. 3а). Взаимодействие электронов с магнитным моментом ядра парамагнитного атома приводит к появлению в спектре ЭПРсверхтонкой структуры. Рассмотрим атом, в котором неспаренный электрон взаимодействует с одним протоном (спин протона I=1/2). Во внешнем магнитном поле B, так же как и для электрона, будут реализовываться две ориентации магнитного момента протона: по полю MI = 1/2 и против поля MI=-1/2. Магнитный момент протона создает в месте нахождения электрона дополнительное магнитное поле ΔBI. Поэтому при напряженности внешнего магнитного поля B0 неспаренные электроны тех атомов, у которых MI = 1/2, окажутся в суммарном поле B = B0+ΔBI. В атомах, у которых MI = -1/2, величина суммарного поля равна B = B0-ΔBI. В магнитном поле энергии ядер в состояниях с MI = 1/2 и MI = -1/2 практически не различаются, поэтому число ядер в этих состояниях практически одинаково. Отсюда и число электронов, находящихся в дополнительных полях +ΔBI и -ΔBI также одинаково. Таким образом, каждый энергетический уровень неспаренного электрона расщепится на два равнозаселенных уровня (рис. 3б). Правило отбора при электронных переходах ΔMI=0. Это значит, что за время электронного перехода не происходит изменения ориентации ядерного спина. |
||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 518. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 в магнитном поле B и расщепление энергетических уровней: а – свободного электрона, б – парамагнитной частицы с несколькими электронами и со спином S=1, в – со спином S=5/2.
в магнитном поле B и расщепление энергетических уровней: а – свободного электрона, б – парамагнитной частицы с несколькими электронами и со спином S=1, в – со спином S=5/2.
 Переходы электрона из одного состояния в другое могут происходить только скачком, причем прыжок с нижнего уровня на верхний связан с поглощением, а с верхнего уровня на нижний - с выделением порции энергии (кванта), равной разности энергий E2-E1. Это и обусловливают явление ЭПР, при котором ориентированные по полю электроны, поглощая электромагнитную энергию, изменяют ориентацию магнитных моментов на обратную (рис.2).
Переходы электрона из одного состояния в другое могут происходить только скачком, причем прыжок с нижнего уровня на верхний связан с поглощением, а с верхнего уровня на нижний - с выделением порции энергии (кванта), равной разности энергий E2-E1. Это и обусловливают явление ЭПР, при котором ориентированные по полю электроны, поглощая электромагнитную энергию, изменяют ориентацию магнитных моментов на обратную (рис.2).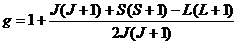 - так называемый g-фактор Ланде электрона; J, L и S - квантовые числа. Для магнитного квантового числа mJ имеется правило отбора, согласно которому возможны только переходы, при которых mJ либо остается неизменным, либо меняется на единицу ΔmJ = 0, ±1.
- так называемый g-фактор Ланде электрона; J, L и S - квантовые числа. Для магнитного квантового числа mJ имеется правило отбора, согласно которому возможны только переходы, при которых mJ либо остается неизменным, либо меняется на единицу ΔmJ = 0, ±1. , (6)
, (6) , то под действием электромагнитного поля система будет излучать энергию.
, то под действием электромагнитного поля система будет излучать энергию.