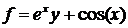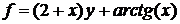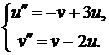Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные теоретические сведенияПод аппроксимацией обычно подразумевается описание некоторой, порой не заданной явно, зависимости или совокупности представляющих ее данных с помощью другой, обычно более простой или более единообразной зависимости. Часто данные находятся в виде отдельных узловых точек, координаты которых задаются таблицей данных. Результат аппроксимации может не проходить через узловые точки. Для обработки данных MATLAB использует различные функции интерполяции и аппроксимации данных. Одна из наиболее известных аппроксимаций — полиномиальная. В системе MATLAB определены функции аппроксимации данных полиномами по методу наименьших квадратов — полиномиальной регрессии. Это выполняет функция, приведенная ниже: – polyfit(x, y, n) – возвращает вектор коэффициентов полинома р(х) степени n, который с наименьшей среднеквадратичной погрешностью аппроксимирует функцию у(х). Под интерполяцией обычно подразумевают вычисление значений функции f(x) в промежутках между узловыми точками. Линейная, квадратичная и полиномиальная интерполяция реализуются при полиномиальной аппроксимации. В ряде случаев очень удобна сплайновая интерполяция и аппроксимация таблично заданных функций. При ней промежуточные точки ищутся по отрезкам полиномов третьей степени — это кубическая сплайновая интерполяция. При этом обычно такие полиномы вычисляются так, чтобы не только их значения совпадали с координатами узловых точек, но также, чтобы в узловых точках были непрерывны производные первого и второго порядков. Такое поведение характерно для гибкой линейки, закрепленной в узловых точках, откуда и происходит название spline (сплайн) для этого вида интерполяции (аппроксимации).  Для одномерной табличной интерполяции используется функция interpl: – yi = interp1(x, y, xi) — возвращает вектор yi, содержащий элементы, соответствующие элементам xi и полученные интерполяцией векторов х и y. Вектор х определяет точки, в которых задано значение y. – yi = interp1(x, y, xi, method) — позволяет с помощью параметра method задать метод интерполяции: – 'nearest' — ступенчатая интерполяция; – 'linear' — линейная интерполяция (принята по умолчанию); – 'spline' — кубическая сплайн-интерполяция; – 'cubic' или 'pchip' — интерполяция многочленами Эрмита. Сплайн – интерполяция используется для представления данных отрезками полиномов невысокой степени – чаще всего третьей. При этом кубическая интерполяция обеспечивает непрерывность первой и второй производных результата интерполяции в узловых точках. Реализуется сплайн-интерполяция следующей функцией: – yi = spline(x, y, xi) — использует векторы х и у, содержащие аргументы функции и ее значения, и вектор xi, задающий новые точки. Решение большинства задач интерполяции и аппроксимации функций и табличных данных обычно сопровождается их визуализацией. Она, как правило, заключается в построении узловых точек функции (или табличных данных) и в построении функции аппроксимации или интерполяции (рис.6.1). В MATLAB 6.5 совмещение функций аппроксимации с графической визуализацией доведено до логического конца — предусмотрена аппроксимация рядом методов точек функции, график которой построен. И все это выполняется прямо в окне редактора графики Property Editor. Для этого в позиции Toolsграфического окна имеются две новые команды: Basic Fitting – основные виды аппроксимации (регрессии); Data Statistics – статистические параметры данных. Команда Basic Fitting открывает окно, дающее доступ к ряду видов аппроксимации и регрессии: сплайновой, эрмитовой и полиномиальной со степенями от 1 (линейная аппроксимация) до 10. В том числе со степенью 2 (квадратичная аппроксимация) и 3 (кубическая аппроксимация) (рис.6.2).
Рисунок 6.1 – Пример визуализации процесса интерполяции
Рисунок 6.2 – Окно доступа к видам аппроксимации и регрессии
Команда Data Statistics открывает окно с результатами простейшей статистической обработки данных (рис.6.3).
Рисунок 6.3 – Окно результатов статистической обработки
Анализ поведения многих систем и устройств в динамике базируются на решении систем обыкновенных дифференциальных уравнений (ОДУ). Их, как правило, представляют в виде системы из дифференциальных уравнений первого порядка в форме Коши:
где Параметр t не обязательно означает время, хотя чаще всего решение дифференциальных уравнений ищется во временной области. Вектор b задает начальные и конечные условия. Для решения систем ОДУ в MATLAB реализованы различные методы. Их реализации названы решателями ОДУ. Решатели реализуют следующие методы решения систем дифференциальных уравнений, причем для решения жестких систем уравнений рекомендуется использовать, только специальные решатели ode45, ode23: – ode45 — одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. – ode23 — одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. В описанных далее функциях для решения систем дифференциальных уравнений приняты следующие обозначения и правила: – options — аргумент, создаваемый функцией odeset (еще одна функция позволяет вывести параметры, установленные по умолчанию); – tspan — вектор, определяющий интервал интегрирования [t0 tfinal]. Для получения решений в конкретные моменты времени t0, tl,..., tfinal (расположенные в порядке уменьшения или увеличения) нужно использовать tspan = [t0 tl ... tfinal]; – у0— вектор начальных условий; – pi, р2,.. — произвольные параметры, передаваемые в функцию F; – Т, Y — матрица решений Y, где каждая строка соответствует времени, возвращенном в векторе-столбце Т. Перейдем к описанию функций для решения систем дифференциальных уравнений: – [T, Y] = solver(@F,tspan,у0) — где вместо solver подставляем имя конкретного решателя — интегрирует систему дифференциальных уравнений вида у'=F(t,y) на интервале tspan с начальными условиями у0, @F — дескриптор ODE-функции. Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце Т; – [T, Y] = solver(@F, tspan, y0, options) — дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Технология решения дифференциальных уравнений в системе MATLAB такова: 1) Создание m–файла. Независимо от вида системы он имеет вид:
function dy = solverDE(t, y) dy = zeros(n, 1); dy(1) = f1 (t, y(1), y(2), …, y(n)); dy(2) = f2 (t, y(1), y(2), …, y(n)); …………………………… dy(n) = fn (t, y(1), y(2), …, y(n));
2) Получение решения и сопровождающий его график:
>> [T, Y] = solver(‘solverDE’, [t0 tfinal], [y10 y20 … yn0]); >> plot(T, Y)
Пусть, к примеру, требуется решить дифференциальное уравнение:
с единичными начальными условиями. Данное дифференциальное уравнение второго порядка приведем к системе дифференциальных уравнений первого порядка:
с начальными условиями у1(0)=1, у2(0)=1, у3(0)=1. Вектор
Рисунок 6.4 – Пример создания функции для решения системы ОДУ
Теперь можно вызывать функцию ode45, находящую решение нашей системы дифференциальных уравнений с начальными условиями [1,1,1] на отрезке [0,20] (рисунок 6.5)
>> y0=[1 1 1 ]; >> tspan=[0 20]; >> [T,Y]=ode45('ex21',tspan,y0); >> plot(T,Y)
Рисунок 6.5 – Результат работы программы
Для решения дифференциальных уравнений в MATLAB зарезервирована функция dsolve, которая имеет следующие форматы обращения и возвращает аналитическое решение системы дифференциальных уравнений с начальными условиями: – y=dsolve( 'Dy(x)' ), где Dу(х) – уравнение, у–возвращаемые функцией dsolve решения. – y=dsolve ('Dy(x)', 'НУ') , где Dу(х) – уравнение, НУ – начальные условия. Первая производная функции обозначается Dу, вторая производная – D2у и так далее. Функция dsolve предназначена также для решения системы дифференциальных уравнений. В этом случае она имеет следующий формат обращения: – [f,g] =dsolve('Df(x),Dg(x)', 'НУ'), где Df(x) ,Dg(x) – система уравнений, НУ – начальные условия. Решить дифференциальное уравнение (3) и использованием функции dsolve(рисунок 6.6).
Рисунок 6.6 – Пример использования команды dsolve Порядок выполнения
1. С помощью интерполяции найти значение таблично заданной функции в указанной точке таблица 6.1. 2. Выполнить аппроксимацию таблично заданной функции таблица 6.1.
Таблица 6.1– Варианты заданий
3. На отрезке [a, b] найти решение дифференциального уравнения в виде
Таблица 6.2– Варианты заданий
4. Решить систему ОДУ, представленную в таблице 6.3, при заданных начальных условиях с помощью функции dsolve.
Таблица 6.3 Варианты заданий
Содержание отчета 1. Цель занятия. 2. Листинг программы. 3. Результаты выполнения.
Контрольные вопросы
1.Для чего служит функция interp1? 2. Какой функцией реализуется сплайн-интерполяция в MATLAB? 3. Какие существуют методы решения систем дифференциальных уравнений? Практическое занятие № 7
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 205. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 (2)
(2) — начальные и конечные точки интервалов.
— начальные и конечные точки интервалов. (3)
(3) (4)
(4)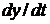 правых частей системы уравнений, вычисляем с помощью собственной функции ex21 (рисунок 6.4):
правых частей системы уравнений, вычисляем с помощью собственной функции ex21 (рисунок 6.4):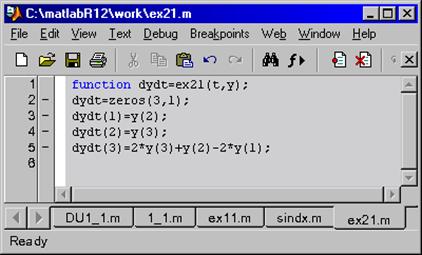


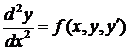 с начальными условиями
с начальными условиями  ,
,  . Варианты заданий представлены в таблице 6.2. Построить график функции.
. Варианты заданий представлены в таблице 6.2. Построить график функции.