
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА– при любых процессах в замкнутой системе ее полный момент импульса остается неизменным Б 9 Вращение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение. Связь между динамическими и кинематическими характеристиками вращения твердого тела. Вращательным наз. такой вид движения при котором каждая т. Твердого тела в процессе своего движения описывает окружность.У.с –наз.величина равная первой производной от угла поворота от времени W=dφ/dt физический смысл у.с. изменение угла поворота за единицу времени у.с. у всех т. Тела будет одинакова [1рад/с] Угловое ускорение(ε) –физическая величина числено равная изменению угловой скорости за единицу времени ε=dw/dt, W=dφ/dt ε=dw/dt=d2φ/dt связь. ε V=Wrat=dv/dt=d/dt(Wr)=r*dw/dt(ε) at=[ε*r]an=V2/r =W2*r2/ran=W2r Установим связь между угловыми характеристиками вращения всего тела и линейными характеристиками движения отдельных его точек. Для этого рассмотрим вращение диска и траекторию одной из его точек . Траекторией точки А будет окружность радиусом R . За малый интервал времени dt угловое перемещение будет равен ,а путь . Вследствие малости величин и . При вращении тела движение каждой точки характеризуется,,, кроме угловых характеристик, ещё линейными характеристиками: путь S, скорость,тангенциальноеи нормальное ускорения. Для установления связи между ними продифференцируем выражение (1) по времени т.к. и то (2) Взяв производную по времени от полученного выражения (2) получим, где, а .Тогда (3) Зная, что нормальное ускорение , после подстановки значения скорости (2) получим (3)Все величины, стоящие в формулах (1-4 )  являются векторными. При этом линейные векторные величины лежат в плоскости окружности по которой движется точка, а все угловые – вдоль оси вращения, перпендикулярной плоскости. Если положение рассматриваемой точки определить радиусом вектором, проведённым из лежащего на оси вращения начала координат О ,то вектор скорости ,а её модуль,где . Аналогично можно записать в векторной форме : Б 10 Момент инерции. Теорема Гюйгенса-Штейнера. Момент инерции и кинетическая энергия вращения твердого тела вокруг неподвижной оси. ^Момент инерции точки- величина, равная произведению массы m точки на квадрат ее кратчайшего расстояния r до оси (центра) вращения: Jz= m r2, J = m r2, кг. м2. Теорема Штейнера:Моментом инерции твердого тела относительно любой оси равен сумме момента инерции относительно оси проходящей через центр масс и произведению массы этого тела на квадрат расстояния между осями. I=I0+md2 .Величина I, равная сумме произведений элементарных масс на квадраты их расстояния от некоторой оси, наз. моментом инерции тела относительно данной оси. I=miRi2 Суммирование производиться по всем элементарным массам на которые можно разбить тело. Перейти к: навигация, поиск Кинетическая энергиявращательного движения — энергия тела, связанная с его вращением. Основные кинематические характеристики вращательного движения тела — его угловая скорость (
и кинетическая энергия
где Iz — момент инерции тела относительно оси вращения. Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерцииI1, I2 и I3. Вращательная энергия такой молекулы задана выражением
где ω1, ω2, и ω3 — главные компоненты угловой скорости. В общем случае, энергия при вращении с угловой скоростью
Б 11 Инвариантность законов динамики в ИСО. Система отсчета движется поступательно и ускоренно. Система отсчета равномерно вращается. (Материальная точка покоится в НИСО, материальная точка движется в НИСО.). Теорема Кориолиса. Си́лаКориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году и Эйлером в 1765 году. Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо. Б 12 |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 479. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
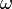 ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:


 находится по формуле:
находится по формуле: , где
, где  — тензор инерции
— тензор инерции , где
, где  — кориолисово ускорение. Соответственно, тело действует по третьемузаконуНьютона с силой противоположной направленности.
— кориолисово ускорение. Соответственно, тело действует по третьемузаконуНьютона с силой противоположной направленности.  Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.