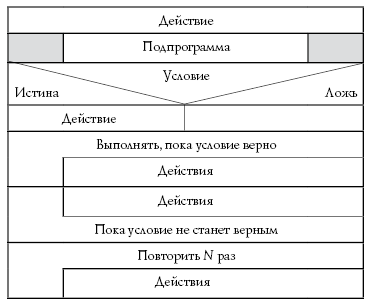
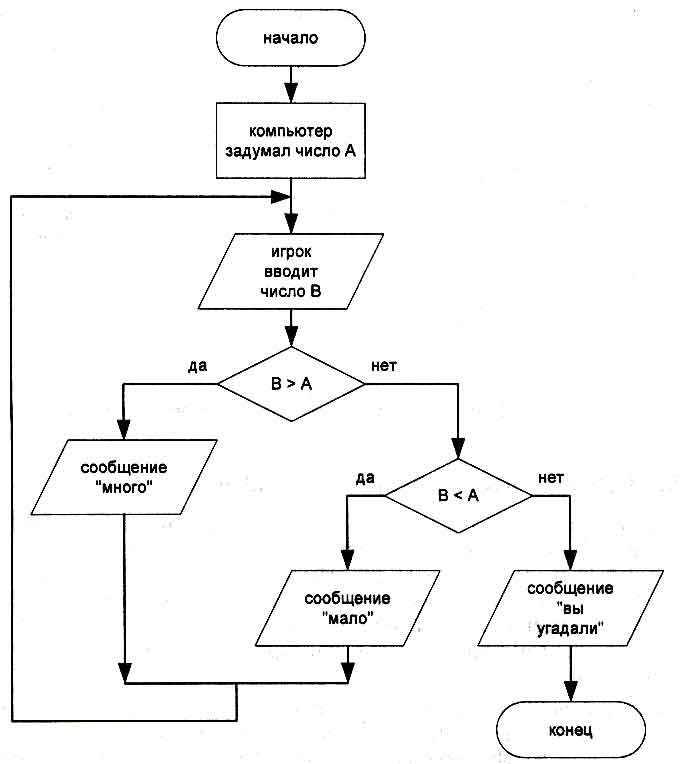
Описание алгоритма в графическом виде.

Этапы решения прикладных задач на ЭВМ: постановка задачи, построение математической модели, выбор метода решения.

Ответ:

Постановка задачи.

На данном этапе строится описательная информационная модель объекта или процесса. Поиск решения любой задачи начинается с анализа ее условий. Результатом анализа должна стать четкая постановка задачи, в которой должны быть ответы на четыре вопроса:

· Что дано?

· Что требуется?

· Какие данные допустимы?

· Какие результаты будут правильными, а какие нет?

Таким образом, четко сформулировать задачу – означает извлечь из информации об изучаемом явлении или объекте исходные данные, определить, что будет результатом. Точность и четкость постановки задачи – половина успеха ее решения. Неудачи в решении задач могут возникнуть из-за неправильно выделенных исходных или требуемых данных, когда полученные результаты не могут нас удовлетворить. Поэтому при постановке задачипрежде всего необходимо определить и перечислить все исходные и требуемые данные и затем ответить на вопрос, при каких условиях возможно получение требуемых результатов, а при каких нет. И, наконец, важно определить, какие результаты будут считаться правильными.

Разработка математической модели.

Правильность результатов решения задачи с помощью компьютера зависит, прежде всего, от правильности выбранного метода решения.Метод решения является правильным, если для любых допустимых исходных данных он приводит к получению результатов, соответствующих постановке задачи.Для решения задач с помощью компьютера соответствующим методам необходимо дать математическую интерпретацию. Как правило, строится математическая модель задачи. Создавая математическую модель, нужно записать математические соотношения (формулы, уравнения, неравенства и т.д.), связывающие результаты с исходными данными.

Выбор метода решения.

Модель решения задачи с учетом ее особенностей должна быть доведена до решения при помощи конкретных методов решения. Само по себе математическое описание задачи в большинстве случаев трудно перевести на язык машины. Выбор и использование метода решения задачи позволяет привести решение задачи к конкретным машинным операциям. При обосновании выбора метода необходимо учитывать различные факторы и условия, в том числе точность вычислений, время решения задачи на ЭВМ, требуемый объем памяти и другие.Одну и ту же задачу можно решить различными методами, при этом в рамках каждого метода можно составить различные алгоритмы.

2.Понятие и суть алгоритма. Формы представления (способы описания) алгоритмов.Примеры.

Ответ:

Алгоритм – последовательность действия для достижения поставленной цели.

Формы представления:

· Словесная (формульно-словесная)

· Псевдокод (формальный алгоритмический язык)

· Схематическая

o Графические блок-схемы

o Структурограммы (диаграммы Насси-Шнейдермана)

· Язык программирования

Словесно-формульное представление алгоритма

Особенности:

1. Используется естественный язык, математические и иные обозначения.

2. Ориентировано исключительно на человека.

3. Описание алгоритма не формализуемо (алгоритм не может быть преобразован в программу).

4. Многословность.

5. Допускает неоднозначность толкования.

6. Отсутствие наглядности.

Пример:

1. Открыть файл

2. Считать строку

3. Записать в другой файл

4. Закрыть файл

Описание алгоритма в виде псевдокода.

Особенности:

1. Компактный (зачастую неформальный) язык описания алгоритмов, использующий ключевые слова языков программирования;

2. Опускает специфический синтаксис и несущественные (для понимания человека) подробности ;

3. Псевдокод обычно опускает детали, несущественные для понимания алгоритма человеком;

4. Главная цель использования – обеспечить понимание алгоритма человеком;

5. Слабо формализуем, сложен для прямого преобразования в программу

Пример:

1. Начало

2. Ввести данные

3. Пока переменная меньше 10

4. Прибавить 1

5. Иначе вывести «Ошибка»

6. Конец

Описание алгоритма в графическом виде.

Структурограмма (диаграмма Насси-Шнейдермана).

Особенности:

1. Отсутствие дополнительных соединительных линий.

2. Удобно использовать при последовательной детализации алгоритма (от "крупного" к "мелкому").

3. Наглядность.

4. Компактность (по сравнению с блок-схемами).

5. Простота использования.

6. Гарантированно получаем алгоритм, отвечающий принципам структурного программирования.

Пример:

Блок-схема

Особенности:

1. Вершины трех типов: функциональная (1 вход, 1 выход); предикатная (1 вход, 2 выхода); объединяющая (2 входа, 1 выход).

2. Нельзя использовать элементы языка программирования, все выражения записываются по математическим правилам, кроме присваивания (:=) и логического сравнения на равенство (=).

Пример:

3.Основные свойства алгоритма. Примеры.

Ответ:

Дискретность.

· Решение задачи – как последовательность действий (шагов, этапов).

Пример: