
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непосредственный подсчет вероятностейСтр 1 из 2Следующая ⇒ Предисловие
Цель предлагаемой работы — помочь, изучающим теорию вероятностей, приобрести навыки решения стандартных задач. Первая часть методических указаний содержит краткое изложение основных понятий и формул по начальному разделу теории вероятностей «Случайные события», изложение теории сопровождается решением типовых задач. Во второй части даны варианты индивидуальных заданий, которые, в основном, повторяют задания из предыдущих изданий методических указаний, составленных М.Е. Хацкевич, Г.П. Бизяевой, О.Л. Сидоровой.
Вопросы для повторения 1. Какие соединения называются размещениями, перестановками, сочетаниями? По каким формулам они вычисляются? 2. Как определяются понятия опыт, события? Какие события называются достоверными, невозможными? Как определяются действия с событиями А + В; А · В; Ā ? 3. Чему равны события А + Ā; А · Ā; A + D; A · D; A + H; A · H? 4. Какие события называются несовместными, полной группой событий? 5. Какие определения вероятности события Вы знаете? Сформулируйте классическое, статистическое, геометрическое определения вероятности. Когда они применяются? 6. Условная вероятность. Вероятность произведения событий. Зависимые и независимые события. 7. Вероятность суммы для несовместных и совместных событий. 8. Вероятность противоположного события. 9. Формула полной вероятности. 10. Формула гипотез (Бейеса).
Основные понятия
Под опытом (испытанием) понимается осуществление определенных условий, которые могут быть повторены сколь угодно раз. Возможные результаты опыта называются событиями, обозначаются латинскими буквами А, В, С, …  Событие, которое в данном опыте обязательно произойдет — достоверное событие (D); событие, которое в данном опыте произойти не может — невозможное (H). Произведение событий А · В = С есть событие, состоящее в наступлении обоих событий А и В. Сумма событий А + В = С есть событие, состоящее в наступлении хотя бы одного из событий А или В. Событие, противоположное А, обозначается Ā (не А). События А и В несовместны, если А · В = Н. События А (k=1,2, …,n) образуют полную группу событий, если Пример 1.1. При каких событиях А и В возможно равенство А + В = А? Решение. А + В событие, состоящее в наступлении хотя бы одного из событий А или В. Если А + В = А, то событие В не изменяет события А, а потому В является частью события А. Например, из таблицы случайных чисел выбирают число. А — событие, состоящее в том, что число делится на 2; В — число делится на 4. А + В=А, так как если число делится на 4, то оно делится на 2. Пример 1.2. Событие А — хотя бы одно из четырех изделий бракованное, событие В — бракованных изделий среди них не менее двух. Что означают события Решение. Этим понятиям посвящены задачи № 1 в индивидуальных заданиях.
Непосредственный подсчет вероятностей Непосредственный подсчет вероятностей может быть произведен в том случае, когда результат опыта можно представить в виде полной группы событий, которые попарно несовместные и равновозможные
n — число всех возможных исходов опыта; m — число исходов благоприятствующих событию А.
Пример 2.1. Брошены две игральные кости. Какова вероятность, что сумма очков, выпавших на верхних гранях, равна 5? Решение. Событие А — сумма выпавших очков на двух костях равна 5. Число всех возможных исходов n = 36, так как 6 исходов на первой кости могут сочетаться с каждым из 6 исходов на второй кости. Число благоприятных исходов m = 4: (1; 4), (2; 3), (3; 2), (4; 1), поэтому
Пример 2.2. В партии из l изделий бракованных k штук. Определить вероятность того, что среди выбранных наудачу для проверки s изделий ровно r окажутся бракованными. Решение. Событие А — из выбранных s изделий ровно k бракованных. Число возможных способов взять s изделий из l равно n =
Напомним, что l! =
Геометрические вероятности Геометрическое определение вероятности используется в том случае, когда результат испытания определяется случайным положением точек в некоторой области, причем любые положения точек в этой области равновозможные. Если размер всей области S, а размер части этой области, попадание в которую благоприятствует данному событию, есть Область может иметь любое число измерений, поэтому Пример 3.1. В течение промежутка времени от 11 ч до 11ч 30 мин должен последовать телефонный звонок. Какова вероятность, что звонок последует в последние 10 минут указанного промежутка. Решение. Будем рассматривать промежуток времени от 11ч до 11ч 30мин, как отрезок АВ длиной 30 единиц, промежуток от 11ч 20мин до 11ч 30мин (последние 10мин) как отрезок СВ длиной 10 единиц.
А С В Рис. 1.
Вероятность того, что звонок произойдет в последние 10мин, в геометрической схеме означает вероятность того, что случайно брошенная точка в отрезок АВ попадет на отрезок СВ. Эта вероятность, очевидно, равна
Пример 3.2. Два парохода должны подойти к одному и тому же причалу. Время прихода каждого парохода независимо от другого и равновозможно в течение данных суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода — один час, а второго — два часа. Решение. Воспользуемся геометрической схемой. Пусть х — время прихода первого парохода, у — второго. Все возможные комбинации прихода пароходов к причалу изобразятся точками квадрата
24
Строим область, благоприятствующую событию А, это множество решений системы неравенств На рис. 2 она заштрихована. Площадь квадрата S = 24² = 576; площадь заштрихованной части
С понятием геометрической вероятности связаны задачи № 3 в индивидуальных заданиях.
Основные теоремы 1. Р(А + В) = Р(А) + Р(В), если А · В = Н, то есть А и В — несовместны. 2. Р(А · В) = Р(А) Р(В/A) = P(B) P(A/B). Условной вероятностью Р(А/В) события А называется вероятность появления этого события, вычисленная при условии, что имело место событие В. Р(А · В · С) = Р(А) Р(В/A) P(C/A·B) 3. Если события независимые, то Р(А · В) = Р(А)Р(В). 4. Р(Ā) = 1 ‑ Р(А). Пример 4.1. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятности следующих событий: в мишени две пробоины; в мишени одна пробоина; в мишени хотя бы одна пробоина. Решение. Пусть А1 — событие, состоящее в том, что первый стрелок попал в цель, А2 — второй стрелок попал в цель. По условию Р(А1) = 0,7; Р(А2) = 0,8; А1 и А2 — независимы. 1. Событие А — в мишени две пробоины: А = А1·А2, поэтому Р(А) = Р(А1·А2) = Р(А1)·Р(А2) = 0,7·0,8 = 0,56. 2. Событие В — в мишени одна пробоина: В = А1Ā 2+ Ā1А2. Тогда Р(В) = Р(А1)Р(Ā2) + Р(Ā1)Р(А2); P(Ā1) = 1 ‑ P(А1) = 0,3; P(Ā2) = 0,2; P(B) = 0,7 · 0,2 + 0,8 · 0,3 = 0,38. 3. Событие С — в мишени хотя бы одна пробоина (или одна или две).Очевидно, С = А + В, А и В несовместны. Р(С) = Р(А) + Р(В) = 0,56 + 0,38 = 0,94.
Если Р(А) и Р(В) предварительно не были найдены, проще найти вероятность противоположного события —
Пример 4.2. Слово РЕКЛАМА разрезано на отдельные буквы, они перемешаны. Выбираются одна за другой три буквы. Какова вероятность, что получится слово МАК? Решение. Чтобы получилось заданное слово (событие А) надо первой вынуть букву М (событие А1), второй — букву А (событие А2), третьей — букву К (событие А3) А = А1 · А2 · А3; Р(А) = Р(А1) ·Р(A2/А1) ·Р(А3/А1А2), Р(А1) =
Р(А3/А1А2) = Р(А) = Формула полной вероятности Если исходы опыта (гипотезы): Г1, Г2,… , Гn образуют полную группу попарно независимых событий, то вероятность появления события А находится по формуле полной вероятности
Пример 5.1. В тире имеется пять ружей, вероятности попадания из которых равны соответственно 0,5; 0,6; 0,7; 0,8; и 0,9. Определить вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу. Решение. Событие А — попадание при одном выстреле. Гипотезы — стреляющий выбрал первое ружье(Г1), второе — (Г2) и т.д. Так как ружье выбирается на удачу, их пять штук, Р(Гi) = Р(А) =
Пример 5.2. На сборку поступают детали с трех автоматов. Первый дает 25%, второй — 30% и третий — 45% деталей, поступающих на сборку. Первый автомат допускает 1% нестандартных деталей, второй — 2%; третий — 3%. Найти вероятность поступления на сборку нестандартной детали. Решение. Событие А — деталь, поступившая на сборку, нестандартная. Пусть Г1 – деталь с первого автомата, Р(Г1) = 0,25 (т.к. их 25%), аналогично, Р(Г2) = 0,30; Р(Г3) = 0,45. Р(A/Г1) = 0,01 (вероятность быть детали нестандартной, если она изготовлена на первом автомате). Р(A/Г2) = 0,02; Р(A/Г3) = 0,03; Р(А) =
Задачи №8 в индивидуальных заданиях могут быть решены по формуле полной вероятности.
|
||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 512. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
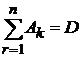 . Отметим, что А · Ā = H, А + Ā = D.
. Отметим, что А · Ā = H, А + Ā = D.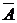 и
и  ?
? ,
,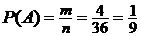 .
.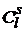 . Благоприятствующими событию А являются случаи, когда из общего числа k бракованных изделий взято r штук (это можно сделать
. Благоприятствующими событию А являются случаи, когда из общего числа k бракованных изделий взято r штук (это можно сделать 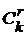 способами), а остальные
способами), а остальные 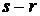 изделий не бракованные, т.е. они взяты из общего числа
изделий не бракованные, т.е. они взяты из общего числа 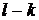 (таких способов
(таких способов 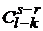 ). Поэтому m =
). Поэтому m = 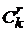 ·
· 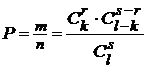 .
.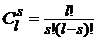 — число сочетаний из l элементов по s.
— число сочетаний из l элементов по s.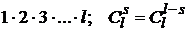 .
.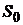 , то вероятность равна
, то вероятность равна 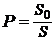 .
.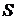 и
и 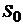 могут представлять собой длины отрезков, площади, объемы.
могут представлять собой длины отрезков, площади, объемы.
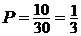 .
.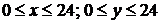 (рис. 2). Событие А — один из пароходов ожидает освобождение причала. Оно может состояться лишь в том случае, если момент у прихода второго парохода не более часа отличается от момента прихода первого (
(рис. 2). Событие А — один из пароходов ожидает освобождение причала. Оно может состояться лишь в том случае, если момент у прихода второго парохода не более часа отличается от момента прихода первого ( 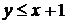 ), и момент прихода первого не более двух часов отличается от момента прихода второго (
), и момент прихода первого не более двух часов отличается от момента прихода второго ( 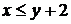 ).
). y
y


 0 (2;0) 24 x
0 (2;0) 24 x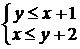
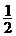 (23)2 ‑ (22)2 = 69,5.
(23)2 ‑ (22)2 = 69,5.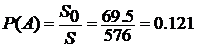 .
.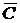 (в мишени нет пробоин):
(в мишени нет пробоин):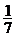 , ( n = 7 – всего букв; М встречается 1 раз m = 1),
, ( n = 7 – всего букв; М встречается 1 раз m = 1),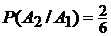 – вероятность вынуть букву А, если буква М вынута. n = 6; m = 2 (осталось шесть букв, из них две буква А),
– вероятность вынуть букву А, если буква М вынута. n = 6; m = 2 (осталось шесть букв, из них две буква А),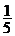 – вероятность вынуть букву К, если А и М вынуты.
– вероятность вынуть букву К, если А и М вынуты.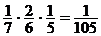 .
. .
.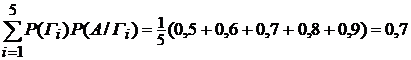 .
.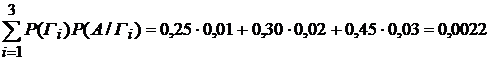 .
.