
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Приближенные методы решения уравнений.Стр 1 из 2Следующая ⇒ Министерство образования и науки РФ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ (МИИГАиК)
Факультет дистанционных форм обучения Заочное отделение Г.П.Емгушева, М.Д.Улымжиев
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ по курсу: «Высшая математика» Для студентов 3 курса всех специальностей
Москва 2016 Составители: Емгушева Г.П. – кандидат физико-математических наук, доцент кафедры «Высшая математика» МГУГиК. Улымжиев М.Д. – кандидат физико-математических наук, доцент кафедры «Высшая математика» МГУГиК.
«Вычислительная математика»: учебно-методическое пособие по курсу «Высшая математика» для студентов 3 курса всех специальностей факультета дистанционных форм обучения. – М.: МГУГиК, 2016, 37с.
Учебно-методическое пособие разработано в соответствии с утвержденной программой курса «Высшая математика», рекомендованы кафедрой высшей математики и утверждены к изданию Методической комиссией факультета дистанционных форм обучения МГУГиК.
Учебно-методическое пособие представляет собой руководство к выполнению лабораторно-практических работ по курсу «Вычислительная математика». Материал разбит на шесть параграфов, в которых содержатся необходимые теоретические сведения по темам: приближенные методы решения уравнений, численные методы решения уравнений,интерполирование, аппроксимация функций по методу наименьших квадратов, численное интегрирование с использованием формул прямоугольников, трапеций и Симпсона, квадратурная формула Гаусса, сопровождающиеся чертежами. Приводятся решения типичных примеров. В конце каждого параграфа даны вопросы для самопроверки. 
Рецензенты: профессор кафедры «Высшая математика» МГУГиК Е.Г. Маркарян, доцент кафедры «Теория вероятностей и математическая статистика» Финансового Университета при правительстве РФ О.А. Баюк. Приближенные методы решения уравнений.
При постановке математической задачи возникает вопрос о методе ее решения. Точный метод решения иногда или не нужен, или им не всегда удается воспользоваться, достаточно найти приближенное решение с определенной степенью точности. В этом случае применяют численные методы решений, это относится к решению некоторых трансцендентных уравнений, то есть уравнений, в которых неизвестная Пусть задано уравнение где функция Приближенное нахождение изолированных корней уравнения (1.1) складывается из двух этапов: 1. Отделение корней, то есть установление интервалов изоляции корней, внутри каждого из которых содержится только один корень уравнения. 2. Уточнение корней, то есть доведение их до заданной степени точности. Первый этап осуществляется графически или аналитически, где используется известная из курса математического анализа теорема Больцано- Коши: Теорема. Если непрерывная функция Заметим, что этот корень будет единственным, если функция На втором этапе уточнение корней нелинейных уравнений можно проводить, используя различные итерационные методы. Рассмотрим примеры. Пример 1.1. Решить графически уравнение Решение. Запишем уравнение в виде
1
Абсцисса точки пересечения графиков этих функций Пример 1.2. Отделить аналитически корни уравнения Решение. Обозначим
Следовательно, уравнение имеет один действительный корень, лежащий в промежутке
Замечание. При решении примера 1.2 применили итерационный метод, суть которого заключается в следующем. На каждом из интервалов изоляции корня |
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 380. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 находится под знаком трансцендентных функций, алгебраических уравнений степени выше третьей, приближенному вычислению интегралов, рядов и т.д.
находится под знаком трансцендентных функций, алгебраических уравнений степени выше третьей, приближенному вычислению интегралов, рядов и т.д. , (1.1)
, (1.1)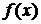 определена и непрерывна на интервале
определена и непрерывна на интервале  (конечном или бесконечном). Допустим, что уравнение (1.1) имеет лишь изолированные корни, то есть для любого корня найдется окрестность, не содержащая других корней уравнения.
(конечном или бесконечном). Допустим, что уравнение (1.1) имеет лишь изолированные корни, то есть для любого корня найдется окрестность, не содержащая других корней уравнения.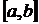 , то есть
, то есть  , то внутри отрезка
, то внутри отрезка  одного знака внутри отрезка
одного знака внутри отрезка  .
. . Построим графики функций
. Построим графики функций  .
.

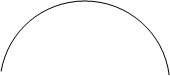
 Y
Y 


 0
0 
 X
X , что является приближенным значением корня заданного уравнения.
, что является приближенным значением корня заданного уравнения. .
.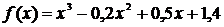 . Составим таблицу знаков функции
. Составим таблицу знаков функции 



 . Для уточнения корня, найдем первую и вторую производную.
. Для уточнения корня, найдем первую и вторую производную. 
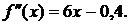 В промежутке
В промежутке 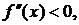 значит,
значит,  сохраняют знаки, то есть промежуток
сохраняют знаки, то есть промежуток  функция
функция  2)
2)  3)
3)  .
.