
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯСтр 1 из 3Следующая ⇒ Курсовая работа По дисциплине «Моделирование экономических процессов» Вариант 15
Калининград 2017 г. АННОТАЦИЯ В данной курсовой работе мы рассматриваем пример решения задачи линейного программирования “Оптимальная организация работы предприятия, выпускающего два вида продукта” с использованием базовой технологии и встроенных функций EXCEL 2010. Группа разработчиков выбрала эту систему по той причине, что на большинстве ПК EXCEL входит в базовую комплектацию Microsoft Office, а следовательно для расчетов не потребуется покупать новый софт и тратить на это денежные средства. В курсовой работе подробно рассмотрены этапы построения модели с использованием табличного процессора EXCEL. БЛАНК ЗАДАНИЯ Вариант № 15 Разработать математическую модель предприятия, выпускающего два вида продукции из двух видов сырья с целью решения задачи увеличения выпуска продукции как за счет приобретения нового оборудования и сверхурочных часов работы
На предприятии производятся два вида продукции из двух видов сырья. Производство единицы продукта 1 (первого вида) приносит предприятию доход, равный 10 единицам, а производство единицы продукта 2 (второго вида) - доход в 8 единиц. Переработка сырья производится аппаратами двух типов, которые условно называются в дальнейшем машинами и агрегатами. На переработке сырья первого вида занято пять машин, причем производственные условия не допускают, чтобы суммарное время использования машин на этой работе превышало 40 ч (за некоторый период). На переработке сырья второго вида занято 25 агрегатов; суммарное время их использования в течение того же периода не должно превышать 200 ч. При производстве единицы продукта 1 на переработку сырья первого вида затрачивается 4 ч и на переработку сырья второго вида - 9 ч, в то время как производство единицы продукта 2 требует затраты 3 ч на переработку каждого из видов сырья.  На предприятии принимается решение увеличить выпуск продукции как за счет приобретения нового оборудования тех типов, что и имеющиеся, так и за счет сверхурочных часов работы. Максимальное число сверхурочных часов, приходящихся на период, равно восьми, причем эти часы должны распределяться на переработку первого и второго видов сырья равномерно. Доплата за час сверхурочной работы на переработке любого из видов сырья одинакова; полная оплата за час сверхурочной работы равна 2 единицам. Повышение затрат за период, связанный с приобретением одной машины, перерабатывающей сырье первого вида, составляет 10 единиц. Агрегаты, перерабатывающие сырье второго вида, дополнительно не приобретаются.
Необходимо максимизировать доход от выпуска продукции.
Задачу максимизации дохода от выпуска продукции можно записать как задачу математического программирования:
Здесь через
4.1. Сформировать блок-схему алгоритма решения поставленной задачи. 4.2. Разработать программу решения поставленной задачи в средеVisual Basic 6.0 или в любой другой среде (по выбору студента). 4.3. С использованием базовой технологии Excel 2000 сформировать таблицу исходных данных (взамен выполнения п. 4.2) 4.4. С использованием встроенных функций Excel 2000 произвести расчет и решение поставленной задачи оптимизации для пяти различных вариантов набора исходных данных с учетом поставленных ограничений 4.5. Представить полученные результаты в виде графиков и диаграмм. СОДЕРЖАНИЕ
ЦЕЛИ ВЫПОЛНЕНИЯ РАБОТЫ. 6 МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. 6 ОПИСАНИЕ И ПОСТРОЕНИЕ МОДЕЛИ. 7 Целочисленное линейное программирование. 7 Обоснование выбранного подхода к моделированию.. 7 Описание концептуальной модели. 8 Описание элементов и ограничений решаемой задачи. 9 РЕШЕНИЕ ЗАДАЧИ. 10 Блок-схема алгоритма решения задачи. 10 Ввод данных. 11 Установка ограничений. 11 Ввод целевой функции. 12 Поиск решения. 12 Построение графиков. 15 Анализ полученных данных. 17 ЗАКЛЮЧЕНИЕ. 17 СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ. 18
1. Получить практические знания, при применении методов решения задач линейного программирования. 2. Построение модели. 3. Решение задачи методом линейного программирования. 4. Анализ модели. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ 1. Графический метод решения задачи линейного программирования. Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного простран6тва, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трех изобразить графически вообще невозможно. 2. Симплекс-метод решения задач линейного программирования. Отыскание оптимального решения с использованием симплекс – метода сводится к последовательному направленному перебору вершин многогранника, образованного ограничениями при котором монотонно увеличивается (уменьшается) значение целевой функции. 2.1. Отыскание базисного решения – некой точки А(рис.2) лежащей на функции; 2.2. Отыскание опорного решения – некой точки B (рис. 2) принадлежащей области, образованной ограничениями; 2.3. Отыскание оптимального решения – некой точки С (рис. 2) принадлежащей той – же области, и в которой целевая функция достигает своего экстремума. 3. Метод полного перебора базисных решений задачи линейного программирования. 4. Нецелочисленное линейное программирование. 5. Целочисленное линейное программирование. При решении некоторых задач линейного программирования бывает необходимо получить целочисленное решение, которое находится методами целочисленного линейного программирования. Задача целочисленного линейного программирования это задача, где некоторые или все переменные должны принимать строго целочисленные значения, а целевая функция и ограничения – линейные. Задачу целочисленного линейного программирования можно решить как задачу линейного программирования, а затем округлить полученное решение. Однако такой способ допустим только при условии, что значения переменных настолько большие, что погрешностью, вызываемой округлением можно пренебречь. Если же в результате решения переменная принимает малое значение, то ее округление может привести к очень далекому от оптимального решения. Применяются два способа решения задач ЦЛП – метод отсечений и метод ветвей и границ.
Для решения данной задачи необходимо применить ЦЛП-метод, т.к. при расчётах используются только целочисленные переменные. |
||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 302. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
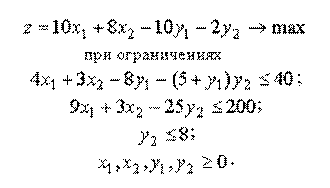
 и
и  обозначены соответственно искомые количества производимых продуктов первого и второго видов, через
обозначены соответственно искомые количества производимых продуктов первого и второго видов, через 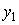 - количество приобретаемых дополнительных машин для переработки сырья первого вида и через
- количество приобретаемых дополнительных машин для переработки сырья первого вида и через 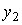 - число часов сверхурочной работы. Целевая функция представляет собой величину суммарного дохода. Первое ограничение связано с невозможностью превысить лимит времени на переработку сырья первого вида, второе - с невозможностью превысить лимит времени на переработку сырья второго вида, третье ограничение и условие неотрицательности переменных самоочевидны.
- число часов сверхурочной работы. Целевая функция представляет собой величину суммарного дохода. Первое ограничение связано с невозможностью превысить лимит времени на переработку сырья первого вида, второе - с невозможностью превысить лимит времени на переработку сырья второго вида, третье ограничение и условие неотрицательности переменных самоочевидны.