
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследовать средствами дифференциального исчисления функцию. Построить график. ⇐ ПредыдущаяСтр 2 из 2
1. 2.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ РЕШЕНИЕ ЗАДАЧИ ТИПА 1 Задача. Найти указанные пределы. 1) Решение. Здесь сталкиваемся с неопределенностью Объяснение. Вторые и третьи слагаемые скобок числителя и знаменателя при
2) Решение. В данном случае для освобождения от неопределенности
Решение примера будет выглядеть следующим образом:
УКАЗАНИЕ.При решении примеров, содержащих обратные тригонометрические функции, пользуются заменой, позволяющей перейти к пределу с тригонометрическими функциями: arcsin x=t, тогда x=sint
ПРОИЗВОДНАЯ
РЕШЕНИЕ ЗАДАЧИ ТИПА 2
УКАЗАНИЕ.При решении последующих примеров, кроме таблицы производных основных элементарных функций, будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции. Задача. Вычислить производные заданных функций. 1. Решение.y’=
2. Решение. y’
3. Решение.y’=
4. Решение.Функция задана неявно. Продифференцируем обе части равенства как функцию от х, затем выразим
 ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ РЕШЕНИЕ ЗАДАЧИ ТИПА 3 Задача. Провести полное исследование заданных функций и построить их графики: 1) Решение. 1. Областью определения данной функции являются все действительные значения аргумента D(y): R, E(y)=R а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
2. Исследуем функцию на экстремумы и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки первого рода Разбиваем область определения этими точками на части и по изменению в них знака производной функции выявляем промежутки ее монотонности и наличие экстремумов:
3. Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку второго рода
Значение
4. Выясним наличие у графика заданной функции асимптот. Для определения параметров уравнения асимптоты
Имеем
Таким образом, у графика заданной функции наклонных асимптот нет. 5. Для построения графика в выбранной системе координат изобразим точки максимума
2) Решение. 1. Область определения.
2. Исследование функции на непрерывность и классификация точек разрыва. Заданная функция непрерывна всюду, кроме точки
Итак, точка 3. Исследование функции на экстремум и промежутки монотонности.
4. Исследование графика функции на выпуклость, вогнутость, точки перегиба.
Поскольку
Очевидно, что при 5. Исследование графика на наличие наклонных асимптот.
Таким образом, прямая 6. Построение графика. Очевидно, график пересекает оси координат в точках
Вопросы к зачету Примерные вопросы для подготовки к зачету 1. Функции, способы их задания, классификация. 2. Окрестность точки. Предел последовательности. 3. Односторонние пределы. Необходимые и достаточные условия существования предела. Геометрический смысл предела. 4. Определение предела функции. 5. Теоремы о пределах (свойства пределов). 6. Первый замечательный предел. 7. Второй замечательный предел, его обоснование, применение в финансовых вычислениях. 8. Непрерывность функции в точке и на отрезке. 9. Непрерывность основных элементарных функций. 10.Точки разрыва функций. 11.Производная функции, ее геометрический и механический смысл. 12.Основные формулы дифференцирования. 13.Дифференциал функции одной переменной. Определение, условия существования, геометрический смысл, свойства. 14.Правило Лопиталя, его использование для раскрытия неопределенностей при нахождении пределов. 15.Монотонные функции. Необходимый и достаточный признаки монотонности функции. 16.Локальный экстремум функции. Необходимый признак экстремума функции. 17.Необходимый и достаточный признаки существования точки перегиба. 18.Асимптоты графика функции. Общая схема исследования функции и построения графика. 19.Производные неявных функций и производные высших порядков. 20.Производные сложной функции нескольких переменных. Приложение 1
Таблица производных основных элементарных функций
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 329. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби переменной
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби переменной  в старшей степени:
в старшей степени:
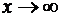 являются бесконечно малыми величинами, поэтому их пределы равны 0.
являются бесконечно малыми величинами, поэтому их пределы равны 0.
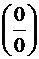 будем использовать первый замечательный предел и его очевидные следствия:
будем использовать первый замечательный предел и его очевидные следствия:




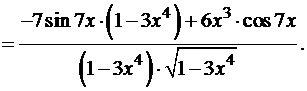

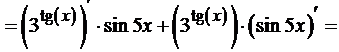
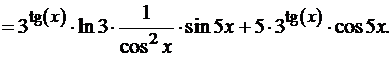




 .
.

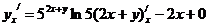
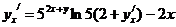






 .
.


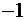







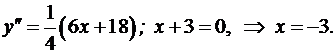
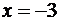 . Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:
. Разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

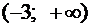



 воспользуемся формулами
воспользуемся формулами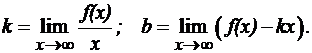

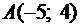 , минимума
, минимума  , перегиба
, перегиба  , и точку
, и точку 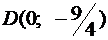 пересечения графика с осью
пересечения графика с осью  . С учетом результатов предыдущих исследований строим кривую:
. С учетом результатов предыдущих исследований строим кривую:


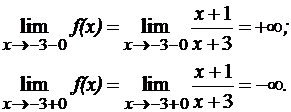

 следовательно функция не имеет точек экстремума. Так как
следовательно функция не имеет точек экстремума. Так как  для всех точек из
для всех точек из  , то функция возрастает во всей области определения.
, то функция возрастает во всей области определения.
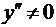 , график не имеет точек перегиба.
, график не имеет точек перегиба. , а при
, а при 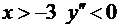 . Следовательно, график функции вогнутый при
. Следовательно, график функции вогнутый при  и выпуклый при
и выпуклый при  .
.
 является горизонтальной асимптотой графика.
является горизонтальной асимптотой графика. и имеет вид:
и имеет вид: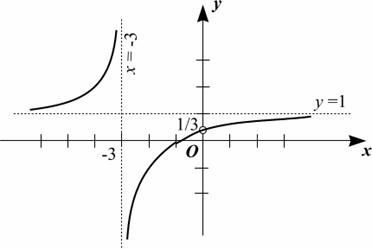



 .
.
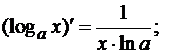
 .
.
 ;
;
 ;
;
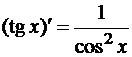 ;
;

 ;
;
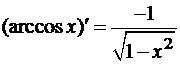 ;
;
 ;
;

 ;
;

 ;
; ;
; ;
; , где
, где  , т.е.
, т.е.  , и каждая из функций
, и каждая из функций  ,
, 
 .
.