
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Потенциальная энергия при гравитационном взаимодействии ⇐ ПредыдущаяСтр 2 из 2 Работа тела при падении A = mgh, или A = U – U0. Для случая гравитационного взаимодействия между массами M и m, находящимися на расстоянии r друг от друга, потенциальную энергию можно найти по формуле На рис. 5.4 изображена диаграмма потенциальной энергии гравитационного притяжения масс M и m.
Рис. 5.4
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и (рис. 3.1):
где β– коэффициент затухания.
Рис. 3.1 Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
Выясним физический смысл χиβ. Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Билет 21 1) Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести.
Квазиупругая сила-сила F, направленная к центру О , величина которой пропорциональна расстоянию r от центра О до точки приложения силы. численно F= cr, где с — постоянный коэффициент. силы, возникающие при малых деформациях упругих тел 2) Мощность, физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.  [N]=Вт Билет 22 1) Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
2) Сила сопротивления-сила, препятствующая движению тела или материальной точки в среде
K -коэффициент сопротивления, зависящий от формы, размеров, поверхности тела и свойств среды. В СИ он выражается в Н.с/м и определяется опытным путем
Билет N23. 1. Сложение взаимно-перпендикулярных гармонических колебаний. Рассмотрим результат сложения колебаний одинаковой частоты ,происходящих во взаимно перпендикулярных направлениях. Начальную фазу первого колебания примем = 0.
2.Момент импульса твердого тела относительно оси: В тех случаях, когда твердое тело вращается вокруг неподвижной оси, обычно оперируют с понятием момента импульса относительно оси. Момент импульса
Билет N24. 1. Гармонические колебания - колебания, происходящие по закону синуса или косинуса.
Сложение гармонических колебаний одного направления равных частот: Сложим гармонич. колебания одного направления и одинаковой частоты и построим векторные диаграммы этих колебаний Т.к. векторы А1 , А2 -вращаются с одинаковой угловой скоростью, то разность фаз будет постоянной. Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой что и складываемые колебания. Амплитуда зависит от разности фаз. В результате сложения колебаний мало отличающихся по частоте получаются колебания с периодически меняющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонич. колебаний с близкими частотами, наз. биениями. Период биений Амплитуда биений Частота биений 2. Квазиупругая сила: Выражение для консервативной силы вблизи положения равновесия
В СИ измеряется в Ньютонах,[ Н ].
Билет 25 1.Совокупность тел, выделенная для рассмотрения, называется механической системой. Система тел, взаимодействующих только между собой, называется замкнутой. Импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени (n-число материальных точек (тел), входящих в систему)
2. Фазовая кривая – графическое представление динамической системы Для вращательного движения:
W=W0+βt => t= =>
W-угловая скорость [рад/сек]
Билет 26 1.Свободные затухающие колебания. Затухающие колебания описываются уравнением: x’’+2bx’+w02x=0. 2b=r/m, w02=k/m, где r - коэффициент сопротивления, k - коэффициент квазиупругой силы. w02 - собственная частота системы. w=Öw02-b2|, x=a0e-btcos(wt+a),период затухающих колебаний: T=2p/(Öw02-b2|). Скорость затухания колебаний определяется величиной b, которую называют коэффициентом затухания.
2. Величина, равная dA=Fds, называется работой, совершаемой силой F на пути ds. Работа - физическая величина (мера), характеризующая изменение энергии в механике. Работа измеряется в Джоулях. (Дж) 1 Дж=1
Билет 27
1. Декремент и логарифмический декремент затухания. Декрементом затухания называется отношение значений амплитуд, соответствующим моментам времени, отличающимся на период: a(t)/(a(t+T))=ebT. Логарифмический декремент затухания: l=bT. Добротность колебательной системы. Для характеристики колебательной системы употребляется величина Q=p/l называемая добротностью системы. С ростом коэффициента затухания период увеличивается.
2. Коэффициент упругости (иногда называют коэффициентом Гука, коэффициентом жёсткости или жёсткостью пружины) — коэффициент, связывающий в законе Гука удлинение упругого тела и возникающую вследствие этого удлинения силу упругости. Применяется в механике твердого тела в разделе упругости. Обозначается буквой khttp://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8 - cite_note-1. Имеет размерность Н/м или кг/с2 (в СИ). Коэффициент упругости численно равен силе, которую надо приложить к пружине, чтобы её длина изменилась на единицу расстояния.
Билет 28
физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшится в е раз или безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных амплитуд колеблющейся величины в одну и ту же сторону
Билет 29 1. W= Β= S=R *
2. Фазовая кривая – графическое представление динамической системы Для вращательного движения:
W=W0+βt => t= =>
W-угловая скорость [рад/сек]
Билет 30 1.Свободные незатухающие колебания – это гармонические колебания, происходящие под действием только возвращающей силы. Гармонический осциллятор – простейшая колебательная механическая система с одной степенью свободы. En=2 p(t)=m(-WAsin(Wt+ 2.Фазовая траектория – это графическое представление динамической системы. Плоскость (р,х) – фазовая плоскость (эллипс).
|
||||||
|
Последнее изменение этой страницы: 2018-04-11; просмотров: 694. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||
 .
.
 ,
,
 ;
; .
. отсюда
отсюда 
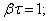




 относительно оси - это проекция на данную ось момента импульса L, определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.
относительно оси - это проекция на данную ось момента импульса L, определенного относительно некоторой точки О, принадлежащей оси, причем, как оказывается, выбор точки О на оси значения не имеет.

 . В этом выражении амплитуда А и начальная фаза j задаются соотношениями
. В этом выражении амплитуда А и начальная фаза j задаются соотношениями 





 =W0t+
=W0t+ 

 уравнение фазовой траектории.
уравнение фазовой траектории. угол поворота [ рад]
угол поворота [ рад] =1 Н*м
=1 Н*м 2)Логарифмический декремент затухания
2)Логарифмический декремент затухания - угловая скорость
- угловая скорость - угловое ускорение
- угловое ускорение ; V=
; V=  =R
=R 
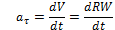 =R
=R 
 =W2R
=W2R ))
)) - уравнение фазовой траектории.
- уравнение фазовой траектории.