Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы расчета электродинамических сил
В нормальном режиме эксплуатации электродинамические усилия невелики. Однако при коротком замыкании в сети по токоведущим частям электрического аппарата протекают токи в десятки раз превышающие номинальные. Эти токи создают ЭДУ, которые могут вызвать деформацию проводников и изоляторов. Под электродинамической устойчивостью электрического аппарата понимается его способность противостоять электродинамическим силам, возникающим при больших токах короткого замыкания.
где IКЗmax – ударный ток КЗ. При расчете электродинамических сил используются два основных метода. Первый метод основан на законе Ампера. Закон Ампера Элементарный проводник
Направление индукции находится по правилу буравчика, а направление силы – по правилу левой руки (рис. 9). Зная направления индукции и силы, а также угол β между векторами
Для определения полной силы F, действующей на проводник длиной l, необходимо просуммировать силы, действующие на все его элементы
В случае любого расположения проводников в одной плоскости β = 900, sinβ = 1, тогда сила определяется по формуле 
Второй метод основан на использовании энергетического баланса системы проводников с током. Сила равна частной производной от электромагнитной энергии W данной системы по координате x, в направлении которой действует сила
Этот метод применяется когда известны аналитические зависимости индуктивностей и взаимоиндуктивностей контуров от их геометрических размеров. Энергия одного контура
Энергия двух контуров с различными токами
где M – взаимная индуктивность контуров. Для одного контура электродинамическая сила будет
Электродинамические силы между параллельными Проводниками.
где Полная индукция от проводника l1 в элементе dx
Элементарная сила на элемент dx будет Полная сила на проводник l2 будет
Обозначим
Коэффициент C зависит от геометрических размеров взаимного расположения проводников (геометрический коэффициент). Рассмотрим частный случай, когда l1 изменяется от –∞ до +∞ , а l2 = l – конечной длины. В этом случае перейдем к новой переменной, выразив переменные через известный параметр a (расстояние между проводниками)
Тогда изменятся пределы интегрирования от π до 0 и получим
Таким образом
Установлено, что в случае l1 = l2 = l и если Если проводники не круглого сечения и нельзя принимать, что весь ток течёт по геометрической оси проводника, то геометрический коэффициент принимается по таблицам, графикам в справочнике (в учебнике). Рассмотрим применение второго метода Пусть оба проводника принадлежат к одной системе, то есть обтекаются одним током (рис. 11).
В соответствии с выражением (33)
зная формулу индуктивности одного контура
при условии, что ток протекает по геометрической оси проводника, при r = 1, получим
Электродинамические усилия возникают не только между двумя параллельными проводниками, но и между перпендикулярными проводниками, в кольцевом витке (рис. 12) и между витками, в проводниках переменного сечения, между проводником и ферромагнитной массой. В контактных системах ЭДУ стараются отключить контакты. Это используется в токоограничивающих автоматах.
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 551. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 В большинстве случаев (для шинопроводов, автоматов и др.) для электрических аппаратов в справочниках указывается ток динамической устойчивости. IДУ – это максимальный ток, который способен выдержать данный аппарат. Многие аппараты подлежат обязательной проверке на динамическую устойчивость
В большинстве случаев (для шинопроводов, автоматов и др.) для электрических аппаратов в справочниках указывается ток динамической устойчивости. IДУ – это максимальный ток, который способен выдержать данный аппарат. Многие аппараты подлежат обязательной проверке на динамическую устойчивость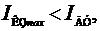
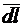 с током i, расположенный в магнитном поле с индукцией
с током i, расположенный в магнитном поле с индукцией 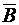 (рис. 8), создаваемой другими проводниками, испытывает силу
(рис. 8), создаваемой другими проводниками, испытывает силу 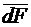 , которая равна
, которая равна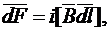 (26)
(26)
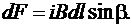 (27)
(27) (28)
(28)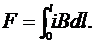 (29)
(29)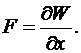 (30)
(30)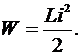 (31)
(31)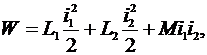 (32)
(32)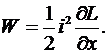 (33)
(33) Согласно закону Био–Саварра–Лапласа элементарная индукция dB от элемента dy и тока i1 в месте расположения элемента dx (рис. 10) равна
Согласно закону Био–Саварра–Лапласа элементарная индукция dB от элемента dy и тока i1 в месте расположения элемента dx (рис. 10) равна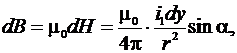 (34)
(34)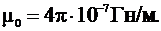 – магнитная проницаемость воздуха, α – угол между током i1 и лучом r.
– магнитная проницаемость воздуха, α – угол между током i1 и лучом r.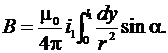 (35)
(35)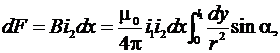 (36)
(36)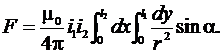 (37)
(37)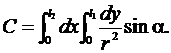 (38)
(38)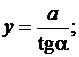
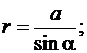
 (39)
(39)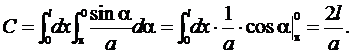 (40)
(40)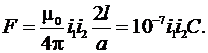 (41)
(41)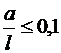 , то
, то 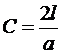 дает погрешность не более 5%.
дает погрешность не более 5%.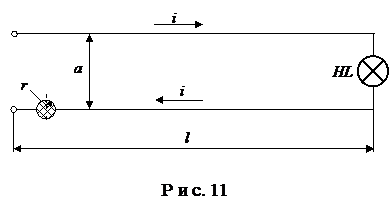
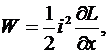
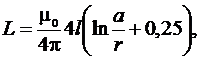 (42)
(42)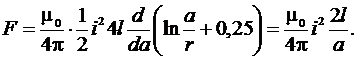 (43)
(43)