Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Инертная и гравитационная массы всех тел строго пропорциональны друг другу. ⇐ ПредыдущаяСтр 2 из 2 Это означает, что при надлежащем выборе единиц измерения гравитационная и инертная массы становятся тождественными, поэтому в физике говорят просто о массе. Тождественность гравитационной и инертной масс положена Эйнштейном в основу общей теории относительности. Отметим, что с самого начала массу полагали совпадающей с инертной массой тел, вследствие чего численное значение g нами было определено в предположении; что те — min. Поэтому (9.8) можно записать в виде
Последнее соотношение позволяет определить массу Земли Мз. Подстановка в него измеренных значений w, Rз и g дает для массы Земли значение 5,98-10 24 кг. Далее, зная радиус земной орбиты Rор и время полного обращения Земли вокруг Солнца Т, можно найти массу Солнца MC. Ускорение Земли, равное cu2#0p (со = 2я/Г), обусловливается силой притяжения Земли к Солнцу. Следовательно,
откуда может быть вычислена масса Солнца. Подобным же образом были определены массы других небесных тел.
Основанием для установления закона всемирного тяготения Ньютону послужили три открытых Кеплером закона движения планет: Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце. 2. Радиус-вектор планеты описывает за равные времена одинаковые площади. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Первый закон Кеплера указывает на то, что планеты движутся в поле центральных сил. Рассмотрим движение частицы в центральном поле сил. Центральная сила имеет вид:
Поскольку эта сила консервативна, то можно ввести потенциальную энергию: 
При движении в центральном поле момент силы равен нулю, т.к. угол между векторами в векторном произведении равен нулю:
Тогда из уравнения моментов получаем, что L есть постоянная величина. При движении частицы в центральном поле полный момент импульса сохраняется несмотря на то, что система (одна частица) не является замкнутой.
рис. 9.4
Так как вектор L = const, т.е. его величина и его направление сохраняются, и вектор L перпендикулярен к векторам rи р, то, следовательно, движение частицы происходит в плоскости перпендикулярной к L . Имеем плоскую орбиту. Если направим ось z по вектору L, то L = Lz и траектория лежит в плоскости, перпендикулярной ocи z. Тогда
Геометрическая интерпретация. Найдем площадь сектора ОАВ (рис. 9.5):
Здесь ОВ - угол между радиусом r = (ОВ) и (АВ) = vdt (в пределе - касательной). Тогда:
рис. 9.5
Введем понятие секториалъной скорости', площадь, описываемая радиусом-вектором за единицу времени:
Таким образом, получаем 2-ой закон Кеплера, гласящий, что секториальная скорость постоянна при движении в центральном поле:
Действительно, траектория тела в поле центральных сил представляет собой плоскую кривую —гиперболу, параболу или эллипс, — фокус которой совпадает с центром сил. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 570. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
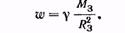 (9.9)
(9.9) (9.10)
(9.10) (9.11)
(9.11)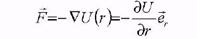 (9.12)
(9.12) (9.13)
(9.13)
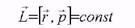
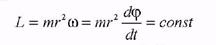 (9.14)
(9.14)


 (9.15)
(9.15)