
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Абсолютная и относительная погрешности вектора.Абсолютная погрешность вектора x* Относительная погрешность вектора x* Выбор той или иной конкретной нормы в практических задачах диктуется тем, какие требования предъявляются к точности решения. Пусть
вычитая из второго уравнения первое, имеем Величину Оценка числа обусловленности. Замечательно, что число обусловленности матрицы совершенно также определяет влияние на погрешности решения возмущения правой части системы. Пусть
Заметим, что если
Здесь Таким образом, чем больше число обусловленности, тем чувствительнее решение линейной системы к погрешностям округления. Системы (матрицы) с большим числом обусловленности называют плохо обусловленными. Реальное вычисление числа обусловленности предполагает знание нормы обратной матрицы, вычисление которой сравнимо по количеству операций с решением системы. Однако для анализа обусловленности системы достаточно знать какую-либо хорошую оценку числа обусловленности, например, часто вычисляется очень точная оценка, нижняя граница истинного числа обусловленности  Решение линейной системы методом Гаусса Методы решения систем линейных алгебраических уравнений можно разделить на точные и приближенные. Примером точных методов может служить метод Крамера, который на самом деле никогда не применяется из-за огромного количества вычислений и связанных с ними ошибок округления. Точные методы решения линейных систем применяют для решения линейных систем относительно небольшой размерности (до
приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей
решение которой находят по формулам Общее число арифметических операций прямого хода метода Гаусса
Пример. Легко убедиться, что точным решением системы является вектор Решение системы линейных алгебраических уравнений методом простых итераций Точные методы решения линейных систем применяют для решения линейных систем относительно небольшой размерности (до Итерационные методы хороши для систем с разреженными матрицами. Разреженными называют матрицы, большинство элементов которых — нули. Рассмотрим простейший итерационный метод решения линейной системы — метод простых итераций. Метод состоит в следующем. Сначала система уравнений
Преобразовать систему Теорема.Пусть выполнено условие Тогда 1) решение 2) при произвольном начальном приближении 1) Из курса линейной алгебры известно, что система линейных алгебраических уравнений имеет единственное решение при любой правой части тогда и только тогда, когда соответствующая однородная система имеет только нулевое решение. Пусть 2) Вычитая из равенства
Вычисляя норму левой и правой частей этого равенства и используя неравенство
Справедливость неравенства (*) установлена. Учитывая, что В качестве условия окончания итерационного процесса можно взять условие Решение системы Метод Зейделя легко записать в компактной матричной форме:
Если
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 227. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
.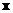 — точное решение линейной системы
— точное решение линейной системы  , а
, а — решение системы с возмущенной матрицей
— решение системы с возмущенной матрицей  :
: ,
,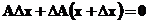 , откуда
, откуда  и, следовательно,
и, следовательно,  .
. принято называть числом обусловленности матрицы.
принято называть числом обусловленности матрицы. :
: ,
,  ,
,  ,
,  и
и  т.е.
т.е. 
 , то
, то  . Такое определение числа обусловленности позволяет дать следующую геометрическую интерпретацию обусловленности матрицы. Матрица
. Такое определение числа обусловленности позволяет дать следующую геометрическую интерпретацию обусловленности матрицы. Матрица 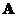 отображает n-мерную единичную сферу (множество векторов единичной длины
отображает n-мерную единичную сферу (множество векторов единичной длины 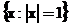 ) в множество векторов различной длины
) в множество векторов различной длины  . Это множество — r-мерный эллипсоид в Rn,r — ранг матрицы А, для невырожденных систем r = n. На рисунке изображен случай n =2.
. Это множество — r-мерный эллипсоид в Rn,r — ранг матрицы А, для невырожденных систем r = n. На рисунке изображен случай n =2.
 и
и 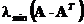 — наибольшее и наименьшее сингулярные числа матрицы — соответственно большая и малая полуоси эллипса и плохая обусловленность отвечает сильно вытянутым эллипсам.
— наибольшее и наименьшее сингулярные числа матрицы — соответственно большая и малая полуоси эллипса и плохая обусловленность отвечает сильно вытянутым эллипсам. , где
, где  — j-й столбец матрицы А,
— j-й столбец матрицы А,  ,
,  ,
,  — специально выбранный вектор, координаты которого
— специально выбранный вектор, координаты которого  .
. ). Метод Гаусса — точный метод решения невырожденной системы линейных алгебраических уравнений. Метод Гаусса, его еще называют методом гауссовых исключений, состоит в том, что систему
). Метод Гаусса — точный метод решения невырожденной системы линейных алгебраических уравнений. Метод Гаусса, его еще называют методом гауссовых исключений, состоит в том, что систему  линейных алгебраических уравнений относительно
линейных алгебраических уравнений относительно 



 , считая размерность системы n.
, считая размерность системы n.
 . Если решить эту задачу методом Гаусса, выполняя вычисления с тремя значащими цифрами, то в результате округлений получится совершенно непригодное решение
. Если решить эту задачу методом Гаусса, выполняя вычисления с тремя значащими цифрами, то в результате округлений получится совершенно непригодное решение  .
. ). Для решения систем большей размерности (
). Для решения систем большей размерности (  ) используют итерационные методы. Для решения систем еще больших размерностей(> 106 ) применяют специальные методы, которые здесь не рассматриваются Метод прогонки – алгоритм решения систем линейных алгебраических уравнений с трехдиагональными матрицами. Общее число арифметических операций прямого хода 8n.
) используют итерационные методы. Для решения систем еще больших размерностей(> 106 ) применяют специальные методы, которые здесь не рассматриваются Метод прогонки – алгоритм решения систем линейных алгебраических уравнений с трехдиагональными матрицами. Общее число арифметических операций прямого хода 8n. преобразуется к виду
преобразуется к виду  и ее решение вычисляется как предел последовательности
и ее решение вычисляется как предел последовательности 
 .
. . Практически это означает, что итерационные последовательности хорошо сходятся для тех матриц, у которых диагональные элементы велики по сравнению с внедиагональными.
. Практически это означает, что итерационные последовательности хорошо сходятся для тех матриц, у которых диагональные элементы велики по сравнению с внедиагональными. системы
системы 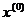 метод простой итерации сходится и справедлива оценка погрешности
метод простой итерации сходится и справедлива оценка погрешности  .(*)
.(*) .
.  . Т.к. по условию
. Т.к. по условию  . Следовательно,
. Следовательно,  равенство
равенство  , получим
, получим .
. получим :
получим :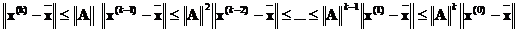 .
. не зависит от k, а
не зависит от k, а  при
при  получаем, что
получаем, что  при
при  , где
, где  — заданная погрешность. Тогда полагаем
— заданная погрешность. Тогда полагаем  .
.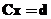 методом Зейделя. В итерационном методе Зейделя (метод Зейделя называют методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений)
методом Зейделя. В итерационном методе Зейделя (метод Зейделя называют методом Гаусса-Зейделя, процессом Либмана, методом последовательных замещений)  . При вычислении каждой последующей компоненты решения используются уточненные значения предыдущих компонент.
. При вычислении каждой последующей компоненты решения используются уточненные значения предыдущих компонент.  ,
,
 ,
,  .
. , то
, то 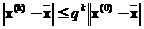 ,
,  . В практических расчетах используют то же условие окончания итерационного процесса, что и в методе простых итераций.
. В практических расчетах используют то же условие окончания итерационного процесса, что и в методе простых итераций.