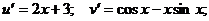Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производная показательно- степенной функции.Стр 1 из 2Следующая ⇒ К У Р С В Ы С Ш Е Й М А Т Е М А Т И К И
Краткий конспект лекций
ЧАСТЬ 2
2001 Дифференциальное исчисление функции Одной переменной. Производная функции, ее геометрический и физический смысл. Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
f(x)
f(x0 +Dx) P Df f(x0) M
a b Dx 0 x0 x0 + Dx x
Пусть f(x) определена на некотором промежутке (a, b). Тогда
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: Уравнение нормали к кривой: Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной. Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.  Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке. Понятно, что это условие не является достаточным.
Основные правила дифференцирования. Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х. 1) (u ± v)¢ = u¢ ± v¢ 2) (u×v)¢ = u×v¢ + u¢×v 3) Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций. 1)С¢ = 0; 9) 2)(xm)¢ = mxm-1; 10) 3) 4) 5) 6) 7) 8)
Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f. Тогда
Доказательство.
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда Теорема доказана.
Логарифмическое дифференцирование.
Рассмотрим функцию Тогда (lnïxï)¢=
Учитывая полученный результат, можно записать Отношение Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных и показательно-степенных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производная показательно- степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной. Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0. Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
Пример. Найти производную функции
По полученной выше формуле получаем: Производные этих функций: Окончательно:
|
||
|
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 176. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
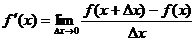
у
тангенс угла наклона секущей МР к графику функции.
,
.
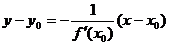при условии, что это отношение существует.
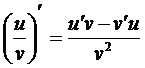, если v ¹ 0
11) 
12) 
13) 
14) 
15) 
16) 
.
, т.к. 
.
.
называется логарифмической производной функции f(x).
.
