Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Таким образом, функция положения реального механизма определяется какXP=XT+DХтехн; где XT – можно рассчитать (расчётные параметры проектируемого механизма); DХтехн = ? В реальном механизме, если считать Dqi – первичной погрешностью, то
Для функции одной переменной её значение в некоторой точке (а) можно представить (определить) в виде ряда Тейлора, т.е.
Если во внимание взять только первые (линейные) два члена разложения ряда Тейлора, то можно записать, что
В общем случае для функции многих переменных ряд Тейлора запишется как
где линейные члены разложения есть частичные систематические погрешности. Тогда по аналогии можно записать
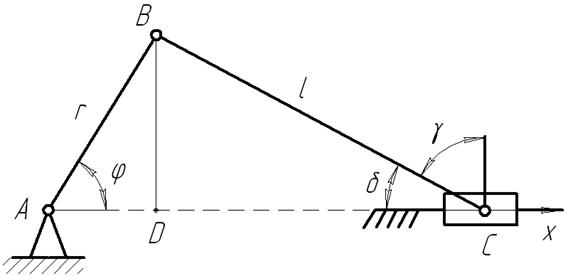
Отсюда следует, что погрешность от одного параметра не оказывает влияния на погрешность от другого параметра, (обеспечивается принцип независимого влияния или так называемый принцип суперпозиции), и общая погрешность определяется алгебраическим сложением частных погрешностей, каждая из которых порождается одной первичной погрешностью. Рассмотрим примераналитического расчёта механизма на точность (рис.2.2.).
Рис. 2.2. Первичные погрешности Dr и D
Для аналитического решения задачи необходимо знание функции положения ведомого звена:
Так как DС=
С учётом этого
где g–угол передачи; d–угол давления. Если g Так как равенство DX=¥ физически невозможно, то получается, что формула не верна? Такое стало возможным только потому, что мы отбросили все нелинейные члены ряда Тейлора. Но из выражения видно, что при увеличении g растёт погрешность положения. Поэтому при проектировании этот угол следует ограничивать. Из анализа полученного выражения также видно, что:  1) при j = 0; 2) при j = 180° Погрешность перемещения будет равна:
Полученные соотношения позволяют сделать вывод, что точность хода (перемещения) ведомого звена кривошипно-ползунного механизма не зависит от точности выполнения шатуна. Добиться повышения точности работы механизма можно, выполнив условие Dr= –Dl, т. е. сделав положение ползуна регулируемым. Подобные расчёты на точность позволяют обоснованно назначать допуски на изготовление деталей и сопряжения, предусматривать некоторые мероприятия по обеспечению работоспособности машины (обеспечивать регулировки). Анализируя метод определения погрешности положения ведомого звена механизма, следует сказать, что для аналитического определения DXj нужно знать Dqi, функцию Xj и частные производные от неё по каждому параметру. Это не всегда возможно, так как зачастую трудно получить как саму функции, так и производные от неё. Графоаналитический метод определения погрешностей с помощью преобразованного механизма. Суть этого метода заключается в определении частных погрешностей механизма построением планов скоростей для некоторого преобразованного механизма. Преобразованный механизм получают закреплением ведущего звена действительного механизма в изучаемом положении, а звено, отображающее погрешность, превращают в ведущее звено другого механизма. При этом направление движения этого звена должно совпадать с направлением изменения параметра (первичной погрешности) исследуемого звена, т. е. практически ведущее звено превращают в стойку и вводят поступательную пару, позволяющую изменять линейный размер (моделировать первичную погрешность). Рассмотрим физический и кинематический смысл производной Ранее было установлено, что DXi есть погрешность положения ведомого звена из-за наличия первичной погрешности Dqi, Тогда погрешность положения для первого звена DX1= Продифференцируем это выражение по времени и получим
где V1K – скорость ведомого звена; V1П – скорость ведущего звена, порождённая первичной погрешностью Dq1, т. е. представляет собой скорость ведущего звена преобразованного механизма из-за изменения длины этого ведущего звена вследствие первичной погрешности. Таким образом, линейное передаточное отношение
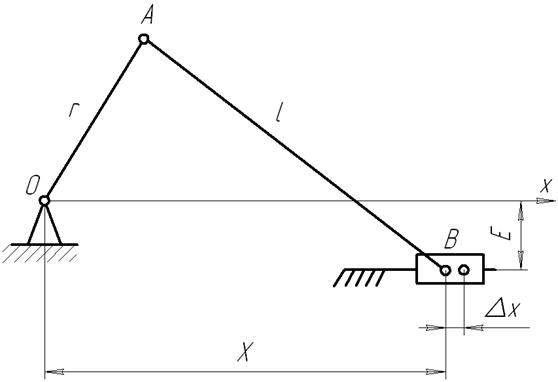
Рассмотрим приложение этого метода на примере кривошипно-ползунного механизма (рис. 2.3).
Рис. 2.3. Строим преобразованный механизм, при котором длина кривошипа вследствие первичной ошибки Dr стала переменной (рис. 2.4). В этом механизме ползуном А воспроизводится погрешность Dr.
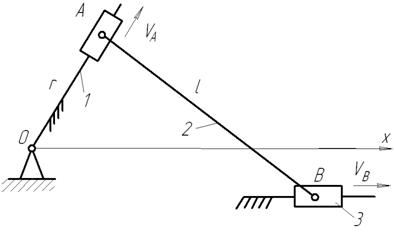
Рис. 2.4. Необходимо построить план малых перемещений, который теоретически построить можно, а практически нет из-за их малости. Но проведенный анализ уже подсказывает методику определения погрешности положения (рис. 2.5).
Рис. 2.5. Перемещение ползуна ~ скорости точек А и В, т.е.
Разделим (2) на (1), получим:
или
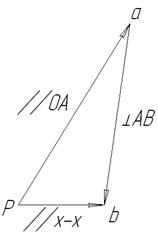
Чтобы найти отношение скоростей, необходимо построить план скоростей (рис. 2.6). Рис. 2.6. Учитывая, что Погрешность положения зависит от первичной погрешности и соотношения скоростей, но не зависит от их номинального значения. Далее строим преобразованный механизм (рис. 2.7), у которого длина шатуна вследствие погрешности стала переменной
Рис. 2.7. Строим преобразованный механизм, при котором величина эксцентриситета вследствие первичной погрешности (величины зазора) стала переменной (рис. 2.8)
Рис. 2.8.
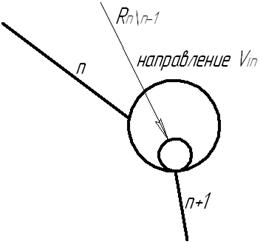
Таким образом, полная погрешность положения ползуна 3 в соответствующем масштабе равна алгебраической сумме частных погрешностей DXT = DX1+DX2+DX3. Или DXтехн = Изложенный метод определения погрешностей применим и для плоских механизмов с высшими кинематическими парами. Однако при этом следует условно заменить высшие пары низшими известным способом (из курса теории механизмов и машин). Таким образом, общая погрешность складывается алгебраически из так называемых частных погрешностей, каждая из которых порождается одной первичной погрешностью (принцип наложения частных погрешностей) DXTехн = Если эти первичные погрешности являются случайными величинами и взаимонезависимыми, то значения их для каждого конкретного случая неизвестны и имеются только вероятностные характеристики, например среднее арифметическое значение параметра D Естественно возникает вопрос, если D Ys = y1×y2×y3,, где Ys – средняя суммарная вероятность. Если y1=y2=y3 и Z=3, тогда Ys=(2,7×10-3)3 » 2×10-8, т. е. вероятность появления трёх максимальных значений равна 2×10-8, т. е. получим 2 совпадения на 1×108 циклов измерения. При Z=2 yi=0,05; Ys=1,25×10-4 – одно совпадение на 104 циклов измерения, т. е. получаем завышенную погрешность положения и, ясно, что в этом случае нельзя суммировать алгебраически максимальные значения частных погрешностей при определении общей погрешности механизма. Теория вероятности в этом случае позволяет определить среднее квадратичное отклонение (s) погрешности положения. Обычно на стадии проектирования математическое ожидание первичной погрешности берут равной половине поля допуска, т. е. Dqi= где ss – среднее квадратическое отклонение суммарной погрешности. Согласно теории вероятности для независимых случайных погрешностей ss= где ds – поле отклонений суммарной средней погрешности. Так как si = ds = 2Zs×ss = 2Zs При Zi=Zs – т. е. при одинаковых законах распределения первичной и суммарной погрешности ds= где ds – среднеквадратичная сумма погрешностей от каждой компоненты. Тогда DXTехн. = При i=2®ds= Таким образом, на стадии проектирования погрешности положения при случайных значениях Dqi, т. е. Dqi¹const; частные случайные погрешности положения складываются геометрически, а не алгебраически, как это при систематических погрешностях. Частные случаи первичных погрешностей и построения преобразованного механизма.При выборе структуры преобразованного механизма обычно применяется ползушка, моделирующая погрешность. В случае определения влияния векторной первичной погрешности, направляющую ползушки располагают вдоль силы давления в данном шарнире, т.е. ползушка должна перемещаться по линии действия давления в кинематической паре (рис. 2.8). Следовательно, при наличии векторной погрешности необходимо предварительно провести силовой расчёт.
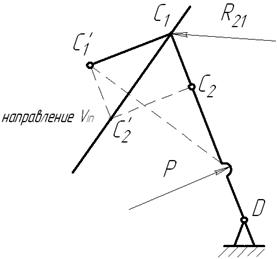
Рис. 2.9. При учёте деформации звеньев направление движения ползушки совпадают с линией, определяющей наибольшую деформацию звена (рис.2.9), где С1 – перемещение точки С вследствие изгиба; С2 – перемещение точки С вследствие погрешности в длине звена. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 364. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
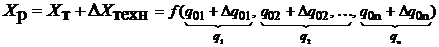
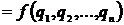
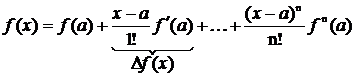 ;
;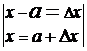 .
.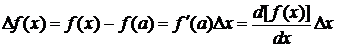 .
.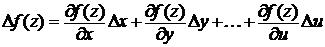 ,
,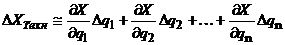
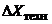
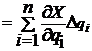 .
.
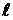 определяют неточность положения ведомого звена, т.е.
определяют неточность положения ведомого звена, т.е.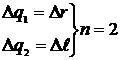
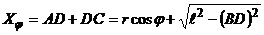 =
= 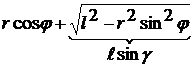 .
.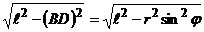 , то
, то
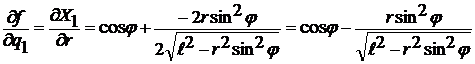
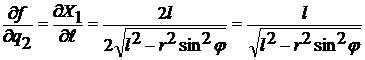 .
.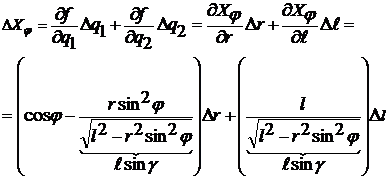
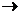 0, то DX
0, то DX 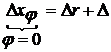 l.
l.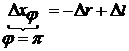
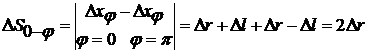
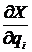 . Эта частная производная представляет собой линейное передаточное отношение, т.е. есть отношение малых перемещений ведомого и ведущего звеньев преобразованного механизма и может быть определена из плана малых перемещений.
. Эта частная производная представляет собой линейное передаточное отношение, т.е. есть отношение малых перемещений ведомого и ведущего звеньев преобразованного механизма и может быть определена из плана малых перемещений.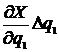 .
.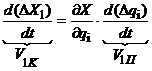 ,
,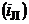 некоторого преобразованного механизма может быть определено как:
некоторого преобразованного механизма может быть определено как: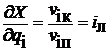 .
.
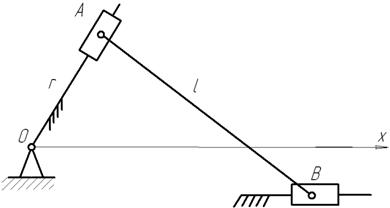
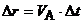 (1)
(1)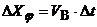 . (2)
. (2)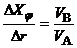
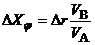 или
или 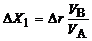
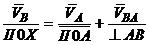
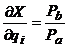 ; DXj = Dr
; DXj = Dr 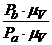 ;
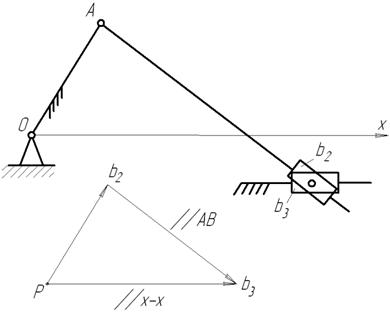
; 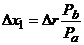 .
.
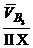
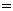
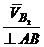 +
+ 
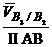 ;
; 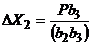
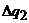 .
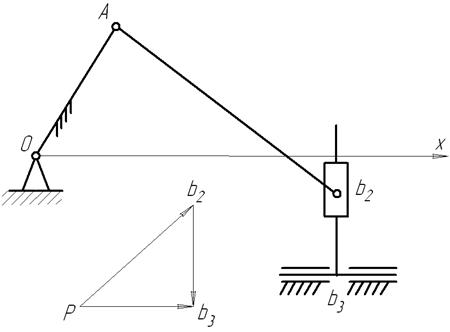
.
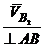 +
+ 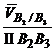 ; DX3 =
; DX3 = 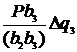 .
.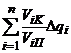
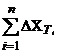
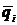 (его математическое ожидание) и si частных погрешностей.
(его математическое ожидание) и si частных погрешностей.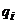 ¹ const (случайна), то какое же брать значение D
¹ const (случайна), то какое же брать значение D 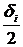 ;
; 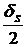 =Zs×ss; ds= 2Z×ss,
=Zs×ss; ds= 2Z×ss,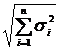 ,
,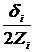 , то
, то 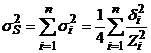 ;
;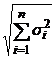 ; ds = Zs
; ds = Zs 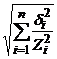 .
.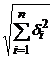 ,
,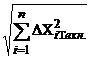 .
.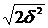 =1,41d; i = 4 ® ds =2d; i = 3 ® ds = 1,73d, а не 3d, как при алгебраическом сложении.
=1,41d; i = 4 ® ds =2d; i = 3 ® ds = 1,73d, а не 3d, как при алгебраическом сложении.