
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Вынужденные колебания. Резонанс.Гармонические колебания. Малые колебания. Затухающие колебания. Вынужденные колебания. Резонанс. Гармонические колебания. Колебаниями, называют такое изменение некоторой физической величины, при котором эта величина, пройдя ряд изменений, возвращается к исходному значению и процесс изменений идёт дальше снова по исходному закону. При гармонических колебаниях интересующая нас физическая величина изменяется по закону: Здесь:
Периодом колебаний отсюда имеем: соответственно, частота (не циклическая) Будем считать, что
Из этих выражений видно, что скорость и ускорение тоже меняются по гармоническому закону с соответствующими изменениями амплитуды и фазы колебаний. Кроме того, из (1) и (6) видно, что  Отсюда видно, что циклическая частота является характеристикой системы (входит в дифференциальное уравнение), а амплитуда и начальная фаза являются константами, определяемыми из начальных условий:
Откуда следует:
Почему гармонические колебания изучаются в качестве отдельного вида движения? Ответ состоит в том, что такие колебания совершает система, находящаяся в положении устойчивого равновесия. Какое положение равновесия называется устойчивым? Очевидно, что положение равновесия считается устойчивым, если потенциальная энергия имеет минимум. Покажем это на случае одномерного движения. Пусть потенциальная энергия дается некоторой функцией здесь мы учли, что в точке минимума первая производная должна быть равна нулю. Выберем начало координат в точке равновесия. В таком случае потенциальная энергия равна: Поскольку потенциальная энергия имеет минимум, то вторая производная должна быть положительной Таким образом, мы показали, что в положении равновесия силы, действующие на частицу, подчиняются закону Юнга, с коэффициентом жесткости В качестве примера рассмотрим груз, который колеблется на пружинке. В этом случае уравнение движения имеет вид:
И с помощью замены Отсюда видно, что потенциальная и кинетическая энергия меняются в противофазе так, что полная энергия остается постоянной. В то же время полная энергия остается постоянной:
Ситуация с трехмерным случаем неустойчивого равновесия оказывается несколько сложней чем одномерный случай, но в конечном счете все сводится к трем малым (гармоническим) независимым колебаниям. Легко также видеть, что средние значения потенциальной и кинетической энергии равны: Затухающие колебания. В реальной ситуации наряду, с силами, удерживающими частицу у положения равновесия и приводящими малым колебаниям всегда существуют неконсервативные силы, которые приводят к потери полной энергии и, в конечном счете, к остановке колебаний. Покажем, как можно учесть «торможение» в случае, когда тормозящими силами являются силы сопротивления среды. При наличии таких сил уравнение движения (14) включает дополнительный член, отвечающий силам сопротивления среды:
которое, после подстановок Если искать решение в виде: То
приходим к уравнению: Если затухание не слишком сильное Если же затухание сильное (
и константы Рассмотрим изменение энергии затухающих колебаний. Очевидно, что из-за наличия диссипативной силы сопротивления среды механическая энергия будет убывать. В качестве конкретного примера рассматриваем груз на пружинке при наличии силы сопротивления среды (уравнения (19), (20)). Затухания считаем малыми
и с учетом слабого затухания получим: после чего энергия системы переписывается в виде:
где Из двух последних формул видно, что энергия затухает в два раза быстрей ( 1. Время релаксации:
Это означает, что зависимость амплитуды от времени можно записать в виде:
такая запись показывает, что за время релаксации амплитуда убывает в
2. Логарифмический декремент затухания.Безразмерная величина, показывающая как быстро затухают колебания за один период:
или с использованием времени релаксации:
где 3. Добро́тность — характеристика колебательной системы, показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. Общая формула для добротности любой колебательной системы:
Вынужденные колебания. Резонанс. Вынужденными колебаниями называются колебания, которые происходят под действием внешней силы, изменяющейся по периодическому закону: Самое общее решение этого уравнения имеет вид:
В теории дифференциальных уравнений первое слагаемое называется общим решением однородного уравнения (уравнения (35) с нулевой правой частью или, что то же, уравнения (20)). Общим это решение называется потому, что оно содержит две произвольные константы (
Подставляя эти производные в (34) имеем:
или
и
Из этих двух уравнений получаем, что: Амплитуда имеет максимальное значение, когда минимально значение подкоренного выражения в знаменателе. Соответствующая частота вынуждающей силы находится из условия:
Соответствующая частота называется резонансной и она равна: При этой частоте амплитуда установившихся колебаний равна: Из этого выражения видно, что при приближении частоты внешней силы к резонансной, амплитуда вынужденных колебаний возрастает, и возрастает тем сильней, чем меньше затухание (см. Рис.1).
Рис.1 Зависимость амплитуды колебаний от частоты вынуждающей силы. Кривая 1 — без затухания
В заключение остановимся на зависимости от времени энергии вынужденных колебаний. Потенциальная и кинетическая и полная энергии равны:
Явление резонанса часто встречается в жизни. Так для того, чтобы не разрушить мост группе солдат проходящих по нему не разрешается идти в ногу. Флаттер, который приводит к разрушению самолёта на определённых частотах, тоже связан резонансом. Да что далеко ходить, когда Вы едите в автобусе и на каких-то участках досаждает дребезжание, а на каких-то нет. Это тоже резонанс.
Ниже приведены некоторые примеры вредных и полезных проявлений резонанса: В 1750 г. близ города Анжера во Франции через цепной мост длиной 102 м шел в ногу отряд солдат. Частота их шага совпала с частотой свободных колебаний моста. В результате резонанса размахи колебаний моста увеличились настолько, что цепи оборвались, и мост вместе с солдатами обрушился в реку; погибло 226 человек.
В 1906 г. по аналогичным причинам обрушился так называемый Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон. Поэтому теперь для предотвращения таких случаев войсковым частям при переходе через мосты приказывают обычно идти не в ногу, а вольным шагом. Поезда же проезжают мосты либо на медленном ходу, чтобы частота ударов колес о стыки рельсов была значительно меньше частоты свободных колебаний моста, либо, наоборот, проносятся через мосты на максимальной скорости.
Однако не следует думать, что резонанс играет только вредную роль и потому с ним всегда нужно бороться. Действие генераторов переменного тока основано на параметрическом резонанасе, возникающем в электрическом колебательном контуре; методы электронного парамагнитного резонанса и ядерного магнитного резонанса - мощные методы исследования строения вещества; используется явление резонанаса и в современных мощных ускорителях - циклотронах; на явлении резонанса основан прибор - частотомер, с его помощью можно измерять частоту колебаний различных систем.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 165. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1)
, (1) — амплитуда колебаний;
— амплитуда колебаний; — фаза колебаний;
— фаза колебаний;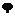 — начальная фаза колебаний;
— начальная фаза колебаний; — циклическая частота колебаний;
— циклическая частота колебаний; называется наименьшее время, после которого система приходит в исходное положение:
называется наименьшее время, после которого система приходит в исходное положение: (2)
(2) (3)
(3) (4)
(4)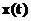 координата материальной точки вдоль оси Х.В таком случае естественно поставить вопрос о том, чему равны скорость и ускорение при гармоническом движении. Вычисляя соответствующие производные, получаем:
координата материальной точки вдоль оси Х.В таком случае естественно поставить вопрос о том, чему равны скорость и ускорение при гармоническом движении. Вычисляя соответствующие производные, получаем: (5)
(5) (6)
(6) (7)
(7) (8a)
(8a) (8b)
(8b) (9a)
(9a) (9b)
(9b) , которая имеет минимум в некоторой точке
, которая имеет минимум в некоторой точке  . Тогда для значений
. Тогда для значений  близких к
близких к  (10)
(10) (11)
(11) . Соответственно сила, действующая на частицу равна:
. Соответственно сила, действующая на частицу равна: (12)
(12) (13)
(13)
 (14)
(14) уравнение приводится к стандартному виду. Мы уже отмечали, что координата скорость и ускорение даются выражениями (1), (5) и (6). Опираясь на это выражение можно написать, как изменяются со временем кинетическая и потенциальная энергии:
уравнение приводится к стандартному виду. Мы уже отмечали, что координата скорость и ускорение даются выражениями (1), (5) и (6). Опираясь на это выражение можно написать, как изменяются со временем кинетическая и потенциальная энергии: (15)
(15) (16)
(16) (17)
(17) (18)
(18)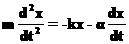 (19)
(19)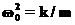 и
и  принимает вид:
принимает вид: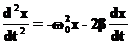 (20)
(20) (20)
(20) (20a)
(20a) (20b)
(20b)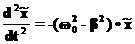 (21)
(21) , то очевидно, что
, то очевидно, что  совершает гармонические колебания с частотой
совершает гармонические колебания с частотой  (т.к. в этом случае.
(т.к. в этом случае.  и
и 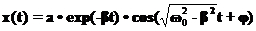 (22)
(22) ), система приходит в положение равновесия не совершая колебаний:
), система приходит в положение равновесия не совершая колебаний: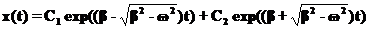 (23)
(23) и
и  определяются из начальных условий.
определяются из начальных условий. . Для расчетов нам понадобится выражение для скорости:
. Для расчетов нам понадобится выражение для скорости: (24)
(24) (25)
(25) (26)
(26) — начальная энергия. Таким образом, при малом затухании можно считать, что система совершает гармонические колебания с амплитудой, которая медленно убывает со временем:
— начальная энергия. Таким образом, при малом затухании можно считать, что система совершает гармонические колебания с амплитудой, которая медленно убывает со временем: (27)
(27)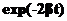 ) чем амплитуда (
) чем амплитуда (  ). Для характеристики затухания пользуются следующими величинами:
). Для характеристики затухания пользуются следующими величинами: (28)
(28) (29)
(29) раз (в 2.7182818284590452 раза) :
раз (в 2.7182818284590452 раза) : (30)
(30) (31)
(31) (32)
(32) — число колебаний которое успевает совершить система пока амплитуда уменьшится в
— число колебаний которое успевает совершить система пока амплитуда уменьшится в  (33)
(33) (34)
(34) (35)
(35) и
и  (36)
(36) (37)
(37) (38)
(38)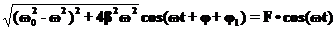 (39)
(39) (40)
(40) (21)
(21) (22)
(22) (23)
(23) (24)
(24)
 , кривые 2,3,4 отвечаю все более сильному затуханию (
, кривые 2,3,4 отвечаю все более сильному затуханию (  ). Амплитуда вынуждающей силы
). Амплитуда вынуждающей силы  для всех кривых одинакова.
для всех кривых одинакова. (25)
(25)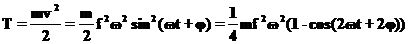 (26)
(26) (27)
(27)