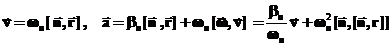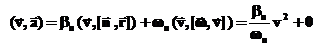Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторы. Радиус-вектор. Скалярное и векторное произведение. Кинематика материальной точки. Поступательное и вращательное движение.Кинематика. При описании движения будем разделять следующие случаи:
Зададим себе вопрос. Что значит описать движение тела? Очевидно, что для этого достаточно описать движение каждой точки тела. И еще один вопрос, Всегда ли необходимо описывать движение тела? А вот ответ на этот вопрос зависит от того, что вы хотите описать. Когда Вам досаждает комар, то достаточно описать (проследить, предугадать) куда он прилетит. А вот когда специалист по изучению насекомых следит за комаром, то ему может оказаться нужным проследить, как он работает крыльями (может ли он лететь вниз головой и т.п.). Отсюда совет: «в профессиональной деятельности не жалейте времени на обдумывание постановки и методов решения. Может быть жизнь вам докажет, что это так. Кстати при поступательном движении твердого тела (что это такое узнаете очень скоро) достаточно описать движение какой-то его одной точки. Итак, одним из основных понятий в динамике является понятие материальной точки. Как видно из названия это почти математическая точка, т.е. объект, который не имеет размеров, а только положение. А материальная она потому, что ещё и имеет массу. Для кинематики это не важно, но для динамики без массы, как вы увидите, не обойтись. А теперь коротко вспомним то, что вы проходили в школе. Пусть наша точка движется вдоль прямой линии. Средней скоростью будем называть пройденный путь, 
Что можно сказать, глядя на это выражение:
Т.е. средняя скорость недостаточно детально описывает характер движения точки. Для того чтобы детализировать описание движения возьмем два значения времени Тогда путь, пройденный за указанный промежуток времени, равен
Вспоминая определение производной можно сказать, что скорость равна производной от пути по времени. Для производной по времени используют следующие обозначения:
Не задумывайтесь над последним обозначением, принимайте его просто как обозначение и нечего больше. Маленькая разминка. Если зависимость пройденного пути от времени дается выражением:
В этом случае скорость равна:
Производная по времени от скорости показывает, как быстро изменяется скорость и называется ускорением (хотя конечно бывают случая, когда оно никакое не ускорение, а замедление). В рассматриваемом примере ускорение равно:
Итак, мы ввели понятие мгновенной скорости, однако пока она не показывает, в какую сторону движется частица. Т.е., зная пройденный путь мы не можем, вообще говоря, сказать, где в тот или иной момент времени находится частица. Для полного описания одномерного движения введем координатную ось. Тогда положение материальной точки в каждый момент времени дается координатой
Очевидно, что ускорение дается аналогичным выражением:
Последнее выражение показывает, как мы будем обозначать вторую производную. Из приведенных выражений следует:
Перейдем к описанию трехмерного движения. В этой части предполагается, что вы хорошо знаете свойства векторов. Необходимо знать, как складывать вектора, как их умножать на число, знать понятие базиса, скалярного и векторного произведений. Для описания положения точки в общем случае будем использовать понятие радиус-вектора. Радиус-вектором называется вектор, проведенный из начала координат в положение, где находится точка. Если положение точки меняется, то меняется и радиус вектор. Геометрическое место концов радиус-вектора называется траекторией. Несколько слов об обозначениях:
Разложение радиус вектора по координатам имеет вид:
Модуль радиус вектора равен:
Обобщая наш одномерный случай на трехмерное движение, получаем выражение для скорости:
А для ускорения имеем:
Итак, подведем итог — радиус вектор, скорость и ускорение являются векторами. В нашем случае это трехмерные вектора. Т.е. вектор — это три числа, точнее три функции времени. Путаница, которая может возникнуть с непониманием понятия модуля вектора, иллюстрируется на следующем примере. Модуль приращение радиус вектора за интервал времени от
А приращение модуля равно:
Это совсем не одно и то же: Больше того, можно привести пример (приведите), когда
Таким образом, можно сказать, что модуль скорости говорит о том, как быстро наша точка движется, а компоненты скорости говорят как быстро точка движется по направлению соответствующей оси, и в каком направлении вдоль этой оси. Понятие радиус-вектора и скорости иллюстрируются на Рис.1.
Ускорение показывает, во-первых, как меняется скорость по величине (как меняется модуль скорости) и, во-вторых, как меняется скорость по направлению. Поэтому ускорение иногда разделяют на две составляющие (см. Рис. 2):
1. Тангенциальное ускорение (обозначают
При этом легко видеть, что:
То, что эта величина показывает, как быстро изменяется величина скорости можно увидеть из следующей цепочки формул:
2. Нормальное ускорение (обозначают
Рассмотрим два примера. В первом частица движется по закону:
При этом
В этом случае, очевидно, что тангенциальное и нормальные ускорения равны:
Ответ понятен, поскольку это движение вдоль прямой линии. Никуда-то наша частица с этой линии не сворачивает, и нет у неё нормального ускорения. Ещё один пример:
Скорость и ускорение равны:
Откуда получаем:
Да это и не удивительно, поскольку частица в этом примере движется по окружности радиуса
А величина скорости и ускорения равны:
Остановимся коротко на двух видах движения твердого тела (термин твердое тело в этом курсе называется недеформируемое тело). Поэтому будем пользоваться следующим определением: Твердое тело— это тело расстояние между любыми точками которого остается постоянным. Выше было сказано, что существует такой вид движения твердого тела, при котором для полного описания движения тела достаточно знать закон движения, какой-нибудь точки этого тела. Такое движение называется поступательным. По определению: Поступательным движением— называется такое движение, при котором линия, соединяющая любые две точки, остается параллельной сама себе. На Рис. 3 показано как это выглядит.
Из определения следует, что если известен закон движения точки A, то закон движения точки B имеет вид:
Произвольное движение твердого тела можно представить как сумму поступательного движения и вращения вокруг некоторой оси, которая, вообще говоря, меняет свое положение в пространстве во время движения. В данном курсе, мы остановимся толькона одном виде вращательного движения — вращение вокруг неподвижной оси(см. Рис.4)..
В этом случае траектория каждой точки тела является окружностью с центром на оси вращения. Поэтому остановимся на описании движения некоторой точки тела. Пусть тело за промежуток времени
Введем вектор
По определению скорости получим:
Кстати, если ввести расстояние до оси вращения, то величина скорости оказывается связанной с расстоянием до оси вращения выражением известным из школьного курса физики:
где Мы ввели обозначение угловой скорости
Аналогично вводится и угловое ускорение:
В таком случае для ускорения получаем:
Попробуем ответить на вопрос, какое слагаемое соответствует тангенциальному ускорению, а какое нормальному. Для этого воспользуемся формулами (17) и (20). В таком случае для тангенциального уравнения имеем:
Т.е. за тангенциальное ускорение (изменение модуля скорости) отвечает только угловое ускорение. Пойдем дальше, будем рассматривать только случай, когда ось вращения не меняет своего положения в пространстве. При этом и угловая скорость и угловое ускорение всегда направлены вдоль оси вращения. Тогда мы можем написать:
где В этом случае:
Это означает, что первое слагаемое отвечает тангенциальному ускорению, а второе нормальному, так как:
Еще интересно заметить, что нормальное ускорение всегда направлено к оси вращения и лежит в плоскости перпендикулярной к оси вращения. Поэтому это ускорение называется центростремительным. Итак, мы познакомились со следующими понятиями: 1. Материальная точка 2. Радиус-вектор 3. Скорость (мгновенная скорость, средняя скорость) 4. Ускорение (нормальное и тангенциальное) 5. Траектория — геометрическое место точек концов радиус вектора 6. Твердое тело (недеформируемое тело) 7. Поступательное движение твердого тела 8. Вращательное движение твердого тела (вокруг фиксированной оси) 8.1.1. Угловая скорость 8.1.2. Угловое ускорение 8.1.3. Центростремительное ускорение
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 226. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
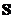 делённый на интервал времени, в течение которого этот путь был пройден:
делённый на интервал времени, в течение которого этот путь был пройден:
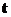 и
и 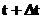 .
.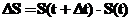 . Ну а если уменьшать время
. Ну а если уменьшать время 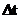 , то в пределе получим мгновенную скорость (часто слово мгновенная опускают и говорят просто скорость):
, то в пределе получим мгновенную скорость (часто слово мгновенная опускают и говорят просто скорость):
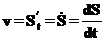
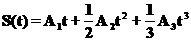
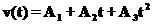
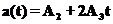
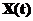 . В этом случае вводят проекцию скорости на ось
. В этом случае вводят проекцию скорости на ось 
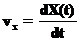
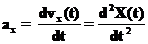
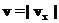
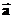
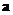 , либо
, либо 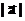 .
.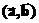 , либо
, либо 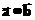 .
.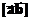 , либо
, либо 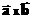 .
.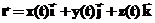
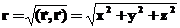
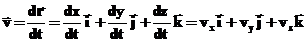
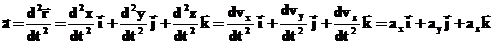
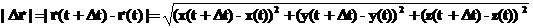
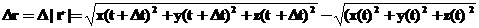
 , а
, а  . И еще некоторые замечания о кинематических соотношениях: Легко видеть, что
. И еще некоторые замечания о кинематических соотношениях: Легко видеть, что 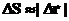 и тем точнее, чем меньше
и тем точнее, чем меньше 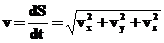
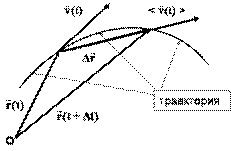 Рис. 1
Рис. 1
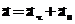

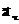 )— проекция ускорения на направление скорости. Тангенциальное ускорение показывает, как меняется величина (модуль) скорости. Если известно полное ускорение
)— проекция ускорения на направление скорости. Тангенциальное ускорение показывает, как меняется величина (модуль) скорости. Если известно полное ускорение 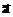 и скорость
и скорость 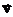 , то это ускорение можно вычислить по формуле:
, то это ускорение можно вычислить по формуле: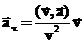
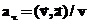
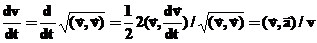
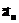 )— проекция ускорения на направление перпендикулярное скорости. Очевидно, что это ускорение показывает, насколько быстро меняется направление скорости. Из формул (16) и (17) следует, что:
)— проекция ускорения на направление перпендикулярное скорости. Очевидно, что это ускорение показывает, насколько быстро меняется направление скорости. Из формул (16) и (17) следует, что: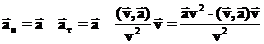
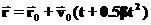
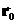 ,
, 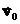 и
и 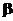 — константы. Тогда скорость и ускорение соответственно равны:
— константы. Тогда скорость и ускорение соответственно равны: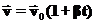
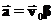
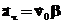
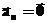
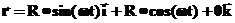
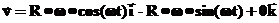
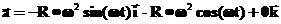
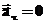
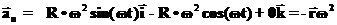
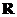 с центром в начале координат:
с центром в начале координат: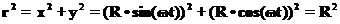
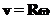
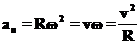


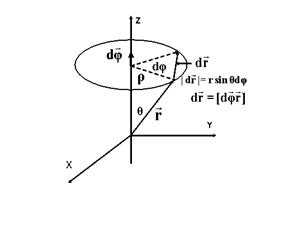
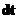 совершило бесконечно малый поворот на угол
совершило бесконечно малый поворот на угол 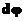 . Как видно из рисунка линейное перемещение радиус вектора рассматриваемой точки связано с углом поворота соотношением:
. Как видно из рисунка линейное перемещение радиус вектора рассматриваемой точки связано с углом поворота соотношением: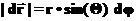
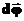 , направленный вдоль оси вращения и имеющий длину
, направленный вдоль оси вращения и имеющий длину 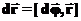
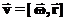
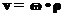 ,
,
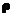 — радиус окружности (расстояние до оси) по которой вращается точка.
— радиус окружности (расстояние до оси) по которой вращается точка. :
: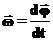
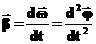
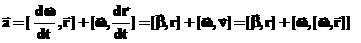
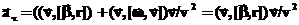
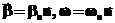 ,
,
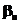 и
и  — проекция углового ускорения и угловой скорости на ось вращения.
— проекция углового ускорения и угловой скорости на ось вращения.