
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Единицы измерений. Система единиц СИ. Размерности величин. Анализ размерностейИзмерения. Погрешности измерений. Измерения. Прямые и косвенные измерения. Случайные и систематические погрешности измерений. Распределение Гаусса. Единицы измерений. Система единиц СИ. Размерности величин. Анализ размерностей Физика наука экспериментальная. Это означает, что все физические законы должны подтверждаться экспериментальными данными, т. е. измерениями. Больше того, очень часто, но не всегда, физические законы начинаются с экспериментальных данных. Иногда какой-либо закон (эффект, явление) предсказывается до эксперимента. Тогда ставится эксперимент, который и проверяет истинность предложенного (открытого) закона. Итак, поговорим об измерениях. Очевидно, что любая величина измеряется с какой-то точностью. Причины: 1. точность прибора (цена деления термометра, цена деления линейки и т.п.); 2. ошибки, связанные с методом измерения (не всегда можно приложить эталон, иногда процесс измерения выглядит достаточно сложно); 3. иногда возникают ошибки, которые трудно учесть, но они откуда-то возникают. Такие ошибки называют систематическими. Это может быть нестабильность каких-то параметров, которые в данном измерении не контролируются (температура, влажность, да мало ли что). Но только ошибки оказываются больше, чем можно ожидать. Остановимся кратко на классификации ошибок измерений, или как их еще называют погрешностей измерений. Абсолютной погрешностью измерений называется разность между измеренным значением физической величины и ее точным значением: 
Здесь введены обозначения Как записывают абсолютную ошибку, да очень просто: Думаю, что в такой записи все понятно. Обратите внимание, что даже если измеренная величина равна . Ясно, что измерить расстояние от Дубны до Москвы Не всегда интересующую нас физическую величину можно померить имеющимися приборами. Иногда эта величина задана какой-то функцией от других величин, которые мы знаем с какими-то погрешностями. Например, нас интересует средняя скорость,
А время и путь известны с какими-то абсолютными погрешностями Пусть какая-то величина А результаты измерений независимых переменных известны и могут быть записаны в виде. В таком случае за измеренное значение величины Ответ кажется естественным. А ошибка (абсолютная погрешность) этой величины дается следующим выражением: И окончательно имеем а частные производные равны: И согласно (10) находим, что абсолютная ошибка средней скорости равна: Итак, по способу получения интересующей нас величины измерения делятся на два вида: 1. Прямые измерения— измерения, при которых интересующая величина получается непосредственно в процессе измерения (по прибору, линейке и т.п.). 2. Косвенные измерения— измерения, при которых интересующая величина рассчитывается по формуле (является функцией величин полученных при прямых измерениях). Есть два вида представления погрешностей измерений: Абсолютная погрешность (абсолютная ошибка) — величина показывающая насколько истинное значение отличается от точного. Абсолютная ошибка имеет ту же размерность, что и измеряемая величина (метры, секунды, …). Относительная ошибка— показывает во сколько раз ошибка меньше измеряемой величины. Относительная ошибка величина безразмерная и часто выражается в процентах. На этом закончим с ошибками измерений. Результатами этой части лекции Вам придется пользоваться при обработке результатов измерений полученных при выполнении лабораторных работ. Погрешности физических измерений принято подразделять на систематические, случайные и грубые: 1. Систематические погрешности вызываются факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Систематические погрешности скрыты в неточности самого инструмента и неучтенных факторах при разработке метода измерений. Обычно величина систематической погрешности прибора указывается в его техническом паспорте. Что же касается метода измерений, то здесь все зависит от квалификации экспериментатора. Хотя суммарная систематическая погрешность во всех измерениях, проводимых в рамках данного эксперимента, будет приводить всегда либо к увеличению, либо к уменьшению правильного результата, знак этой погрешности неизвестен. Поэтому на эту погрешность нельзя внести поправку, а приходится приписывать эту погрешность окончательному результату измерений. 2. Случайные погрешностиобязаны своим происхождением ряду причин, действие которых неодинаково в каждом опыте и не может быть учтено. Они имеют различные значения даже для измерений, выполненных одинаковым образом, то есть носят случайный характер. Допустим, что сделано n повторных измерений одной и той же величины. Если они выполнены одним и тем же методом, в одинаковых условиях и с одинаковой степенью тщательности, то такие измерения называются равноточными. 3. Грубые погрешностиили промахи. Под грубой погрешностью измерения, понимается погрешность, существенно превышающая ожидаемую при данной процедуре измерений. Она может быть сделана вследствие неправильного применения прибора, неверной записи показаний прибора, ошибочно прочитанного отсчета и т.п. Обычно грубые погрешности просто не учитываются при дальнейшей обработке. Остановимся немного подробнее на процессе измерений некоторой величины (кстати, то о чем будет говориться ниже применимо не только к измерениям в физике, но и к измерениям вообще). Если какая-то величина 1. Какое значение следует приписать измеряемой величине? Как оно связано с полученными при измерениях значениями 2. Что можно в этом случае сказать о точности измерений? 3. Что в этом случае понимать под точностью измерений? Можно ли увеличивая число измерений улучшить точность? Для получения ответа на этот вопрос сделаем предположение, что разные значения измеренной величины получаются из-за того, что на процесс измерения влияет случайные факторы, которые учесть невозможно. Например, при взвешивании очень легкого предмета не учитывается движение автомобилей рядом с лабораторией, потоки воздуха в самой лаборатории и т.п. В таких условиях измеряемая физическая величина принимает случайное значение. Внимание — случайное совсем не означает произвольное. В теории вероятностей для описания непрерывной случайной величины Отметим некоторые свойства плотности вероятности, с которыми Вы столкнетесь при изучении теории вероятностей, и которые представляются очевидными: 1. Плотность вероятности не может быть отрицательной 2. Поскольку случайная величина должна принимать хоть какое-нибудь значение то интеграл от плотности вероятности по всем значениям случайной величины должен быть равен единице. Это равенство называется условием нормировки. 3.Наконец можно отметить, что вероятность попадания случайной величины в интервал [x, x+dx] для достаточно малых dxдается следующим выражением:
В теории вероятностей Вы узнаете, что за измеренную величину необходимо принимать арифметическое среднее по всем измерениям: В физике обычно, среднюю величину обозначают либо заключенной в угловые скобки, либо с чертой сверху. Если при этом каждое измерение отличается одно от другого (т.е. разброс в измерениях больше шкалы прибора), то тогда ошибка в такой серии измерений вычисляется по формуле: Из теории вероятностей вы узнаете, что выражение, которое стоит под корнем, называют несмещенной оценкой квадрата дисперсии. Еще раз подчеркнем, что считать ошибку по приведенной формуле нужно, если разброс измерений больше чем цена деления прибора. Если же во всех измерениях вы получаете одно и то же значение, то за абсолютную ошибку следует принять цену одного деления (последнюю из значащих цифр, которую ваш вольтметр, секундомер и т.п. показывает). Ещё несколько коротких замечаний, суть которых Вы поймете подробнее при изучении теории вероятностей. Очевидно, что измеряемая нами физическая величина принимает случайное значение. Внимание — случайное совсем не означает произвольное. В тории вероятностей для описания непрерывной случайной величины При правильно организованном процессе измерения распределение измеряемых значений подчиняется распределению Гаусса. В математике такое распределение чаще называется нормальным распределением. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что правильно подготовленный процесс измерений как раз и подчиняется этим условиям, Распределение Гаусса (нормальное распределение) имеет вид: Нормальное распределение зависит от двух параметров — смещения (среднего значения
И еще одно замечание о распределении Гаусса. Вероятности того, что измеряемая величина окажется в некоторых интервалах, приведены в таблице 1.
Вообще обработка результатов измерений является довольно основательной работой. Мы же на этом закончим, договорившись, что будем принимать, что абсолютная ошибка, о которой речь шла выше, равна дисперсии. Так если, например, при измерении какого-то расстояния мы получили результат Таким образом, запись результата измерений, которая дается формулой (3) означает, только то, что с определённой вероятность значение измеренной величины лежит в определенном интервале. И эта вероятность определяется нормальным распределением с дисперсией
|
|||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 282. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) — для измеренного значения величины
— для измеренного значения величины  , и
, и  — для ее точного значения. Обратите внимание, что абсолютная погрешность измеряется в каких-то величинах. Так если вы меряете время — то величина абсолютной ошибки может измеряться в секундах, или в часах или в минутах или …. В чем захотим, в том и померяем, но главное чтобы то в чем меряем, было для измерения времени, а не длины или площади или веса или еще чего-нибудь. То в чем меряется величина — называется размерностью величины, и об этом мы еще сегодня поговорим. У любого измерения всегда есть ошибка. Хотя бы потому, что ваш измерительный прибор (например, просто линейка) имеет конечную цену деления. В этом случае, за ошибку принимают цену деления, или половину цены деления.
— для ее точного значения. Обратите внимание, что абсолютная погрешность измеряется в каких-то величинах. Так если вы меряете время — то величина абсолютной ошибки может измеряться в секундах, или в часах или в минутах или …. В чем захотим, в том и померяем, но главное чтобы то в чем меряем, было для измерения времени, а не длины или площади или веса или еще чего-нибудь. То в чем меряется величина — называется размерностью величины, и об этом мы еще сегодня поговорим. У любого измерения всегда есть ошибка. Хотя бы потому, что ваш измерительный прибор (например, просто линейка) имеет конечную цену деления. В этом случае, за ошибку принимают цену деления, или половину цены деления.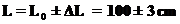 (2)
(2) , то пишут
, то пишут  , т.е. последняя оставленная цифра имеет тот же порядок, что и ошибка. Следующие знаки оставлять бессмысленно, поскольку ошибка больше чем величина отбрасываемого при округлении остатка. В нашем примере говорят, что величина
, т.е. последняя оставленная цифра имеет тот же порядок, что и ошибка. Следующие знаки оставлять бессмысленно, поскольку ошибка больше чем величина отбрасываемого при округлении остатка. В нашем примере говорят, что величина  измерена с точностью 3 смили по другому, абсолютная погрешность
измерена с точностью 3 смили по другому, абсолютная погрешность  (13)
(13) с абсолютной ошибкой
с абсолютной ошибкой  намного сложнее, чем рост баскетболиста
намного сложнее, чем рост баскетболиста  с той же точностью с той же абсолютной ошибкой
с той же точностью с той же абсолютной ошибкой  . И это видно на примере относительных ошибок: в первом случае
. И это видно на примере относительных ошибок: в первом случае  , а во втором
, а во втором  . Когда относительная ошибка не очень большая, то ее обычно выражают в процентах.
. Когда относительная ошибка не очень большая, то ее обычно выражают в процентах. (6)
(6) . Спрашивается чему в таком в таком случае равно среднее значение скорости и её погрешность? Ответ дает следующее правило:
. Спрашивается чему в таком в таком случае равно среднее значение скорости и её погрешность? Ответ дает следующее правило: является функцией от N независимых переменных
является функцией от N независимых переменных 
 (7)
(7) (8)
(8) (9)
(9) (10)
(10) , где измеренное значение и ошибка даются выражениями (9) и (10). Здесь мы воспользовались стандартным обозначением для частных производных. Проведем эту процедуру для средней скорости (6)
, где измеренное значение и ошибка даются выражениями (9) и (10). Здесь мы воспользовались стандартным обозначением для частных производных. Проведем эту процедуру для средней скорости (6) (11)
(11) (12)
(12) (13)
(13)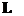 измерялась несколько раз (Nраз). Таким образом, мы получаем N значений измеряемой величины. При этом возникают следующие вопросы:
измерялась несколько раз (Nраз). Таким образом, мы получаем N значений измеряемой величины. При этом возникают следующие вопросы: ?
? вводят плотность вероятности . Плотность вероятности дает ответ на вопрос: «С какой вероятностью величина x попадает в интервал
вводят плотность вероятности . Плотность вероятности дает ответ на вопрос: «С какой вероятностью величина x попадает в интервал  :
: (14)
(14)
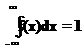 (15)
(15) (16)
(16) (17)
(17)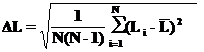 (18)
(18) (19)
(19) ) и масштаба (дисперсии
) и масштаба (дисперсии  ). В случае измерений
). В случае измерений  Рис. 1
Рис. 1




 , то согласно таблице с вероятность чуть больше половины (а точнее 0.6826) измеряемая величина лежит в интервале
, то согласно таблице с вероятность чуть больше половины (а точнее 0.6826) измеряемая величина лежит в интервале  . И наверняка (с вероятностью 0.9973) измеряемая величина лежит в интервале
. И наверняка (с вероятностью 0.9973) измеряемая величина лежит в интервале  .
. и средним значением
и средним значением  .
.