
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема о циркуляции вектора магнитной индукции.Движение заряженных частиц в электрических и магнитных полях. Теорема о циркуляции вектора магнитной индукции.
При движении в статическом электрическом поле сохраняется энергия. Это позволяет написать связь между скоростью (модулем скорости) в различные моменты времени: Для детального описания необходимо решать уравнение движения исходя из второго закона Ньютона и известных сил. Самым простым случаем является постоянное электрическое поле, в котором частица движется с постоянным ускорением: А траектория в этом случае имеет вид: В случае постоянного магнитного поля частица движется по винтовой линии. Шаг винтовой линии зависит от компоненты начальной скорости направленной параллельно магнитному полю, а радиус окружности, описываемой траекторией в плоскости перпендикулярной магнитному полю определяется составляющей скорости перпендикулярной магнитному полю, величиной магнитного поля, зарядом и массой частицы. Получим этот результат исходя из уравнений движения. Направим ось Z вдоль магнитного поля, которое предполагается постоянным. Тогда уравнения движения имеют вид: Отсюда видно, что вдоль магнитного поля частица движется без ускорения и уравнение движения вдоль оси магнитного не зависит от движения вдоль других осей. Таким образом:  Остановимся несколько подробнее на движении в плоскости перпендикулярной магнитному полю. Удобно остановиться на уравнениях для скоростей: Из этой системы дифференциальных уравнений легко получить, что При изучении малых колебаний мы уже получили, что такому уравнению отвечают гармонические колебания с циклической частотой:
Из первого уравнения системы (6) имеем: В соответствии с (5), (8) и (9) закон движения имеет вид: Из (8) и (9) видно, что ось X выбрана вдоль проекции скорости Таким образом, в постоянном магнитном поле заряженная частица движется по винтовой линии с радиусом, который зависит как от величины поля, так и от проекции скорости на плоскость перпендикулярную направлению поля.
Теорема о циркуляции вектора магнитной индукции.
Вычислим для бесконечного проводника с током интеграл по контуру, показанному
Рис.1 на Рис.1 (по круговому контуру который обходится по часовой стрелке). Поскольку Опираясь на эти выражения, интеграл по контуру легко вычисляется: Этот пример является иллюстрацией частного случая общей теоремы, (не будем её доказывать) которая говорит, что: «Интеграл по замкнутому контуру от вектора магнитной индукции равен произведению магнитной постоянной В последнем равенстве учтено, что ток равен интегралу от плотности тока по поверхности. Для задач, обладающих симметрией, теорема о циркуляции вектора магнитной индукции играет ту же роль, что теорема Гаусса для вектора напряженности электрического поля. В качестве примера применения этой теоремы рассмотрим вопрос о нахождении индукции магнитного поля для проводника радиуса ` поля вне проводника имеем `
Чтобы записать теорему о циркуляции в дифференциальном виде воспользуемся теоремой Стокса: где интеграл берется по поверхности опирающейся на контур, а операция вычисления ротора С использованием теоремы Стокса теорема о циркуляции магнитного поля (15) может быть переписана в виде: Отсюда, в силу произвольности контура интегрирования эта теорема может быть переписана в дифференциальном виде: Кстати, из равенства нулю циркуляции статического электрического поля следует, что его ротор равен нулю:
|
|||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 160. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7) . Выберем решение в виде:
. Выберем решение в виде: (8)
(8) (9)
(9) (10)
(10) в нулевой момент времени на плоскость перпендикулярную полю. Легко видеть, что траектория в плоскости перпендикулярной к направлению поля является окружностью с центром в точке
в нулевой момент времени на плоскость перпендикулярную полю. Легко видеть, что траектория в плоскости перпендикулярной к направлению поля является окружностью с центром в точке  и радиусом
и радиусом  . Это следует из очевидного равенства:
. Это следует из очевидного равенства: (12)
(12)
 и
и 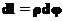 , а величину поля мы вычисляли раньше и получили:
, а величину поля мы вычисляли раньше и получили: (13)
(13) (14)
(14) на алгебраическую сумму токов охватываемых контуром»
на алгебраическую сумму токов охватываемых контуром» (15)
(15) по которому течет ток с постоянной плотностью
по которому течет ток с постоянной плотностью  . Для кругового контура, проходящего внутри проводника, имеем:
. Для кругового контура, проходящего внутри проводника, имеем: (16a)
(16a) (16b)
(16b)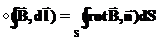 (17)
(17) ставит в соответствие векторной функции (векторному полю) другую векторную функцию, вычисляемую по следующему правилу:
ставит в соответствие векторной функции (векторному полю) другую векторную функцию, вычисляемую по следующему правилу: (18)
(18)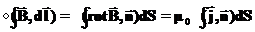 (19)
(19) (20)
(20) (21)
(21)