
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
На сьогоднішній день відомо 46 простих чисел Мерсенна.Лабораторна роботи №3 Тема: «Встановлення належності заданого елементадопідмножининатурального ряду»
Львів 2017 Загальні вказівки до виконання лабораторних робіт Дані методичні вказівки містять опис і порядок виконання лабораторних робіт з дисципліни «Дискретна математика». Метою лабораторних робіт є дослідження методів і алгоритмів побудови і ослідження множин в автоматизованих системах управління. Про готовність до роботи свідчать знання змісту роботи й основних теоретичних положень, розглянутих у роботі. Звіти про виконану роботу повинні бути складені технічно грамотно й закінчуватися самостійними висновками, оскільки студент повинен творчо підходити до отриманих результатів роботи, використовуючи свої практичні навички й теоретичні знання. Лабораторні роботи повинні бути оформлені у вигляді звіту із вказівкою прізвища, ініціалів і групи студента. Перед захистом по лабораторних роботах студент повинен подати оформлений звіт на перевірку викладачеві.
Лабораторна робота №3 Тема роботи:Встановлення належності заданого елемента до підмножини натурального ряду. Мета роботи:Навчитись знаходити і аналітично відображати закономірності розміщення елемента в підмножині натурального ряду. Короткітеоретичнівідомості Додатні числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ..., що з’явилися в результаті рахунку називаються натуральними і утворюють натуральний ряд чисел. Для запису натуральних чисел користуються десятковою системою числення, в основі якої лежать десять знаків - цифр. На першому місці в натуральному ряді стоїть число 1, за ним іде число 2, далі 3 і так до 9. Після 9, згідно з правилом десяткового числення, йде число 10, а за 10 іде 11, і у натуральному ряді немає останнього числа - за кожним натуральним числом стоїть ще одне натуральне число, за яким - ще одне і т.д.  Натуральних чисел нескінченно багато. Найбільше натуральне число назвати в принципі неможливо, оскільки нескінченність ряду таких чисел розуміє обов'язкову наявність числа, більшого будь-якого названого на 1. За цих умов правий край ряду натуральних чисел прийнято позначати символом нескінченності (значок ∞). Крім того, всяке натуральне число відноситься або до класу простих чисел, або до класу складених чисел; відповідно, ряд натуральних чисел складається з простих і складених чисел. Просте число ділиться без залишку тільки на себе і на 1, тому має лише два позитивних дільники. Натуральне число, яке ділиться без залишку ще на якесь натуральне число, крім самого себе і 1 називається складеним. Додатково по натуральних числах можна сказати наступне. Одиниця умовно вважається простим числом, хоча вона не є ні простим, ні складеним числом, адже одиниця має лише один позитивний дільник. Виходить так, що одиниця відповідає критерію простих чисел, бо ділиться на саму себе і на 1, хоча дільник насправді виходить один і той же. Двійка - той поодинокий випадок, коли в клас простих чисел потрапило парне число. Взагалі ж серед простих чисел більше немає жодного парного числа, оскільки інші парні числа більше 2 діляться як мінімум на 2. Простих чисел у ряді натуральних чисел теж нескінченна множина в тому сенсі, що прості числа продовжують з'являтися на всьому проміжку ряду натуральних чисел, а не перериваються в якійсь точці ряду. Прості числа (ті натуральні числа, які мають тільки два натуральних дільники: одиницю й саме себе) зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики. Два, три, п’ять, сім, одинадцять, тринадцять, сімнадцять... — щороку математики знаходять усе більші й більші прості числа. Якщо за часів Ейлера таким було 2147483647, то сьогоднішній рекордсмен — 2 у ступені 43112609 мінус 1 — у десятковому записі має 12978189 розрядів! Але математиків набагато більше за конкретні прості числа цікавлять пов’язані з ними закономірності: скільки їх, яка логіка їхньої появи серед натуральних чисел тощо. І якщо нескінченність кількості простих чисел зумів довести ще Евклід, то друге питання математики не можуть розв’язати досі. Світло на нього кинуло випадкове відкриття польсько-американського математика Станіслава Улама (до речі, наш співвітчизник — він народився в польському тоді Львові). Якось 1963 року, сидячи на нудній доповіді, учений почав за спіраллю заповнювати числами клітинки листка у зошиті, при цьому машинально відзначав серед них прості. Виявилося, що прості числа розташовуються не хаотично, а утворюють орнаменти з діагональних ліній. Сучасні комп’ютери будують такі «вишиванки» (математики не дуже шанобливо називають їх «скатертинами Улама») для десятків мільйонів чисел, і знайдена закономірність підтверджується. Однак підвести під цю «красу» міцний теоретичний фундамент поки не вдалося. Прості числа зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики. Просте число — це натуральне число, яке має рівно два натуральних дільники (лише 1 і саме число). Решту чисел, окрім одиниці, називають складеними. Таким чином, всі натуральні числа понад одиницю розбивають на прості і складені. Теорія чисел вивчає властивості простих чисел. В теорії кілець простим числам відповідають незвідні елементи. Натуральних чисел нескінченно багато. Найбільше натуральне число назвати в принципі неможливо, оскільки нескінченність ряду таких чисел розуміє обов'язкову наявність числа, більшого будь-якого названого на 1. За цих умов правий край ряду натуральних чисел прийнято позначати символом нескінченності (значок ∞). Крім того, всяке натуральне число відноситься або до класу простих чисел, або до класу складених чисел; відповідно, ряд натуральних чисел складається з простих і складених чисел. Просте число ділиться без залишку тільки на себе і на 1, тому має лише два позитивних дільники. Натуральне число, яке ділиться без залишку ще на якесь натуральне число, крім самого себе і 1 називається складеним. Одиниця умовно вважається простим числом, хоча вона не є ні простим, ні складеним числом, адже одиниця має лише один позитивний дільник. Виходить так, що одиниця відповідає критерію простих чисел, бо ділиться на саму себе і на 1, хоча дільник насправді виходить один і той же. Двійка - той поодинокий випадок, коли в клас простих чисел потрапило парне число. Взагалі ж серед простих чисел більше немає жодного парного числа, оскільки інші парні числа більше 2 діляться як мінімум на 2. Простих чисел у ряді натуральних чисел теж нескінченна множина в тому сенсі, що прості числа продовжують з'являтися на всьому проміжку ряду натуральних чисел, а не перериваються в якійсь точці ряду. Прості числа (ті натуральні числа, які мають тільки два натуральних дільники: одиницю й саме себе) зовсім не такі прості, як може здатися на перший погляд. Скоріше навпаки: серед різних чисел вони приховують, напевно, найбільшу кількість загадок, над якими от уже багато сторіч б’ються кращі математики. Два, три, п’ять, сім, одинадцять, тринадцять, сімнадцять... — щороку математики знаходять усе більші й більші прості числа. Якщо за часів Ейлера таким було 2147483647, то сьогоднішній рекордсмен — 2 у ступені 43112609 мінус 1 — у десятковому записі має 12978189 розрядів! Але математиків набагато більше за конкретні прості числа цікавлять пов’язані з ними закономірності: скільки їх, яка логіка їхньої появи серед натуральних чисел тощо. І якщо нескінченність кількості простих чисел зумів довести ще Евклід, то друге питання математики не можуть розв’язати досі.
1. Прості числа Керола
Прості числа вигляду (2n − 1)2 − 2. 7, 47, 223, 3967, 16127, 1046527, 16769023, 1073676287, 68718952447, 274876858367, 4398042316799, 1125899839733759, 18014398241046527, 1298074214633706835075030044377087 2. Центральні десятигранні прості числа Числа вигляду 5(n2 − n) + 1. 11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281, 6301, 6661, 7411, 9461, 9901, 12251, 13781, 14851, 15401, 18301, 18911, 19531, 20161, 22111, 24151, 24851, 25561, 27011, 27751 3. Центральні семигранні прості числа Числа вигляду (7n2 − 7n + 2) / 2. 43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697, 4663, 5741, 8233, 9283, 10781, 11173, 12391, 14561, 18397, 20483, 29303, 29947, 34651, 37493, 41203, 46691, 50821, 54251, 56897, 57793, 65213, 68111, 72073, 76147, 84631, 89041, 93563 4. Центральні квадратні прості числа Числа вигляду n2 + (n + 1)2. 5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613, 4513, 5101, 7321, 8581, 9661, 9941, 10513, 12641, 13613, 14281, 14621, 15313, 16381, 19013, 19801, 20201, 21013, 21841, 23981, 24421, 26681 5. Центральні трикутні прості числа Числа вигляду (3n2 + 3n + 2) / 2. 19, 31, 109, 199, 409, 571, 631, 829, 1489, 1999, 2341, 2971, 3529, 4621, 4789, 7039, 7669, 8779, 9721, 10459, 10711, 13681, 14851, 16069, 16381, 17659, 20011, 20359, 23251, 25939, 27541, 29191, 29611, 31321, 34429, 36739, 40099, 40591, 42589 6. Прості числа Мерсенна Прості числа вигляду 2n - 1. Перші 12 чисел: 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, 2305843009213693951, 618970019642690137449562111, 162259276829213363391578010288127, 170141183460469231731687303715884105727 На сьогоднішній день відомо 46 простих чисел Мерсенна. 7. Прості числа Маркова Прості числа p для яких існують цілі uта v такі, що u2 + v2 + p2 = 3uvp. 2, 5, 13, 29, 89, 233, 433, 1597, 2897, 5741, 7561, 28657, 33461, 43261, 96557, 426389, 514229 8. Прості числа Ферма Прості числа вигляду Відомі числа Ферма: 3, 5, 17, 257, 65537. 9. Прості числа Софі Жермен Прості числа p такі, що 2p + 1 також прості. 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, 173, 179, 191, 233, 239, 251, 281, 293, 359, 419, 431, 443, 491, 509, 593, 641, 653, 659, 683, 719, 743, 761, 809, 911, 953 10. Прості числа-близнюки (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883) 11. Прості числа з різницею 6 Пара простих чисел вигляду p, p + 6. Приклади пар простих чисел (5,11), (7,13), (11,17), (13,19), (17,23), (23,29), (31,37), (37,43), (41,47), (47,53), (53,59), (61,67), (67,73), (73,79), (83,89), (97,103), (101,107), (103,109), (107,113), (131,137), (151,157), (157,163), (167,173), (173,179), (191,197), (193,199), (223,229), (227,233), (233,239), (251,257), (257,263), (263,269), (271,277), (277,283), (307,313), (311,317), (331,337), (347,353), (353,359), (367,373), (373,379), (383,389), (433,439), (443,449), (457,463), (461,467). 12. Досконалічисла Досконале число — натуральне число, яке дорівнюєсумівсіхсвоїх дільників крім самого числа. Всьогоїхзнайдено 24. Числа, якіможнапредставити у вигляді 13. Дружні числа
Дружніми числами називають дванатуральні числатакі, що сума всіхдільниківпершого (за винятком самого числа) рівна другому числу, а сума всіхдільників другого числа (за винятком самого числа) рівнапершому числу. Наприклад для 220 такими дільниками є числа 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 і 110 сума якихрівна 284, а для 284 дільниками є 1, 2, 4, 71, і 142 сума якихрівна 220. Отже (220,284) є парою дружніх чисел. Найменшими парами дружніх чисел є (220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084). Завдання. Вибратитакі два (як мінімум) описані в методичцірізні типи простих чисел і знайти ті підмножиничислової спіралі, починаючи з заданого числа (центра спіралі), якій належать ці числа. Записати аналітичні вирази цих підмножин. Задане число має вигляд : k = 10 + L,де L – номер студента в загальному списку потоку (КН101 + КН102 + КН103 ). Побудувати можливе графічне представлення отриманих результатів (відзначити на своїй множині числа обраних типів).
Числові спіралі вибрати розмірністю не менше 17х17. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 151. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
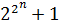 .
. , де
, де  - просте число (для того щоб число було простим необхідно, але недостатньо, щоб було простимчисло p). Усівідомідосідосконалі числа парні, проте не існує доведення того, щонепарнихдосконалих чисел немає.
- просте число (для того щоб число було простим необхідно, але недостатньо, щоб було простимчисло p). Усівідомідосідосконалі числа парні, проте не існує доведення того, щонепарнихдосконалих чисел немає.