
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Расчет по Алгоритму Краскала
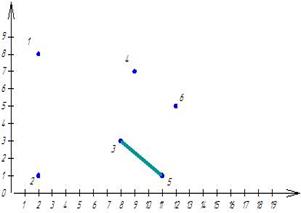
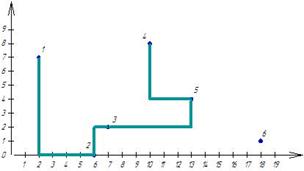
На плоскости в декартовой системе координат задано местоположение шести точек (рис. 5.1.). Расстояние  между любыми двумя точками между любыми двумя точками  и и 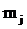 определено по формуле (5.1). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин определено по формуле (5.1). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин  не должны превышать двух – не должны превышать двух –  . .

Рисунок 5.1
Решение
Составляем матрицу длин и всем элементам, лежащим на главной диагонали и ниже нее, присваиваем значение  : :
| D=
|
| 1
| 2
| 3
| 4
| 5
| 6
| | 1
| ∞
| 7
| 7,8
| 7,1
| 6,3
| 11,4
| | 2
|
| ∞
| 6,3
| 9,2
| 9
| 10,8
| | 3
|
|
| ∞
| 4,1
| 3,6
| 4,5
| | 4
| ∞
|
| ∞
| 6,3
| 3,6
| | 5
|
|
|
|
| ∞
| 4,1
| | 6
|
|
|
|
|
| ∞
| Формируем таблицу меток и локальных степеней (см. табл. 5.1).
На нулевом шаге все вершины получают метки, равные их номерам  , а локальные степени , а локальные степени  , , 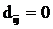 , длина строящегося дерева , длина строящегося дерева  и множество ребер в дереве êR ê= Æ. и множество ребер в дереве êR ê= Æ.
На первом шаге просматриваем элементы верхней половины матрицы D и выбираем из них минимальный элемент  (при наличии нескольких элементов с одинаковыми минимальными значениями выбираем элемент с наименьшими индексами i и j). (при наличии нескольких элементов с одинаковыми минимальными значениями выбираем элемент с наименьшими индексами i и j).
Таблица 5.1.
| Номер вершины
| Значения меток 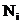 и степеней и степеней  вершин на очередном шаге вершин на очередном шаге
| | 0
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 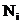
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 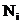
| 
| 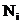
| 
| 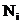
| 
| 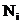
| 
| 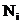
| 
| | 1
| 1
| 0
| 1
| 0
| 1
| 0
| 1
| 1
|
|
|
| 3
| 1
| 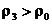
|  
| 3
| 2
| | 2
| 2
| 0
| 2
| 0
| 2
| 0
| 2
| 1
|
| 2
| 0
| 3
| 1
| | 3
| 3
| 0
| 3
| 1
| 3
| 1
| 3
| 2
| 3
| 2
| 3
| 2
| | 4
| 4
| 0
| 4
| 0
| 4
| 1
| 3
| 2
| 
|
| 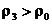
| 3
| 2
| 3
| 2
| | 5
| 5
| 0
| 3
| 1
| 3
| 1
| 3
| 1
|
|
| 3
| 2
| 3
| 2
| | 6
| 6
| 0
| 6
| 0
| 4
| 1
| 3
| 1
|
|
| 3
| 1
| 3
| 1
| 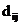
| 0
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 0
| 3,6
| 7,2
| 11,3
| 11,3
| 11,3
| 17,6
| 17,6
| 17,6
| 18,3
| 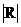
| 0
| 1
| 2
| 3
| 3
| 3
| 4
| 4
| 4
| 5
| | | | | | | | | | | | | | | | | | | | | | | | | |
Помечаем элемент 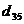 и на его место записываем и на его место записываем  . Метки у 3-й и 5-й вершин разные ( . Метки у 3-й и 5-й вершин разные (  , ,  ), поэтому соединяем вершины 3-ю и 5-ю ребром (см. Рис 5.2, а): метки у них становятся равными: ), поэтому соединяем вершины 3-ю и 5-ю ребром (см. Рис 5.2, а): метки у них становятся равными:  . Локальные степени обеих вершин равны единицам – . Локальные степени обеих вершин равны единицам –  и и  . .
Рис. 5.2.
Длина L строящегося дерева равна 3,6, а множество ребер êR ê = 1 (см. 1-й шаг табл. 1). На втором шаге выбирается минимальный элемент 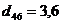 , на третьем – , на третьем –  (см. рис. 5.2, б,в). На места выбранных элементов в матрице D записываем (см. рис. 5.2, б,в). На места выбранных элементов в матрице D записываем 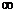 . Получили матрицу D1: . Получили матрицу D1:
| D=
|
| 1
| 2
| 3
| 4
| 5
| 6
| | 1
| ∞
| 7
| 7,8
| 7,1
| 6,3
| 11,4
| | 2
|
| ∞
| 6,3
| 9,2
| 9
| 10,8
| | 3
|
|
| ∞
| ∞
| ∞
| 4,5
| | 4
| ∞
|
| ∞
| 6,3
| ∞
| | 5
|
|
|
|
| ∞
| 4,1
| | 6
|
|
|
|
|
| ∞
|
В выделяемом минимальном дереве построены один фрагмент с суммарной длиной  . У вершин фрагмента (3-й, 4-й, 5-й, 6-й) метки . У вершин фрагмента (3-й, 4-й, 5-й, 6-й) метки  , а локальные степени - , а локальные степени -  , ,  . .
Выбранный из оставшихся минимальный элемент  , на очередном 4-м шаге, не может быть включен во множество R ребер дерева, поскольку образует цикл с ребрами ранее построенного фрагмента (на это указывают одинаковые метки у 5-й и 6-й вершин , на очередном 4-м шаге, не может быть включен во множество R ребер дерева, поскольку образует цикл с ребрами ранее построенного фрагмента (на это указывают одинаковые метки у 5-й и 6-й вершин  ).(см. рис. 5.2, г). ).(см. рис. 5.2, г).
На пятом шаге выбранные ребра 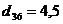 соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, д). соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, д).
Выбранный из оставшихся минимальный элемент  , на очередном 6-м шаге, метки у 1-й и 5-й вершин разные ( , на очередном 6-м шаге, метки у 1-й и 5-й вершин разные (  , ,  ), поэтому соединяем вершины 1-ю и 5-ю ребром (см. Рис 5.2, е): метки у них становятся равными: ), поэтому соединяем вершины 1-ю и 5-ю ребром (см. Рис 5.2, е): метки у них становятся равными:  . Локальные степени обеих вершин равны единицам – . Локальные степени обеих вершин равны единицам –  и и  . .
На седьмом шаге выбранные ребра  соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, ж) соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, ж)
На восьмом шаге выбранные ребра  соответственно образует цикл, и их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, з) соответственно образует цикл, и их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, з)
На девятом шаге присоединяется ребро  , при этом выполняется условие , при этом выполняется условие  , т. е. дерево построено: , т. е. дерево построено:  , длина дерева , длина дерева  (рис. 5.3). (рис. 5.3).

Рис. 5.3
Машинный расчет по Алгоритму Краскаля

Рис. 5.5 (а)

Рис. 5.5 (б)

\ Рис. 5.5 (в)

Рис. 5.5 (г)

Рис. 5.5 (д)

Рис. 5.5 (е)
В результате машинного расчета решения дерево построено:  , длина дерева , длина дерева  (см. рис. 5.5, а-е). (см. рис. 5.5, а-е).
Расчет по Алгоритму Прима
На плоскости в декартовой системе координат задано местоположение шести точек (рис. 5.5). Расстояние между любыми двумя точками  и и 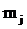 определено по формуле (5.2). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин определено по формуле (5.2). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин  не должны превышать двух: не должны превышать двух:  . .
Решение
Составляем матрицу расстояний
Просматриваем все строки матрицы и выбираем элемент, являющийся минимальным. Поскольку таких элементов два 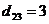 . Помечаем его, локальные степени 2-й и 3-й вершин увеличиваем на единицу – . Помечаем его, локальные степени 2-й и 3-й вершин увеличиваем на единицу –  . Исключаем из рассмотрения (вычеркиваем) все элементы второго и третьего столбцов. Соединяем . Исключаем из рассмотрения (вычеркиваем) все элементы второго и третьего столбцов. Соединяем  и и  (рис. 5.6, а). (рис. 5.6, а).
Просматриваем вторую и третью строки матрицы. Выбираем элемент  ; локальные степени 3-й и 5-й вершин увеличиваем на единицу – ; локальные степени 3-й и 5-й вершин увеличиваем на единицу –  ; ;  . Исключаем из рассмотрения элементы 5-го столбца и 3-й строки (к 3-й вершине . Исключаем из рассмотрения элементы 5-го столбца и 3-й строки (к 3-й вершине  подключено уже два ребра). Соединяем подключено уже два ребра). Соединяем  с с  (рис. 5.6, б). Получили матрицу D1: (рис. 5.6, б). Получили матрицу D1:
Просматриваем вторую и пятую строки. Выбираем элемент  ; ;  ; ;  . Соединяем вершины . Соединяем вершины  и и  (рис. 5.6, в). Исключаем из рассмотрения четвертый столбец и пятую строку, поскольку (рис. 5.6, в). Исключаем из рассмотрения четвертый столбец и пятую строку, поскольку  . .
Просматриваем вторую и четвертую строки. Выбираем элемент  ; ;  ; ;  . Соединяем . Соединяем  с с  (рис. 5.6, г). Поскольку (рис. 5.6, г). Поскольку  , исключаем из рассмотрения первый столбец и вторую строку. И, наконец, просматриваем первую и четвертую строки. Выбираем , исключаем из рассмотрения первый столбец и вторую строку. И, наконец, просматриваем первую и четвертую строки. Выбираем 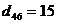 ; ;  , ,  . Соединяем . Соединяем  с с  (рис. 5.6, д). Исключаем из рассмотрения последний шестой столбец. (рис. 5.6, д). Исключаем из рассмотрения последний шестой столбец.
Минимальное связывающее дерево, полученное в результате решения, приведено на рис.5.6, д.
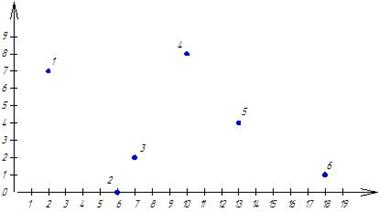
Рис. 5.5
Рис. 5.6
Множество ребер в нем 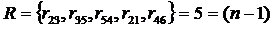 . Суммарная длина его ребер L равна 43. . Суммарная длина его ребер L равна 43.
|

 между любыми двумя точками
между любыми двумя точками  и
и 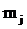 определено по формуле (5.1). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин
определено по формуле (5.1). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин  не должны превышать двух –
не должны превышать двух –  .
.
 :
: , а локальные степени
, а локальные степени  ,
, 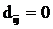 , длина строящегося дерева
, длина строящегося дерева  и множество ребер в дереве êR ê= Æ.
и множество ребер в дереве êR ê= Æ. (при наличии нескольких элементов с одинаковыми минимальными значениями выбираем элемент с наименьшими индексами i и j).
(при наличии нескольких элементов с одинаковыми минимальными значениями выбираем элемент с наименьшими индексами i и j).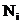 и степеней
и степеней  вершин на очередном шаге
вершин на очередном шаге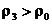



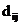










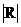
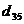 и на его место записываем
и на его место записываем  . Метки у 3-й и 5-й вершин разные (
. Метки у 3-й и 5-й вершин разные (  ,
,  ), поэтому соединяем вершины 3-ю и 5-ю ребром (см. Рис 5.2, а): метки у них становятся равными:
), поэтому соединяем вершины 3-ю и 5-ю ребром (см. Рис 5.2, а): метки у них становятся равными:  . Локальные степени обеих вершин равны единицам –
. Локальные степени обеих вершин равны единицам –  и
и  .
. а)
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
 е)
е)
 ж)
ж)
 з)
з)
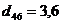 , на третьем –
, на третьем –  (см. рис. 5.2, б,в). На места выбранных элементов в матрице D записываем
(см. рис. 5.2, б,в). На места выбранных элементов в матрице D записываем  . У вершин фрагмента (3-й, 4-й, 5-й, 6-й) метки
. У вершин фрагмента (3-й, 4-й, 5-й, 6-й) метки  , а локальные степени -
, а локальные степени -  ,
,  .
. , на очередном 4-м шаге, не может быть включен во множество R ребер дерева, поскольку образует цикл с ребрами ранее построенного фрагмента (на это указывают одинаковые метки у 5-й и 6-й вершин
, на очередном 4-м шаге, не может быть включен во множество R ребер дерева, поскольку образует цикл с ребрами ранее построенного фрагмента (на это указывают одинаковые метки у 5-й и 6-й вершин  ).(см. рис. 5.2, г).
).(см. рис. 5.2, г).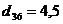 соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, д).
соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, д). , на очередном 6-м шаге, метки у 1-й и 5-й вершин разные (
, на очередном 6-м шаге, метки у 1-й и 5-й вершин разные (  ,
,  ), поэтому соединяем вершины 1-ю и 5-ю ребром (см. Рис 5.2, е): метки у них становятся равными:
), поэтому соединяем вершины 1-ю и 5-ю ребром (см. Рис 5.2, е): метки у них становятся равными:  . Локальные степени обеих вершин равны единицам –
. Локальные степени обеих вершин равны единицам –  и
и  .
. соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, ж)
соответственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, ж) соответственно образует цикл, и их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, з)
соответственно образует цикл, и их присоединение нарушает ограничение на локальную степень 3-й вершины. (см. рис. 5.2, з) , т. е. дерево построено:
, т. е. дерево построено:  , длина дерева
, длина дерева  (рис. 5.3).
(рис. 5.3).






 , длина дерева
, длина дерева  (см. рис. 5.5, а-е).
(см. рис. 5.5, а-е).
 1
1

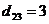 . Помечаем его, локальные степени 2-й и 3-й вершин увеличиваем на единицу –
. Помечаем его, локальные степени 2-й и 3-й вершин увеличиваем на единицу –  . Исключаем из рассмотрения (вычеркиваем) все элементы второго и третьего столбцов. Соединяем
. Исключаем из рассмотрения (вычеркиваем) все элементы второго и третьего столбцов. Соединяем  и
и  (рис. 5.6, а).
(рис. 5.6, а). ; локальные степени 3-й и 5-й вершин увеличиваем на единицу –
; локальные степени 3-й и 5-й вершин увеличиваем на единицу –  ;
;  . Исключаем из рассмотрения элементы 5-го столбца и 3-й строки (к 3-й вершине
. Исключаем из рассмотрения элементы 5-го столбца и 3-й строки (к 3-й вершине  (рис. 5.6, б). Получили матрицу D1:
(рис. 5.6, б). Получили матрицу D1: ;
;  ;
;  (рис. 5.6, в). Исключаем из рассмотрения четвертый столбец и пятую строку, поскольку
(рис. 5.6, в). Исключаем из рассмотрения четвертый столбец и пятую строку, поскольку  .
. ;
;  ;
;  (рис. 5.6, г). Поскольку
(рис. 5.6, г). Поскольку  , исключаем из рассмотрения первый столбец и вторую строку. И, наконец, просматриваем первую и четвертую строки. Выбираем
, исключаем из рассмотрения первый столбец и вторую строку. И, наконец, просматриваем первую и четвертую строки. Выбираем 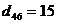 ;
;  ,
,  . Соединяем
. Соединяем  (рис. 5.6, д). Исключаем из рассмотрения последний шестой столбец.
(рис. 5.6, д). Исключаем из рассмотрения последний шестой столбец.
 а)
а)
 б)
б)
 в)
в)
 г)
г)

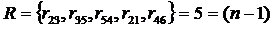 . Суммарная длина его ребер L равна 43.
. Суммарная длина его ребер L равна 43.