Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общие сведения из задачи компоновкиУЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Заочно-вечерний факультет Кафедра «Проектирования и Технология Электронных Средств»
Лабораторная работа № 2 ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМА КОМПОНОВКИ СХЕМ РАДИОЭЛЕКТРОННЫХ СРЕДСТВ
Работу выполнил: Работу принял: студент группы Рбв-31 преподаватель кафедры Латыпов М.Р. Мактас М.Я. _____________ _______________
Ульяновск 2018 Цель работы.
Исследовать эффективность последовательного метода компоновки конструктивных элементов и узлов РЭС в узлы высшего уровня; усвоить особенности алгоритмизации и программирования задачи компоновки конструктивных элементов на ПЭВМ; приобрести навыки построения математических моделей объектов конструирования, реализации и исследования их при решении задачи компоновки в САПР.
Общие сведения из задачи компоновки В настоящее время в радиоэлектронике принят функционально-узловой метод проектирования [1 – 7]. Он предусматривает расчленение радиоэлек-тронных средств (РЭС) на отдельные конструктивно законченные единицы (модули) различных уровней (рангов). Это могут быть отдельные платы – ти-повые элементы замены (ТЭЗы), функциональные узлы, субблоки, блоки, па-нели, пульты, стойки. В связи с этим при разработке конструкций РЭС проек-тировщик неизбежно сталкивается с задачей распределения элементов схемы низшего уровня по коммутационным пространствам модулей данного уровня иерархии. При ее решении основным критерием оптимальности компоновки модулей является минимизация числа межмодульных связей, что необходимо для повышения надежности схем (за счет уменьшения числа разъемных соеди-нений), уменьшения влияния наводок и времени задержки сигнала в цепях (вследствие минимизации суммарной длины соединений), упрощения кон-струкции и повышения технологичности разрабатываемого устройства. 
2.1. Математическая формулировка задачи Для алгоритмизации и формального решения задачи компоновки РЭС производится переход от электрической схемы соединений РЭС к мультиграфу. При этом каждому конструктивному элементу (модулю) ставят в соответствии вершину мультиграфа, а электрическим связям схемы – его ребра. В этом случае задача компоновки формулируется следующим образом [2 – 5]. Дан мультиграф
При разбиении графа на куски
где Uij – множество ребер, соединяющих куски Другими словами, совокупность кусков разбиения графа
и для любых двух кусков В выражении (2.4) множество Конструктивными ограничениями в задачах компоновки являются: а) максимально допустимое количество вершин t в куске
б) число кусков разрезания графа
где l – количество вершин в исходном графе; в) максимальное число внешних связей каждого отдельного куска
Физический смысл ограничений (2.2) – (2.9) следующий. Условия (2.2) – (2.4) означают, что не может быть двух узлов, содержащих один и тот же элемент, вместе с тем электрические цепи, соединяющие отдельные узлы существуют. Условие (2.5) – суммарное число элементов, входящих в отдельные узлы, равно количеству элементов, входящих в электрическую схему всего устройства. Условие (2.6) – не может быть узла, в котором не содержится ни одного элемента. Условие (2.7) – соответствует числу конструктивных элементов, которые необходимо разместить в коммутационном пространстве, (2.8) – требуемое число узлов, в которые требуется скомпоновать конструктивные элементы устройства, (2.9) – определяет количество контактов используемого разъема. Для оценки качества компоновки схемы в узлы, что соответствует оценке качества разбиения на куски, введем понятие коэффициента разбиения
Каждое подмножество
……………………………
где Тогда отношение суммарного числа внутренних ребер (ребер подмножеств
Коэффициент разбиения Существует значительное количество алгоритмов компоновки, которые мо-жно условно разбить на пять групп: 1) последовательные алгоритмы; 2) итера-ционные алгоритмы; 3) алгоритмы, использующие методы целочисленного программирования; 4) алгоритмы, основанные на решении задачи о назначе-нии; 5) смешанные алгоритмы.
2.2. Последовательные алгоритмы компоновки Суть последовательных алгоритмов заключается в том, что вначале по определенному признаку выбирают вершину или группу вершин, к которым затем присоединяют другие вершины графа для образования первого куска. Процесс повторяют до получения заданного разбиения.
2.3. Метод максимальной конъюнкции – минимальной дизъюнкции Основной критерий разбиения графа на куски – минимум числа соединяющих ребер между кусками графа. Если формировать куски Рассмотрим метод максимальной конъюнкции – минимальной дизъюнкции [1, 4]. Пусть дана схема с множеством элементов Работа начинается с формирования 1-го узла. Первым выбирается элемент, подключенный к наибольшему числу цепей. Далее последовательно оцениваются по двум параметрам возможности назначения в формируемый узел оставшихся элементов. Вначале отбирается множество элементов, назначение каждого из которых в формируемый узел не превышает предельно допустимого числа z внешних связей узла. Затем из полученного множества элементов выбираются такие, которые имеют с назначенными в формируемый узел элементами наибольшее число общих цепей. При работе алгоритма схема представляется в виде графа Кенига
2.4 Алгоритм
1. Ввод матрицы 2. По матрице
3. Из множества нераспределенных вершин E выбираем вершину 4. Назначаем выбранную вершину 5. Строку
6. Определяем суммы элементов 7. Из множества строк 8. Если 9. Строку
10. Определяем суммы 11. Из множества строк 12. Вершину 13. Если 14. Определяем множество нераспределенных элементов 15. Составляем матрицу 16. Идти к 5. 17. Узел 18. Идти к 2. 19. Конец.
Экспериментальная часть
Рисунок 1.
На Рис.1 представлена схема электрическая принципиальная.
По матрице
Максимальную локальную степень, равную 4, имеет вершина
Находим суммы элементов в дизъюнкциях: Выбираем вершины, имеющие Выполним конъюнкцию 7-й строки со строкой отобранных элементов
Величина Поскольку по условию в узел необходимо включить четыре элемента, то переходим к подбору следующей вершины. Для этого модифицируем матрицу Вместо 7-й и 2-й строк в ней запишем дизъюнкцию этих строк. Получим матрицу Q2:
Снова вычисляем дизъюнкции строки
Результаты суммирований запишем справа от каждой строки матрицы
Справа от матрицы Поскольку по условию в узел необходимо включить четыре элемента, то переходим к подбору следующей вершины.
Для этого модифицируем матрицу Вместо 2-й, 10-й и 8-й строк в ней запишем дизъюнкцию этих строк. Получим матрицу Q3:
Снова вычисляем дизъюнкции строки
Результаты суммирований запишем справа от каждой строки матрицы
Справа от матрицы Итак, узел Аналогично формируем второй узел
После определения локальных степеней вершин первой в формируемый узел Вычисление дизъюнкции и конъюнкции строки
|
 . Требуется разбить («разрезать») его на отдельные куски
. Требуется разбить («разрезать») его на отдельные куски  ,
, 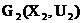 ,…,
,…,  так, чтобы число ребер, соединяющих эти куски, было минимальным. Это значит надо минимизировать функцию:
так, чтобы число ребер, соединяющих эти куски, было минимальным. Это значит надо минимизировать функцию: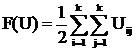 , где
, где  (2.1)
(2.1) ,
,  задаются следующие ограничения:
задаются следующие ограничения: , (2.2)
, (2.2) , (2.3)
, (2.3) , (2.4)
, (2.4) ;
;  , (2.5)
, (2.5) и
и  .
. является разбиением графа G, если любой кусок из этой совокупности не пустой
является разбиением графа G, если любой кусок из этой совокупности не пустой , (2.6)
, (2.6) пересечение множества вершин – пустое множе-ство (2.3), а пересечение множества ребер (2.4) может быть не пустым. Кроме этого объединение всех кусков (2.5) должно в точности равняться графу G.
пересечение множества вершин – пустое множе-ство (2.3), а пересечение множества ребер (2.4) может быть не пустым. Кроме этого объединение всех кусков (2.5) должно в точности равняться графу G. определяет подмножество ребер
определяет подмножество ребер  , попадающих в разрез (сечение) между кусками
, попадающих в разрез (сечение) между кусками 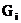 и
и  графа G.
графа G. ; (2.7)
; (2.7) , (2.8)
, (2.8) . (2.9)
. (2.9) . Для этого допустим, что граф G разбит на k кусков:
. Для этого допустим, что граф G разбит на k кусков:  . Тогда множество ребер U графа G можно представить в виде
. Тогда множество ребер U графа G можно представить в виде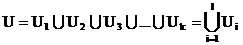 . (2.10)
. (2.10) запишем следующим образом:
запишем следующим образом: ,
, (2.11)
(2.11) ,
, куска
куска 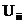 – подмножество ребер, соединяющих подмножество вершин
– подмножество ребер, соединяющих подмножество вершин  ) – подмножество ребер, соединяющих куски
) – подмножество ребер, соединяющих куски  . (2.12)
. (2.12)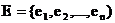 , соединенных между собой множеством электрических цепей
, соединенных между собой множеством электрических цепей  . Ее необходимо скомпоновать в узлы, включающие по t элементов. Число внешних связей узлов не должно превышать z (z – число контактов в разъеме).
. Ее необходимо скомпоновать в узлы, включающие по t элементов. Число внешних связей узлов не должно превышать z (z – число контактов в разъеме). , в котором подмножество вершин E и V интерпретируют соответственно множества элементов E и электрических цепей V. При этом вершина
, в котором подмножество вершин E и V интерпретируют соответственно множества элементов E и электрических цепей V. При этом вершина 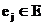 соединяется с вершиной
соединяется с вершиной  ребром
ребром  в том случае, когда элемент
в том случае, когда элемент  принадлежит цепи
принадлежит цепи 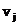 . Для вычисления на ЭВМ граф
. Для вычисления на ЭВМ граф  , в которой число строк n определяется количеством элементов схемы, а столбцов m – количеством электрических цепей. Элемент
, в которой число строк n определяется количеством элементов схемы, а столбцов m – количеством электрических цепей. Элемент  , стоящий на пересечении i-й строки и j-го столбца, равен 1, если элемент
, стоящий на пересечении i-й строки и j-го столбца, равен 1, если элемент  .
. :
: .
. .
. , формируемого узла.
, формируемого узла. матрицы
матрицы 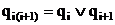 ;
;  ;…
;… в модифицированных строках
в модифицированных строках  .
. выбираем такие, в которых
выбираем такие, в которых  . Объединяем их во множество
. Объединяем их во множество  .
. , то переходим к 17, иначе к 9.
, то переходим к 17, иначе к 9. матрицы
матрицы  ;…
;… элементов в модифицированных строках
элементов в модифицированных строках  .
. .
. , дающую
, дающую  назначаем в формируемый узел
назначаем в формируемый узел  .
. , то идти к 17, иначе к 14.
, то идти к 17, иначе к 14.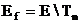 . Если
. Если  , то идти к 19, иначе к 15.
, то идти к 19, иначе к 15. . Для чего в исходной матрице
. Для чего в исходной матрице  , записываем дизъюнкцию всех указанных строк.
, записываем дизъюнкцию всех указанных строк. .
.
 исходного графа определяем локальные степени вершин и приписываем их справа к каждой строке матрицы (число цепей, подключенных к каждому элементу схемы):
исходного графа определяем локальные степени вершин и приписываем их справа к каждой строке матрицы (число цепей, подключенных к каждому элементу схемы):
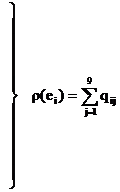
 . Выполним дизъюнкции 1-й строки
. Выполним дизъюнкции 1-й строки 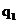 , соответствующей
, соответствующей  , с остальными строками:
, с остальными строками:
 ,
,
 и т. д.
и т. д. ,
,  , ,
, ,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. , и включение которых в формируемый узел не превысит условия
, и включение которых в формируемый узел не превысит условия  . Такой является вершина
. Такой является вершина  , у которых
, у которых  .
. :
:
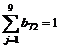 ,
,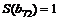 , и включаем ее в узел
, и включаем ее в узел  .
.



 со всеми остальными и определяем суммы элементов в них.
со всеми остальными и определяем суммы элементов в них.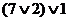
 ,
,
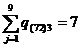 и т. д.
и т. д.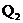 . Минимальную
. Минимальную  имеет
имеет  с остальными строками и суммирования элементов в результирующих строках получим
с остальными строками и суммирования элементов в результирующих строках получим
 ,
,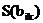 . Максимальное значение
. Максимальное значение  :
: 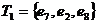 .
.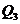 .
.

 со всеми остальными и определяем суммы элементов в них.
со всеми остальными и определяем суммы элементов в них.
 ,
,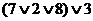
 и т. д.
и т. д. имеют
имеют 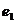 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  и
и  . После выполнения конъюнкции строки (
. После выполнения конъюнкции строки (  с остальными строками и суммирования элементов в результирующих строках получим:
с остальными строками и суммирования элементов в результирующих строках получим:
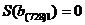

 ,
, имеет вершина
имеет вершина  .
. , рассматривая оставшиеся вершины
, рассматривая оставшиеся вершины 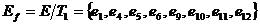 . Для этого из исходной матрицы
. Для этого из исходной матрицы  . Получим:
. Получим:




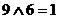





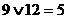
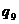 , соответствующей
, соответствующей  ) позволило назначить в узел
) позволило назначить в узел  :
: