Зависимость между дирекционными углами и румбами

Например: a= 241°00¢0, т.е. сторона направлена между 180° и 270°; следовательно, румб будет назван - ЮЗ; а градусная величина его будет

241° - 180° = 61°

Горизонтальные проложения сторон выписываются в ведомость из абриса или соответствующего журнала с учетом поправок за компарирование и температуру .

Например, выписывают значения:

D _I-II=102,50 м ;

D_II-III=109,65 м и т.д.

Под итоговой чертой вычисляется сумма всех горизонтальных проложений – периметр полигона.

Например: ΣD=846,12 м.

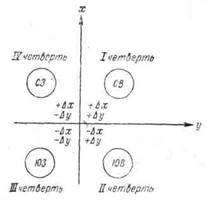
Рисунок 27

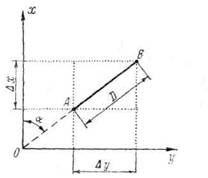
Вычисление приращений координат.

Знак приращения зависит от названия координатной четверти, в которой направлена данная сторона хода, и определяется по схеме (Рисунок 27.).

Например, для направления ЮЗ

Dх имеет знак минус (-)

Dу « « « (-)

Величины приращений находятся по “Таблицам приращений координат”, составленным на основе формул:

Dх = D cos a;

Dу = D sin a;

что видно из рисунка 28

Рисунок 28

Приращения рекомендуется вычислять, пользуясь “Пятизначными таблицами натуральных значений sin и cos”, и калькулятором. В этом случае выбранные из таблиц значение sin и cos надо лишь перемножить на длину стороны.

Вычисленные приращения округляются до сантиметров и вписываются в графу “Приращения вычисленные”.

Например:

DX = - 49, 69;

DY = - 89, 65.

Определение линейной невязки.

Для этого сначала составляют суммы всех вычисленных приращений DX положительных (SDX+) и отрицательных (SDX-), а затем их алгебраическую сумму, которая для случая замкнутого полигона и будет величиной невязки по оси абсцисс.

¦_х = S DX .

Аналогично действуют, вычисляя невязку по оси ординат

п

¦_y = S DY ;

¦_y = (+279,03) + (-273,50) = -0,27.

Абсолютная линейная невязка в периметре полигона определяется по формуле:

ƒ_D = √ (ƒ_х)² + (ƒ_y)²

Например:

¦_D = √ (0,03 )² + (0,27)² = ± 0, 28.

Относительная линейная невязка определяется отношением абсолютной невязки к периметру полигона.

¦_D / SD = 0,28 / 846,12 » 1 / 3000,

где SD - периметр полигона.

Если полученная относительная линейная невязка не превышает 1/2000, то результаты считаются благополучными, и можно распределять невязки, полученные по осям координат.

Если ¦_D / SD > 1 / 2000 , то необходимо тщательно проверить вычисления и при необходимости произвести повторные измерения.

Если ¦_D / SD < 1 / 2000 , то производится распределение невязки ¦х и ¦y путем введения поправок в вычисленные приращения DC и DY пропорционально длинам сторон:

(¦x / SD)´D_n и (¦y / SD)´D_n

где D_n - длина горизонтального проложения соответствующей стороны.

Поправка вводится со знаком, обратным знаку невязки. Так как при этом поправка может выражаться лишь долями сантиметра, то надо ее округлить до целого сантиметра и вводить только в приращения, соответствующие наибольшим сторонам.

Если ¦x = 0,03, то поправки по 1 см. вводятся только в приращения, соответствующие лишь большим сторонам III - IV, V - VI, VI - VII.

Во всех случаях сумма поправок должна равняться величине полученной невязки, но с обратным знаком.

Исправленные (увязанные) приращения вычисляются как алгебраическая сумма вычисленных приращений и соответствующих поправок.

Например:

(DY_I-II) _испр = (-89,65) + (+0,03) = - 89,62

Контроль увязки приращений: в замкнутом полигоне алгебраическая сумма исправленных приращений по каждой оси должна равняться нулю.

Вычисление координат вершин полигона.

Координаты точки I заданы

Х_I = 0,00; Y_I = 0,00.

Координаты последующих точек вычисляются по формулам:

Х_n = Х _n-1 + (DC) _испр; Y_n = Y _n-1+ (DY) _испр,

где

Например:

Х_III = (-49,69) + (+105,26) = +55,57;

Y_III = (-89,62) + (+ 30,71) = -58,91.

Если к координатам последней точки прибавить приращения по последней замыкающей стороне, то должны получиться координаты первой точки, что и будет контролем правильности вычисления координат вершин замкнутого теодолитного хода.

Например:

(+ 93,73) + (- 93,73) = 0,00;

(+ 55,80) + (- 55,80) = 0,00.

Ведомость вычисления координат вершин теодолитного хода