
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод Циклического покоординатного спуска
В данном методе на каждой итерации выполняется n(количество координат) одномерных минимизаций (спусков) вдоль единичных орт. Этот метод работает особенно хорошо, если линии равного уровня расположены вдоль координатный осей. Начальный этап Выбрать x1, e, k=1, l=1. Основной этап Шаг 1 (1) В качестве направления p выбрать (2) Найти L как результат минимизации функции по направлению p. (3) (4) Если l<n то Шаг 2, иначе повторить Шаг 1 с l = l+1. Шаг 2 (1) Вычислить (2) Проверить КОП: если
Метод параллельных касательных
Начальный этап: Выбрать х1, ε = 10-4 – 10-8 установить k = 1; Основной этап: Шаг 1. Из точки x1 выполнить антиградиентный в точку x2= x1+α1р1, где p1=-Ñу1. Шаг 2. Последовательно выполнить две операции: 1. Антиградиентный спуск в точку x3. 2. Вычислить ускоряющее направление d=x3-x1 и, не останавливаясь совершить ускоряющий шаг в точку x4=x3+α3d. Шаг 3. Проверить КОП: Иначе: 1. Обозначить x2 как новую начальную x1=x2, а точку x4 как новую точку ускорения x2=x4. Перейти к шагу 2. Метод Гаусса-Зейделя Начальный этап Выбрать х1, ε = 10-4 – 10-8 установить k = 1; Основной этап: Шаг 1. Выполнить серию одномерных поисков вдоль координатных орт
Шаг 2. Вычислить ускоряющее направление и проверить КОП: Иначе: 1. Выполнить ускоряющий шаг в новую точку хn+2 2. Обозначить последнюю точку как начальную и вернуться на шаг 1.
Метод комплексов Бокса
Комплекс-метод предназначен для отыскания условного экстремума непрерывной целевой функции (1) в выпуклой допустимой области.  При использовании метода принимаются следующие предположения: 1. Задача поиска экстремума функционала (1) решается при наличии ограничений 1-го и 2-го рода. 2. Значения целевой функции и функций ограничений могут быть вычислены в любой точке допустимой области изменения независимых переменных. 3. Допустимая область выпукла. 4. Значения целевой функции и функций ограничений вычисляются без ошибок. Идея комплекс метода заключается в последовательной замене точек некоторой конфигурации, удаленных от экстремума, на более близкие к нему. В отличие от симплексного метода, в комплексе-методе используется случайный набор N точек – Комплекс, а число точек Комплекса определяется по правилу:
 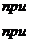 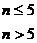
где n – число независимых переменных. Вычислительная последовательность (алгоритм) комплекс-метода включает в себя следующие этапы. 1) Формируется исходный комплекс. Координаты вершин исходного Комплекса хij вычисляются последовательно с помощью равномерно распределенных на интервале (0;1) псевдослучайных чисел rij:
В каждой вершине с номером j проверяется выполнение ограничений 2-го рода (ограничения 1-го рода выполняются автоматически). Точка фиксируется как вершина Комплекса, если в ней удовлетворяются все ограничения. Если же ни в одной из точек ограничения не выполнены, то формуле (6) вычисляются координаты новых точек, в которых вновь проверяется ограничения. Пусть число точек, удовлетворяющих ограничениям 2-го рода Р (Р≥1), тогда (N–P) – число точек, в которых ограничения нарушены. Далее для каждой из еще незафиксированных вершин выполняется операция по ее смещению к центру Р вершин Комплекса, при этом новые координаты точки х*ij вычисляются по формуле
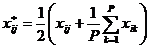 , i=1, 2,…, n, j=P+1, P+2,…,N. , i=1, 2,…, n, j=P+1, P+2,…,N.
Процесс смещения j-й точки продолжается до тех пор, пока для нее не будут выполнены все ограничения. Такой момент обязательно наступит, поскольку допустимая область выпукла. Точка фиксируется как новая вершина Комплекса (Р увеличивается на единицу), после чего операция смещения повторяется для очередной вершины.
Fj=F(xj),
R=FG; S=FD. где G – номер самой «хорошей»; а D – самой «плохой» вершины. 4) Определяются координаты Ci центра Комплекса с отброшенной «наихудшей» вершиной:
 , i=1, 2,…,n. , i=1, 2,…,n.
5) Проверяется условие окончания поиска. Для этого вычисляется величина В:
 . .
Если В<ε (ε – заданная точность вычисления), т.е. среднее расстояние от центра Комплекса до худшей (D) и лучшей (G) вершин меньше ε, то поиск заканчивают, считая экстремум найденным. В противном случае вычисления продолжаются:
xi0=2,3Ci – 1,3xiD, i=1, 2,…,n. В этой новой точке проверяется выполнение ограничений 1-го рода. В случае, если ограничения нарушаются, xi0 принимает значения gi+ε или hi–ε в зависимости от того, в какую сторону i-е ограничение нарушено;
Процесс смещения продолжают до тех пор, пока все ограничения 2-го рода не будут соблюдены. 8) В новой точке вычисляют значения целевой функции F0:
  . .
Затем вновь вычисляют значение целевой функции F0 и сравнивают его с S. Смещением к лучшей вершине по формуле (15) продолжают до тех пор, пока F0 не станет лучше S. За счет этой процедуры происходит последовательное сжатие комплекса к лучшей вершине. 10) Если вычисленное в новой точке х0 значение F0 лучше S, то в Комплексе на месте наихудшей точки хD фиксируется точка х0 и значение S заменяется на F0. Затем вычисления повторяются, начиная с п. 3, и продолжаются до тех пор пока не будет выполнено условие остановки, т.е. не будет найден с заданной точностью экстремум целевой функции. |
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 366. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
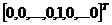 , где ненулевая позиция имеет индекс l.
, где ненулевая позиция имеет индекс l.

 , то
, то  , иначе
, иначе  , l=1 и на Шаг 1.
, l=1 и на Шаг 1. - остановиться x*=x4.
- остановиться x*=x4.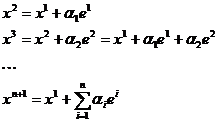
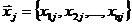 , j=1, 2,…,N.
, j=1, 2,…,N. .
. .
.