Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение эффективной скорости передачи данных и оптимальной длины блоков для системы РОС-ОЖ.Стр 1 из 2Следующая ⇒ РАСЧЕТ ПАРАМЕТРОВ СИСТЕМЫ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
Методические указания к курсовому проектированию
210400,210406
САНКТ-ПЕТЕРБУРГ 2011
Расчет параметров системы передачи дискретных сообщений.
Целью курсового проектирования является закрепление и расширение теоретических и практических знаний, полученных в процессе обучения, а также приобретение навыков решения инженерных задач. Задача, которую решают студенты при выполнении курсовой работы, состоит в расчете основных параметров системы передачи данных, к числу которых относятся: эффективная скорость передачи данных ( скорость передачи символов данных, определяемая отношением числа символов, принятых получателем данных к общему времени передачи), достоверность передачи данных. Также предложено рассмотреть методику построения образующей матрицы и матрицы проверок для заданного циклического кода, построения таблицы всех разрешенных кодовых комбинаций и определение доли необнаруженных ошибок. Следует рассмотреть эффективность передачи данных заданным кодом в канале передачи с независимыми ошибками и в канале с группированием ошибок. Особым вопросом, представляющим определенные трудности для рассмотрения, является изучение методов программной реализации циклических кодов и написание программ, иллюстрирующих процедуры кодирования и декодирования. В качестве исходных данных задаются такие параметры как : - модель дискретного канала; - способ модуляции; - используемый алгоритм решающей обратной связи; - помехоустойчивые коды для обнаружения и исправления ошибок, возникающих в процессе передачи данных. 
Варианты заданий и исходных данных к курсовой работе. Студенты группы разбиваются на 5 подгрупп, номер которой определяет метод программной реализации циклического кода. Студенты получают и порядковый номер от 1 до N, где N – количество студентов в группе, что определяет вид образующего полинома и характеристики дискретного канала В табл. 1 приводятся параметры циклического кода и вид образующего полинома в соответствии с порядковым номером студента в группе. В табл.2 приводятся значения вероятности ошибки в канале связи p0, коэффициента группирования α и емкости накопителя в системе РОС – НП h.
Таблица №1
Таблица №2
Таблица 3
Таблица 4
Каждой подгруппе студентов выдается один из пяти методов программной реализации циклических кодов: - матричный метод - матричный метод с использованием транспонированной матрицы проверок HT - метод с использованием проверочных соотношений - табличный метод -имитационное моделирование кодирующего и декодирующего устройства. Для расчета максимальной скорости передачи данных исходные данные приводятся в табл. 3 и 4.
2. Анализ возможностей заданного циклического кода 2.1 Составление порождающей матрицы и матриц проверок Рассмотрим на примере методику построения порождающей матрицы G(15,5) и матрицы проверок H(15,5) для образующего полинома: p(x) = х10 + х9 + х8+ х6 + х5+ х3 +1.
Порождающая матрица в каноническом виде (2) состоит из единичной матрицы в информационных разрядах и матрицы остатков. Она получается путем сложения по модулю 2 определенных строк матрицы (1). Рядом с этой матрицей указаны строки матрицы (1) ,которые надо сложить , чтобы получить соответствующую строку матрицы (2). G(15,5)= Матрица проверок H(15,5) состоит из транспонированной матрицы остатков R и единичной матрицы E:
2.2 Определение минимального кодового расстояния Для определения минимального кодового расстояния d мин (наименьшего из кодовых расстояний в коде) воспользуемся матрицей проверок H(15,5). Минимальное кодовое расстояние равно минимальному количеству столбцов матрицы Н , при сложении по модулю 2 которых получается нулевой столбец. В нашем примере это 1,6,7,12,14 столбцы. Таким образом, d мин =5. Этот код может обнаруживать 4-х кратные ошибки и исправлять 2-х кратные.
2.3 Составление таблицы всех разрешенных кодовых комбинаций и определение их весов. Для получения всех разрешенных комбинаций следует просуммировать по модулю 2 все возможные комбинации строк порождающей матрицы G в каноническом виде. Далее определяем вес каждой кодовой комбинации , то есть количество единиц в ней. Все расчеты выполняем в табл.5.
Таблица №5
2.4 Определение доли необнаруженных ошибок. Из теории циклических кодов известно , что необнаруженная ошибка возникает при появлении полинома ошибки E(x) ,которая имеет вид разрешенной кодовой комбинации. Значит те кодовые комбинации, которые приведены в табл. 5 , и являются полиномами необнаруженной ошибки E(x). Перенесем количество комбинаций с определенным весом в табл.6 и получим распределение числа вариантов необнаруженных ошибок от их кратности. Анализируя это распределение для разных образующих полиномов P(x) ,можно выбрать такой P(x) ,который обеспечит большую помехоустойчивость. Таблица №6
3.Расчет эффективности циклического кода. Эффективность кода - это величина , позволяющая определить способность помехоустойчивого кода обнаруживать ошибки в каналах передачи данных. где :
Следует определить эффективность при передаче данных в канале с независимыми ошибками и в канале с группированием. Необходимые для расчета формулы приводятся : -для канала с независимыми ошибками -для канала с группированием ошибок 4. Определение оптимальной длины блока циклического кода для системы РОС-НП. Следует определить такую длину блока помехоустойчивого кода , при которой обеспечивается максимальная скорость передачи данных и выполняется условие по обеспечению требуемой достоверности:
Формулы для расчета приводятся: Эффективная скорость передачи где
Вероятность необнаруженной ошибки для канала с группированием :
Все расчеты сведены в табл.7, в которой анализируются заданные циклические коды разной длины и избыточности. Таблица №7
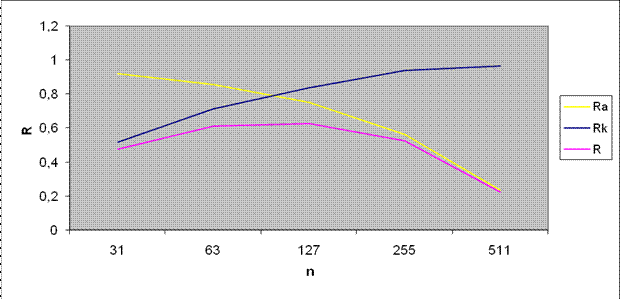
По результатам расчетов строится график зависимости скорости передачи от длины блока и определяется оптимальная длина блока циклического кода. Пример графика показан на Рис. 1
Рис. 1 .
5. Определение максимальной скорости передачи данных по каналу связи с заданными параметрами, при определенном способе модуляции и оптимальном приемнике. В качестве основного параметра характеризующего канал связи, используется вероятность ошибки р0 в зависимости от отношения средних мощностей сигнала и помехи, где последняя представляет собой аддитивный белый шум.
Зависимость ро от h следует представить в виде графика. Пример такого графика для ЧМ приведен на рис. 2 ,где по оси ординат в логарифмическом масштабе откладываются значения вероятности р0 при приеме единичного элемента, а по оси абцисс значения отношения сигнал/помеха h2 в децибелах (дБ).
При построении такого графика для определенного вида модуляции используются формулы, которые приведены в табл.8.
Рис.2. Зависимость вероятности ошибки от отношения сигнал/шум при ЧМ
Таблица 8
Здесь Φ(х) функция Крампа, значения которой приведены в Прил.1. Если при передаче данных задана допустимая вероятность ошибки единичного элемента pдоп, то максимальная скорость Bмакс можно определить с помощью графика из следующего выражения:
Bмакс = Bзад* где Bзад скорость при p0=10-6, h1 - значение при p0=10-6, h2 - значение при p 0доп.
Определение эффективной скорости передачи данных и оптимальной длины блоков для системы РОС-ОЖ. Эффективная скорость Bэфф зависит от состояния канала связи, длины передаваемых блоков и числа служебных разрядов. Блоки данных передаются кадрами, которые состоят nсл1 байт служебных разрядов, r байт проверочных разрядов и k байт информационных разрядов. Обратная связь осуществляется с помощью управляющих кадров, которые состоят из nсл2 байт служебных разрядов. Если в системе передачи данных используются РОС-ОЖ, а модель дискретного канала с независимыми ошибками, то число служебных разрядов nсл будет равно (nсл1+nсл2) байт а эффективная скорость может быть рассчитана по формуле Bэфф= где n=k+r - число байт в принимаемом блоке; k - число информационных байт; r -число проверочных байт; Pко Для определения максимальной эффективной скорости передачи данных и оптимальной длины передаваемых блоков следует построить график зависимости эффективной скорости от длины передаваемых блоков. Если в выражении для Bэфф подставлять k , которое может изменяться от 10 до 300 байт, то получим зависимость Bэфф(k). Характер такого графика изображен на рис. 3 , из анализа которого можно определить максимальную эффективную скорость и оптимальную длину принимаемого блока nопт .Здесь следует предварительно принять r=2 байта.
Рис.3 Зависимость В эф от k
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 320. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
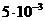
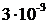
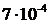
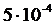
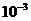
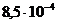
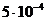
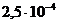
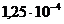
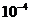

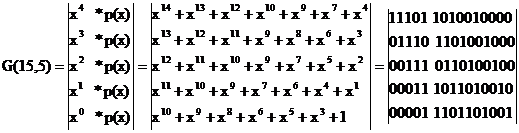 (1)
(1)

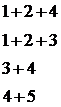
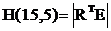
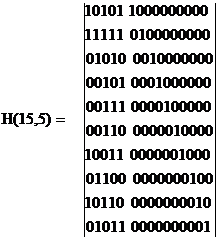
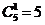
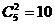
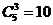
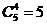
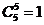
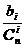
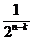
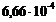
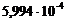
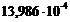
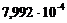
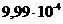
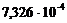
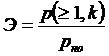 ,
,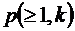 - вероятность ошибки в кодовой комбинации простого кода длины k;
- вероятность ошибки в кодовой комбинации простого кода длины k;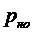 - вероятность необнаруженной ошибки в блоке помехоустойчивого кода.
- вероятность необнаруженной ошибки в блоке помехоустойчивого кода.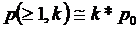
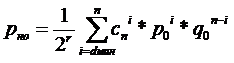
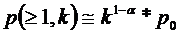
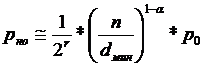
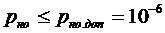
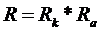 ,
,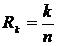 - скорость кода;
- скорость кода;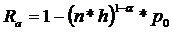 , - скорость алгоритма.
, - скорость алгоритма.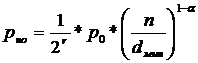
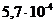
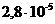
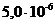
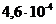
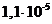
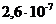
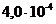
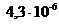
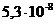
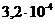
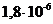
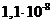
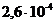
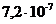
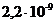
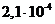
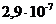
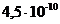
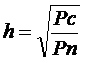
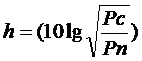 дБ
дБ
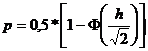
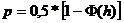
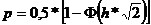
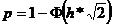
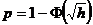
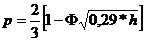
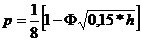
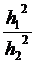
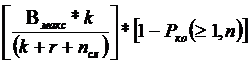
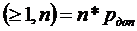 вероятность ошибки в принятом блоке.
вероятность ошибки в принятом блоке.