
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постоянной массы вдоль струиСтр 1 из 2Следующая ⇒ Рис. 3.4. Беспредельная в направлении y плоскопараллельная струя
Установленный выше закон прямолинейного возрастания толщины пограничного слоя в сочетании с универсальностью скоростных профилей приводит к тому, что вдоль любого луча
имеет место
Откуда получаем, что на луче выполняется условие Таким образом, в турбулентном пограничном слое плоскопараллельного затопленного потока лучи, сходящиеся в точке, где толщина пограничного слоя равна Следует отметить, что в начальном участке струи изотахи, построенные для физических Форма изотах в основном участке затопленной струи зависит от способа определения безразмерной скорости. Для безразмерной скорости, полученной путем деления местной скорости на скорость истечения из сопла 
Рис. 3.5. Изотахи безразмерной скорости
Для безразмерной скорости, вычисленной посредством деления местной скорости на величину осевой скорости в соответствующем поперечном сечении Рис. 3.6. Изотахи безразмерной скорости
Данный результат вытекает из того, что указанная безразмерная скорость зависит только от относительного положения точки в поперечном сечении струи
Вследствие линейности закона утолщения струи вышеприведенная зависимость может быть приведена к виду:
чем и доказывается то, что изотахи для безразмерной скорости
3.4 Изменение скорости вдоль оси затопленной струи Статическое давление в струе, как показывают опыты, практически неизменно и равно давлению в окружающем пространстве. Благодаря этому полный импульс секундной массы воздуха во всех сечениях струи должен оставаться одним и тем же: где
Для струи круглого сечения условие постоянства импульса можно записать следующим образом: где Вследствие универсальности скоростных профилей безразмерная скорость
Отсюда
В результате из равенства (1), получаем, что скорость в центре сечения осесимметричной затопленной струи обратно пропорциональна расстоянию от полюса: Для плоскопараллельной затопленной струи постоянство импульса приводит к соотношению:
где b - полутолщина сечения струи. Вследствие универсальности профилей скорости
Поэтому закон падения скорости вдоль оси плоскопараллельной струи имеет следующий вид: Константы пропорциональности в выражениях (2) и (4) определяются значениями интегралов из выражений (1) и (3), для вычисления которых нужно располагать законами распределения скорости в поперечных сечениях струй. В силу универсальности профилей скорости для этого достаточно определить распределение скоростей экспериментальным путем хотя бы в одном сечении основного участка струи. Недостатком выражений (2) и (4) является то, что расстояния
3.5 Перенос тепла в затопленной струе В инженерной практике часто приходится иметь дело с затопленной струей, температура в которой отличается от окружающей температуры. Решение задачи о переносе тепла из покоящегося воздуха в струю (и обратно) возможно лишь, после того как станут, известны законы изменения температуры вдоль струи и в ее поперечных сечениях. Введем в рассмотрение избыточные температуры: а) разность между температурой в данной точке струи и в окружающем пространстве:
б) разность между температурой на оси струи и в окружающем пространстве:
в) разность между температурой в начальном сечении струи (в устье насадка) и в окружающем пространстве:
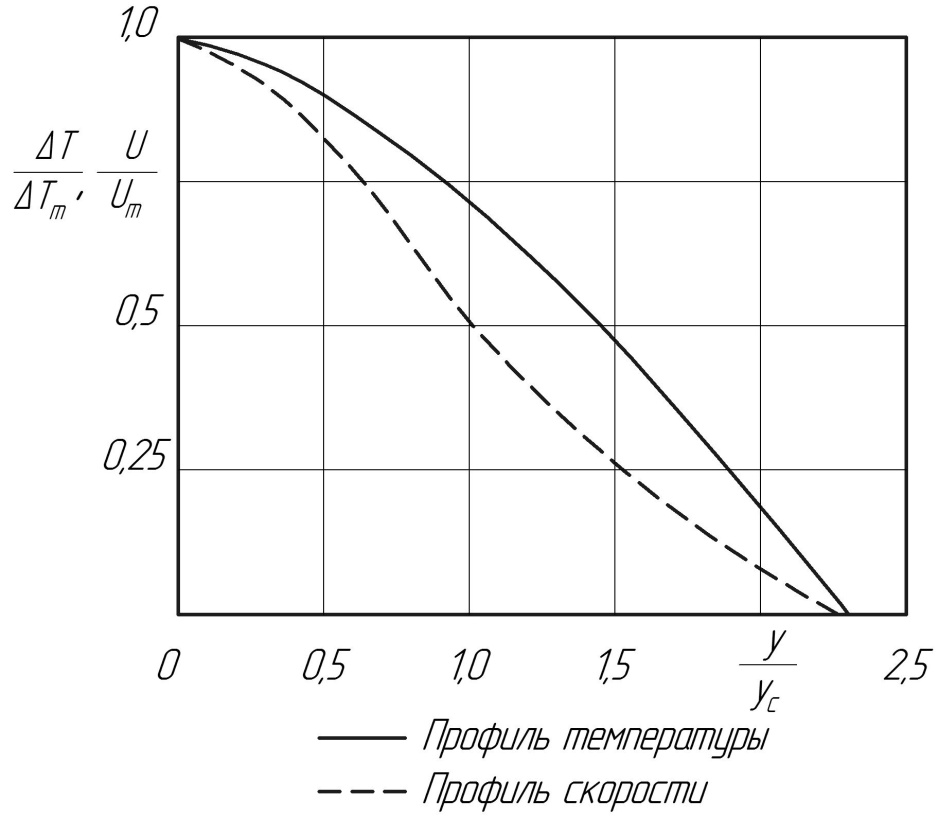
Характер распределения избыточных значений температуры в затопленной струе, как показывают опыты, аналогичен характеру распределения скорости. На рисунке 3.7 нанесены безразмерные избыточные значения температуры в координатах Помимо значений температуры на рис. 3.7 нанесены, снятые в тех же сечениях скоростные поля. Очевидным является, что экспериментальные кривые безразмерной скорости и избыточной безразмерной температуры, полученные в одном и том же поперечном сечении затопленной струи, не совпадают.
Рис. 3.7. Профили безразмерной температуры и Скорости в сечении струи
Закон распределения температуры вдоль оси основного участка струи можно установить тем же методом, что и закон скоростей, с той лишь разницей, что вместо постоянства импульса надо использовать постоянство энтальпии струи. Постоянство энтальпии свободной струи, подсчитанной по избыточным значениям температуры, выражается следующим соотношением: Для струи круглого сечения получим: Отметим, что в различных поперечных сечениях струи, линии безразмерных изотерм, аналогично изотахам, являются прямолинейными лучами, пересекающимися в полюсе струи: где
Из условия (7) вытекает, что интеграл в соотношении (6) является постоянной величиной. Отсюда, учитывая зависимость (2), получим закон падения избыточной температуры вдоль оси струи круглого сечения: Зависимость (8) совпадает с опытными данными. Докажем теорему о связи между средними температурами и средними скоростями. Из постоянства импульса в струе следует, что произведение секундной массы, протекающей через произвольное сечение струи, на некоторую среднюю скорость является постоянной величиной: В свою очередь, постоянство энтальпии указывает на то, что произведение массового расхода на среднюю избыточную температуру также не изменяется с переходом от сечения к сечения: Сравнивая между собой условия (9) и (10), обнаруживаем, что падение средней температуры вдоль свободной струи подчиняется тому же закону, что и падение средней скорости: Необходимо отметить, что условие (11), характеризующее соотношение средних величин, выполняется, несмотря на то, что температурные и скоростные профили в затопленной струе не подобны. Равенство (11) справедливо только для среднеквадратичной скорости, то есть в том случае, когда последняя получена путем осреднения по расходу:
3.6 Диффузия примесей в затопленной струе Диффузия всякого рода примесей, находящихся иногда в струе во взвешенном состоянии, имеет много общего с распространением тепла. На рис. 3.8 приведены профили безразмерной весовой концентрации углекислого газа, полученные Г.Н. Абрамовичем при экспериментальном исследовании основного участка плоскопараллельной струи углекислого газа, вытекающей в неподвижный чистый воздух:
где
Рис. 3.8. Профили безразмерной температуры, скорости и весовой концентрации СО2 в сечении струи
В тех случая, когда примесь имеется и в окружающей среде, целесообразно ввести в рассмотрение понятие избыточной концентрации -
Условия постоянства избыточного содержания примеси, а также афинность полей концентрации в поперечных сечениях дают возможность найти закон изменения концентрации примеси по оси струи. В основном участке осесимметричной струи при условии сохранения избыточного содержания примеси, имеем:
где
то есть избыточная концентрация примеси на оси основного участка затопленной струи круглого сечения обратно пропорциональна расстоянию от полюса струи. В случае плоской струи постоянство избыточного содержания примеси выражается равенства: Следовательно, аналогично предыдущим случаям можно написать, что избыточная концентрация примеси по оси основного участка плоскопараллельной затопленной струи изменяется обратно пропорционально корню квадратному из рассеяния до полюса струи:
Исходя из того же условия сохранения избыточного содержания примеси, получается, что безразмерное значение средней по расходу концентрации примеси равно безразмерному значению средней по расходу скорости, которая в свою очередь, как показано в предыдущем пункте, равно безразмерному значению средней избыточной температуры:
где Итак, поля безразмерных значений избыточной концентрации примеси и избыточной температуры совпадают между собой; это объясняется тем, что механизм переноса тепла и примесей в турбулентном потоке один и тот же.
3.7 Теория "пути смешения" Прандтля
В 1925 году Л. Прандтль предложил простую и наглядную модель переноса субстанции между слоями осредненного турбулентного движения. Модель Прандтля заключается в допущении о том, что вихревая масса во все время перемещения из начального слоя в конечный, сохраняет свое отличие в импульсе и только в момент смешения сразу теряет свою индивидуальность, вызвав тем самым в этом конечном слое возмущение в осредненной скорости. Это возмущение принимается пропорциональным расстоянию между начальным и конечным слоями Эта центральная формула теории Прандтля приводит к выражению касательной, составляющей напряжения в случае рассматриваемого простейшего прямолинейного сдвигового движения:
Если условится понимать под
Единственную остающуюся здесь неопределенной величину l Прандтль назвал путем смешения. Чтобы не делать оговорки о знаке Сущность теории свободной турбулентности Прандтля состоит в следующем. Ввиду отсутствия (для случая струи) стенок, вблизи которых путь смешения обычно уменьшается, предполагается, что в поперечном направлении путь смешения не изменяется: Итак, если струя распространяется в направлении оси где Исходя из дифференциального уравнения теплопроводности для слоя потока жидкости, можно найти закон распределения температуры в струе: В процессе турбулентного перемешивания частицы жидкости переносят с места на место содержащиеся в них тепло и примеси. Температура и концентрация примесей являются однотипными скалярными параметрами жидких частиц. Поэтому распределение примесей в турбулентной струе должно подчиняться тем же законам, что и распределение температур:
3.8 Общие зависимости, характеризующие осесимметричную струю Уравнение движения (22), теплообмена (23), и диффузии примеси (24) получены с помощью теории свободной турбулентности Прандтля, основывающейся на предположении об одинаковости механизмов турбулентного переноса количества движения, тепла и примеси. Решение этих уравнений дает возможность построить картину течения жидкости тепловых и диффузионных процессов в струе. На рис. 3.9 схематически изображена свободная струя, разделенная на начальный и основной участки. Поместим начало координат в полюс струи.
Рис. 3.9. Свободная струя, разделенная на начальный и основной участки
Для того чтобы исключить из уравнения движения (22) экспериментальную константу, полагаем: Выберем систему координат: где Основываясь на свойствах струи, рассмотренных ранее, можно вывести: 1) Осевая скорость для основного участка струи круглого сечения: 2) В переходном сечении струи, от которого начинается основной участок, осевая скорость равна скорости истечения. откуда найдем абсциссу (безразмерное расстояние от полюса) переходного сечения струи: 3) Для вычисления геометрических параметров начального участка струи используют формулу (29), а безразмерная ордината границы основного участка
длину начального участка: коэффициент структуры потока в начальном участке: ординату внутренней границы поперечного слоя: и ординату внешней границы начального участка струи:
4) Закон падения температуры вдоль оси основного участка турбулентной струи круглого сечения записывается в виде:
5) Профили концентрации примесей в струе: где
4. Расчет затопленной струи несжимаемой жидкости По вышеприведенным формулам произведем расчет осесимметричной струи с начальными параметрами:
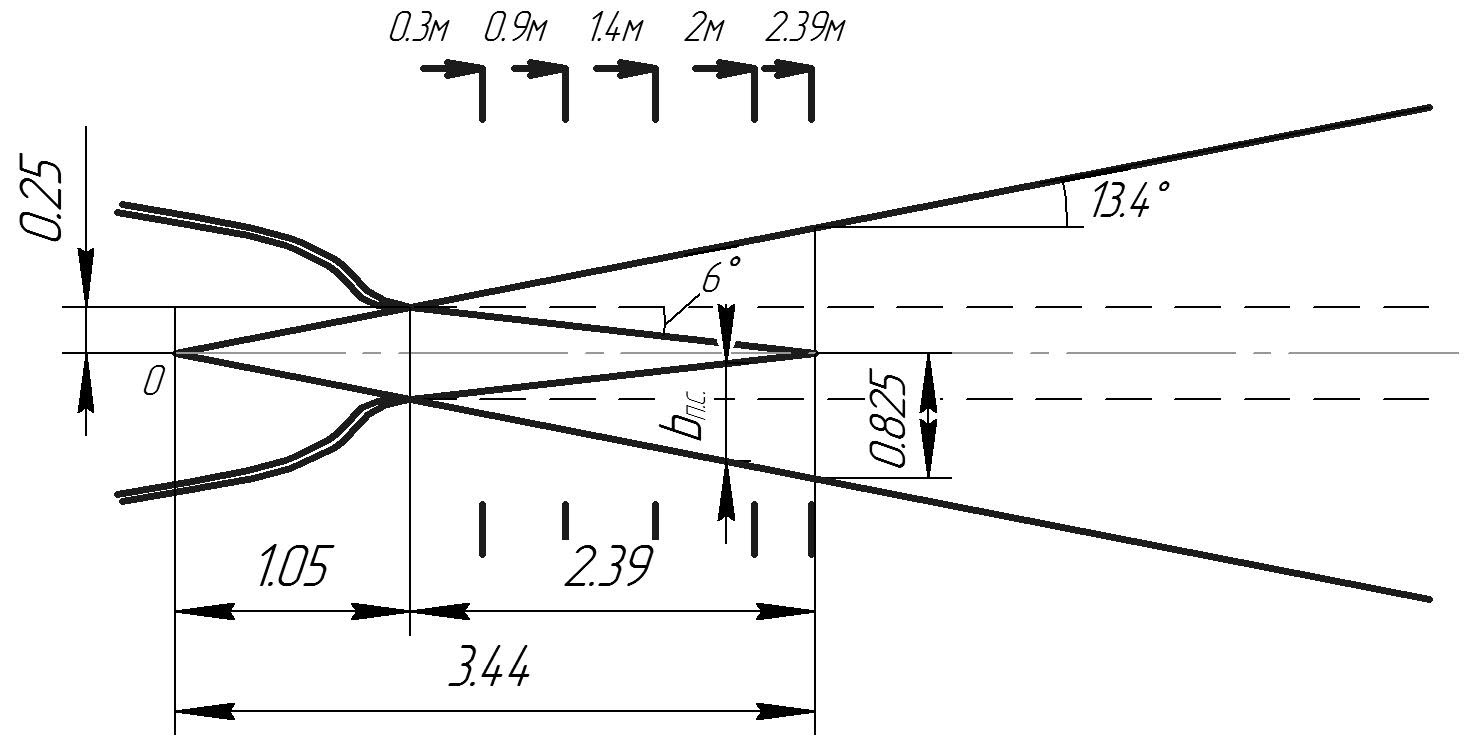
Схема осесимметричной затопленной струи для рассматриваемого случая выглядит следующим образом (рис. 4.1):
Рис. 4.1. Схема осесимметричной затопленной струи
Найдем полюс струи, который лежит глубже начального сечения струи на расстоянии от него, равном:
где Отсюда, подставляя начальные данные струи, в рассматриваемом случае при
Проведем через полюс струи и через выходную кромку сопла лучи внешней границы струи. Тангенс угла расширения внешней границы равен:
При
Отсюда угол
Далее определим местоположение переходного сечения струи:
Подставляя численные значения, найдем:
Радиус переходного сечения является постоянной величиной и не зависит от структуры струи. Для его определения используют соотношение:
Отсюда радиус переходного сечения в нашем случае:
Соединим центр переходного сечения с кромкой сопла и таким образом получим границу ядра постоянных скоростей Тангенс угла сужения границы ядра постоянных скоростей равен:
При
Отсюда угол Угол расширения пограничного слоя начального участка струи
Ширина пограничного слоя в произвольном сечении начального участка определяется зависимостью:
Отсюда выражаем
Таким образом, ширина пограничного слоя зависит от расстояния
Полный радиус струи на заданном расстоянии
Отсюда выражая
Аналогично предыдущему случаю зададим ряд значений
Определим осевую скорость на различных участках струи. В переходном сечении струи, т.е. для начального участка, осевая скорость равна скорости истечения:
Учитывая, что по условию
Длина начального участка определяется выражением:
Выразим отсюда
Подставив численные значения, получим:
Безразмерная осевая скорость для основного участка струи круглого сечения определяется выражением:
Перепишем это равенство с учетом, что
Очевидно, что значение скорости
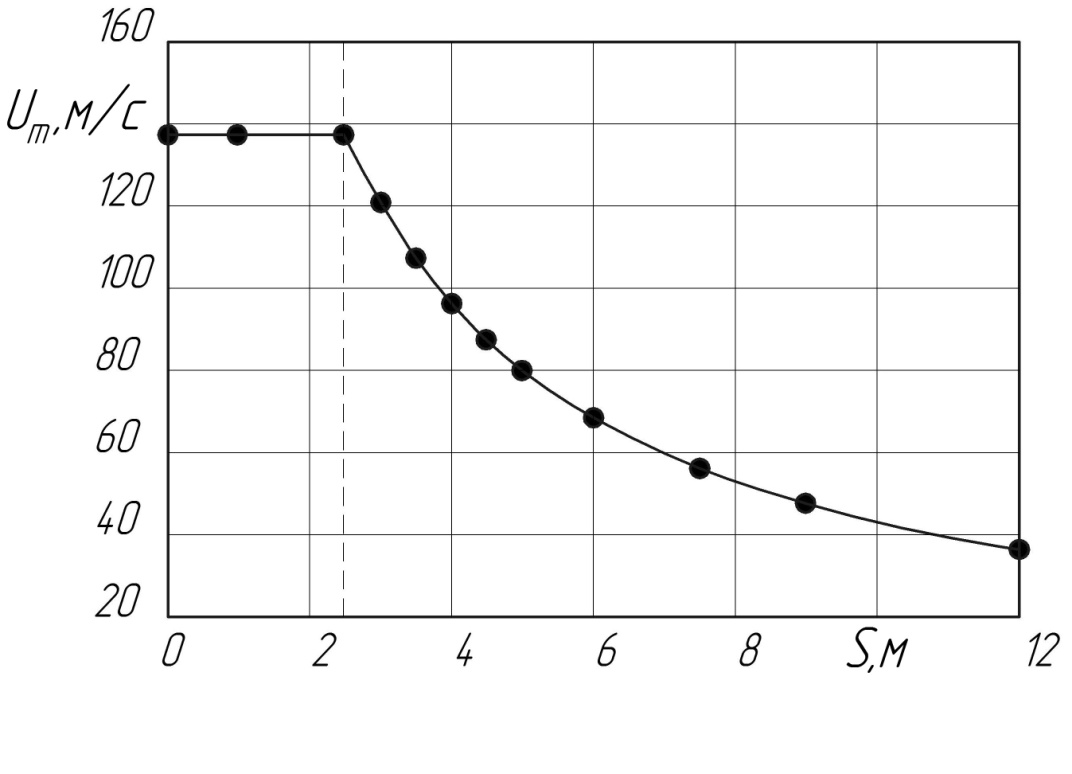
Для исследуемого случая график изменения осевой скорости вдоль всей свободной струи приведен на рис. 4.2:
Рис. 4.2. Изменение скорости вдоль оси струи
Запишем закон падения температуры вдоль оси основного участка турбулентной струи круглого сечения:
В представленной зависимости Подставим численное значение
В ядре постоянных скоростей начального участка следует полагать температуру постоянной и равной температуре истечения
По полученным данным построим кривую падения температуры вдоль оси струи при значении избыточной температуры в начале струи
Рис. 4.3. Кривая падения температуры вдоль оси струи
По результатам расчета получилось, что в начале основного участка струи ( Полученное противоречие, не имеющее большого практического значения, можно устранить введением особого переходного участка струи, который расположится между начальным и основным участками. График тогда будет выглядеть следующим образом:
Рис. 4.4. Кривая падения температуры вдоль оси струи с учетом длины переходного участка
Секундное количество воздуха, протекающее сквозь поперечное сечение основного участка струи, равно:
Расход воздуха в долях от его величины в начальном сечении выражается зависимостью:
В представленном выражении отношение:
А интеграл:
Тогда с учетом этого после преобразований формула безразмерной величины расхода воздуха в основном участке осесимметричной струи примет вид: Расход воздуха на начальном участке струи может быть представлен в виде суммы расходов ядра постоянных скоростей и пограничного слоя:
где
Вычисление интегралов по таблицам [2] приводит к следующим значениям:
Заменяя интегралы их численными значениями, получаем формулу для безразмерного значения расхода воздуха на начальном участке осесимметричной струи:
Рассмотрим изменение расхода по длине струи (в долях от его величины в начальном сечении) в исследуемом нами случае, т.е. при
Рассчитаем значение безразмерного расхода на основном участке струи, при различных значениях
Проделав расчет для переходного сечения струи
Используя полученные результаты, представим графически изменение безразмерного расхода по длине струи (рис. 4.5):
Рис. 4.5. Изменение безразмерного расхода по длине струи
Таким образом, расход сквозь поперечное сечение струи возрастает с увеличением расстояния сечения от сопла. Безразмерный запас энергии на основном участке осесимметричной струи измеряется величиной:
По таблицам [2] находим значение интеграла:
Отношение скоростей
Учитывая два вышеприведенных равенства, преобразуем выражение для определения безразмерного запаса энергии на основном участке осесимметричной струи. В конечном итоге имеем: Безразмерный запас энергии на начальном участке определяется выражением:
Определенные интегралы вычисляем по таблицам [2]:
Заменив интегралы их численными значениями, и преобразовав полученное выражение, находим формулу безразмерного запаса энергии на начальном участке осесимметричной струи:
Рассчитаем значение безразмерного запаса энергии на начальном участке осесимметричной струи, при различных значениях
На основном участке струи определяем значение безразмерного запаса энергии используя формулу (39):
По полученным значениям построим график изменения запаса энергии в струе:
Рис. 4.6. Изменение безразмерного запаса энергии вдоль струи
Значение безразмерной средней арифметической скорости в поперечном сечении струи равно отношению расхода к площади сечения: На основном участке струи безразмерная величина средней скорости оказывается константой, что объясняется подобием скоростных профилей в различных сечениях основного участка струи: Помимо полученной выше безразмерной средней скорости имеет большое значения безразмерная среднеквадратичная скорость, которая представляет собой отношение импульса, протекающего в единицу времени сквозь поперечное сечение струи, к массовому расходу жидкости в том же поперечном сечении. Вследствие постоянства импульса струи его величина равна:
тогда как массовый расход составляет:
Отсюда получаем, что выражение для среднеквадратичной скорости имеет вид:
В безразмерном виде это уравнение выглядит следующим образом:
Таким образом, безразмерная средняя квадратичная скорость на основном участке струи круглого сечения составляет: На начальном участке струи величина безразмерной средней арифметической скорости равна: а безразмерная средняя квадратичная скорость выражается следующим образом:
Рассчитаем значения средней арифметической и средней квадратичной безразмерных скоростей на начальном участке осесимметричной струи, при различных значениях
На основном участке безразмерные средняя арифметическая и средняя квадратичная скорости постоянны и определяются выражениями (42) и (43) соответственно:
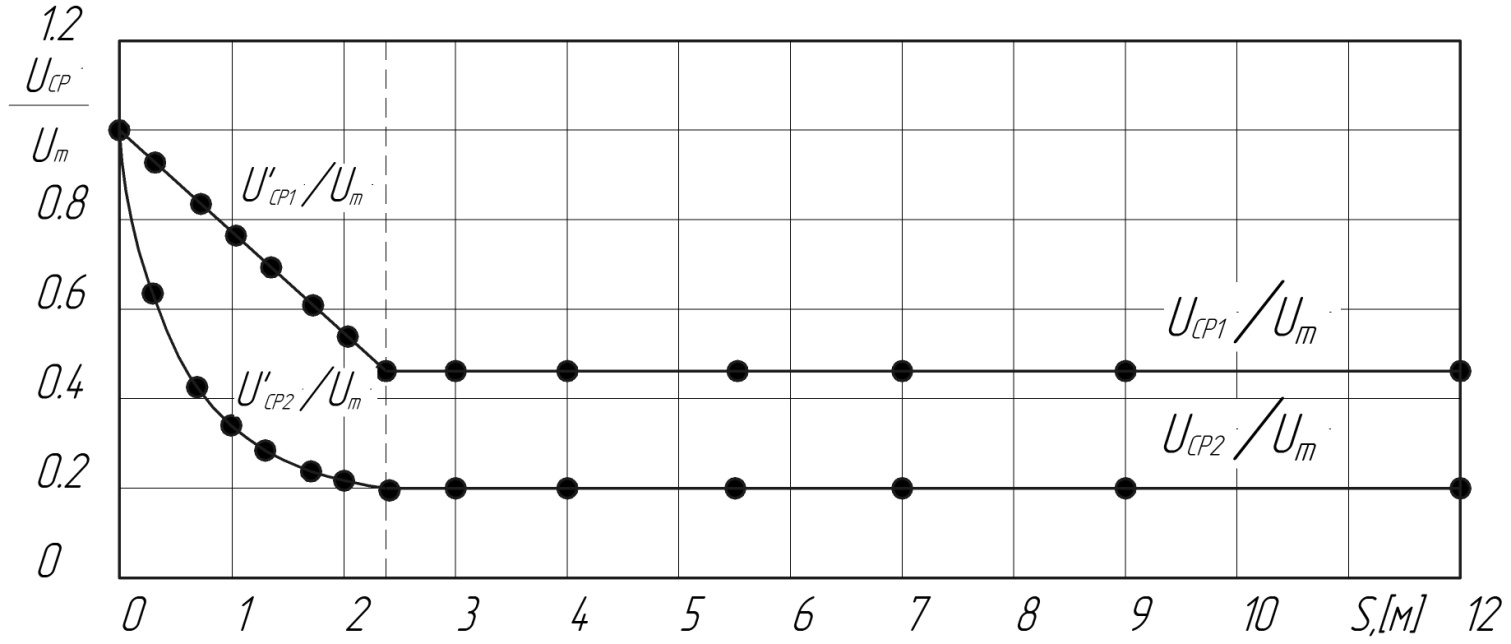
По рассчитанным значениям построим график, отражающий изменение средних скоростей по длине струи.
Рис. 4.7. Изменение безразмерных средних скоростей по длине струи
Воспользуемся теоремой о равенстве безразмерных значений средней температуры и средней квадратичной скорости в произвольном сечении произвольного участка струи:
Или, подставив известные значения скоростей, имеем: Получили безразмерное значение средней температуры в поперечном сечении основного участка струи.
Тот же закон получается и для средних концентраций примесей в поперечном сечении основного участка струи: где Границы ядра первоначальной массы струи могут быть определены из условия постоянства расхода в ядре ( Безразмерный расход на основном участке ядра постоянной массы равен:
Введем обозначение интеграла:
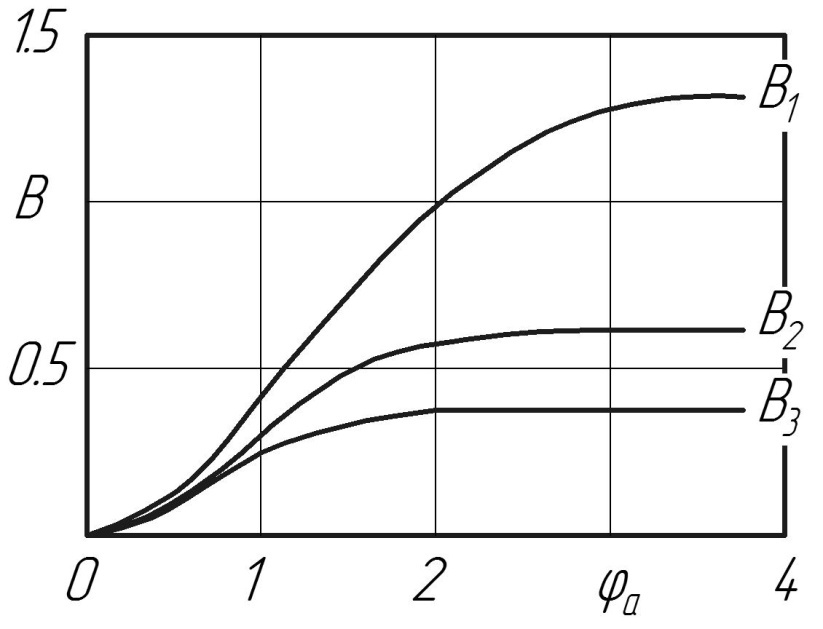
Учитывая, что Выражение (50) дает возможность вычислить безразмерный радиус ядра постоянной массы в области основного участка круглой струи: Вычисление отношения 1) По заданному значению 2) Из рис. 4.8 по зависимости В1= 3) По формуле (51) находят
Рис. 4.8. Зависимости В=
Вычислим радиус ядра
Из графика по вычисленной величине
Аналогичным образом рассчитаем остальные значения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 254. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
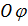 , проведенного из начала координат (последнее совмещается с точкой
, проведенного из начала координат (последнее совмещается с точкой 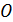 , где толщина пограничного слоя равна нулю), скорость остается постоянной. Исходя из этого вытекает равенство скоростей в сходственных точках потока, то есть при
, где толщина пограничного слоя равна нулю), скорость остается постоянной. Исходя из этого вытекает равенство скоростей в сходственных точках потока, то есть при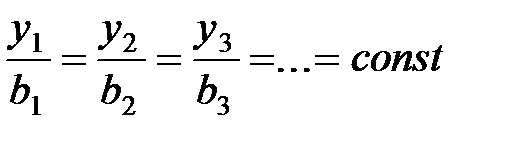
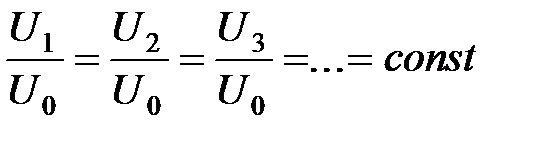 .
.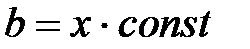
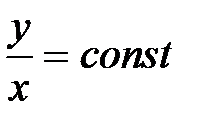
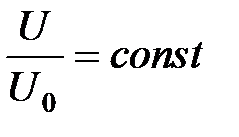 .
. 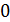 , представляют собой изотахи (линии равных значений скорости). Данный результат относится не только к плоскопараллельному потоку, но в равной мере и к пограничному слою в начальном участке струи круглого сечения, поскольку опыты показывают, что и в этом случае поля скорости универсальны. Началом координат для изотах пограничного слоя в начальном участке струи служит выходная кромка сопла (при равномерном поле скорости в начальном сечении струи).
, представляют собой изотахи (линии равных значений скорости). Данный результат относится не только к плоскопараллельному потоку, но в равной мере и к пограничному слою в начальном участке струи круглого сечения, поскольку опыты показывают, что и в этом случае поля скорости универсальны. Началом координат для изотах пограничного слоя в начальном участке струи служит выходная кромка сопла (при равномерном поле скорости в начальном сечении струи).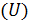 и для безразмерных
и для безразмерных 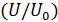 скоростей, совпадают, так как в ядре скорость
скоростей, совпадают, так как в ядре скорость 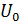 по длине не меняется.
по длине не меняется.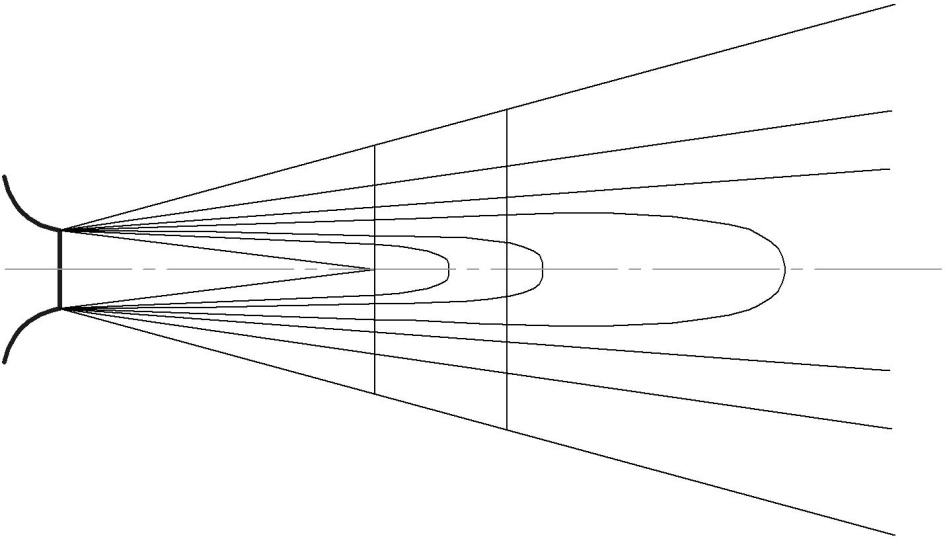
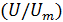 изотахи основного участка представляют собой прямые линии, сходящиеся в полюсе струи (рис. 3.6).
изотахи основного участка представляют собой прямые линии, сходящиеся в полюсе струи (рис. 3.6).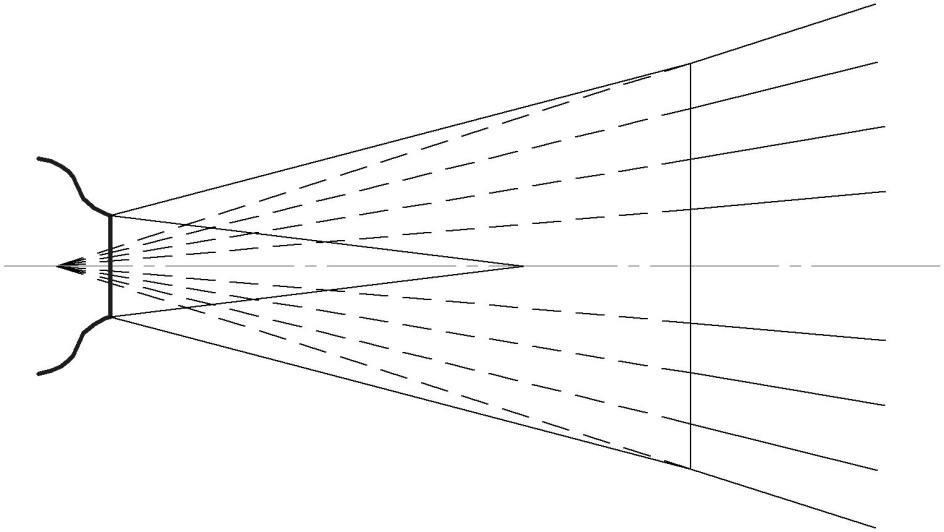
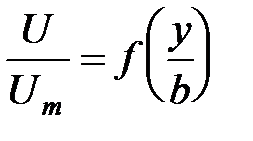 .
. 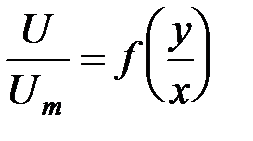 ,
,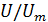 являются лучами, которые пересекаются в полюсе струи. Прямолинейность изотах для безразмерной скорости
являются лучами, которые пересекаются в полюсе струи. Прямолинейность изотах для безразмерной скорости 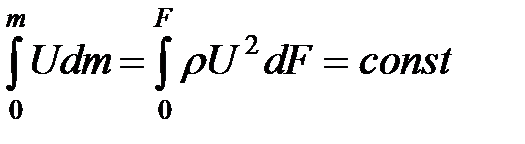 ,
, 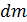 - масса, протекающая в единицу времени через элемент поперечного сечения струи;
- масса, протекающая в единицу времени через элемент поперечного сечения струи; 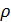 - плотность воздуха;
- плотность воздуха; 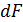 - площадь элемента сечения струи.
- площадь элемента сечения струи.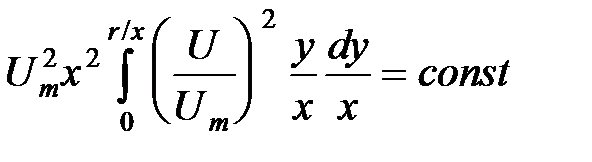 , (1)
, (1)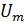 - скорость в центре данного сечения струи;
- скорость в центре данного сечения струи; 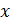 - расстояние от данного сечения до полюса струи;
- расстояние от данного сечения до полюса струи; 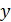 - текущий радиус; r - радиус внешней границы рассматриваемого сечения струи.
- текущий радиус; r - радиус внешней границы рассматриваемого сечения струи.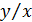 , проведенного из полюса струи через эту точку:
, проведенного из полюса струи через эту точку: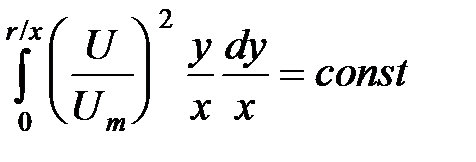 .
.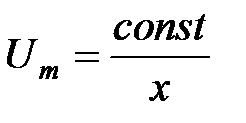 . (2)
. (2)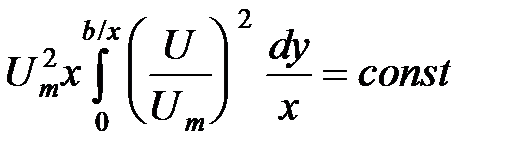 , (3)
, (3)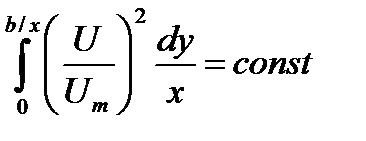 .
.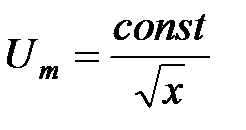 . (4)
. (4)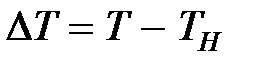 ,
,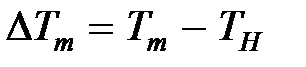 ,
,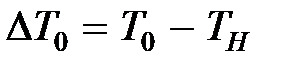 .
.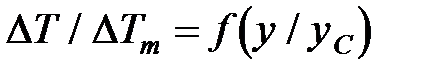 , полученные С.Б. Старком в различных поперечных сечениях основного участка осесимметричной воздушной струи, вытекающей в неподвижный воздух. В опытах Старка использовалось сопло диаметром
, полученные С.Б. Старком в различных поперечных сечениях основного участка осесимметричной воздушной струи, вытекающей в неподвижный воздух. В опытах Старка использовалось сопло диаметром 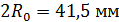 , скорость истечения струи составляла
, скорость истечения струи составляла 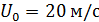 и начальная избыточная температура в струе
и начальная избыточная температура в струе 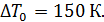
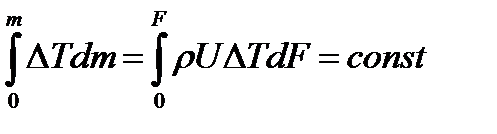 . (5)
. (5)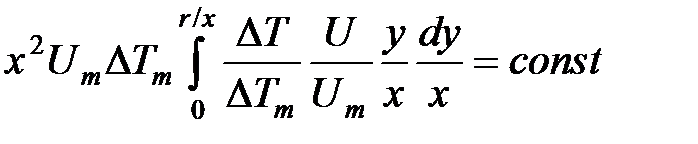 . (6)
. (6)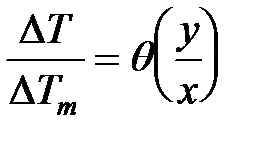 , (7)
, (7) 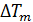 .
.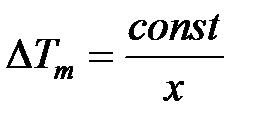 . (8)
. (8)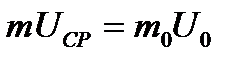 , то есть
, то есть 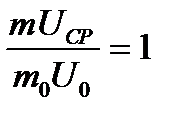 . (9)
. (9)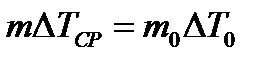 , то есть
, то есть 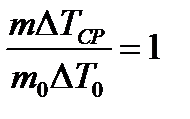 . (10)
. (10)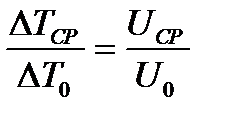 . (11)
. (11) 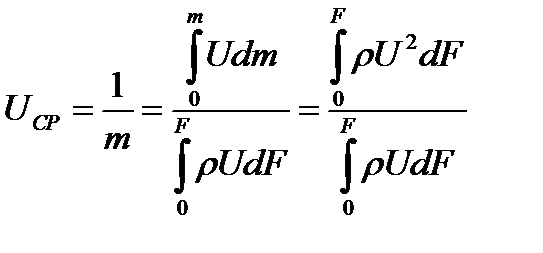 ;
; 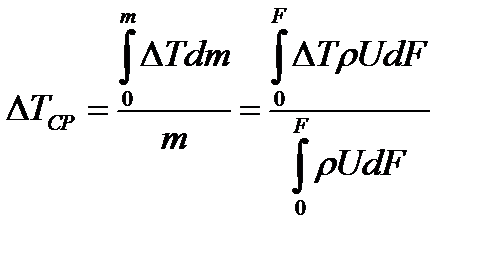 .
.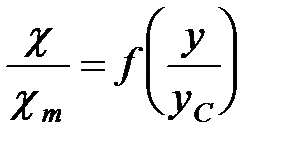 ,
,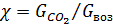 - весовая концентрация, то есть отношение весового содержания углекислого газа к весовому содержанию воздуха в единице объема в произвольной точке поперечного сечения струи;
- весовая концентрация, то есть отношение весового содержания углекислого газа к весовому содержанию воздуха в единице объема в произвольной точке поперечного сечения струи; 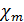 - весовая концентрация
- весовая концентрация  на оси струи;
на оси струи; 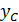 - расстояние от оси струи до точки, в которой избыточная скорость вдвое меньше чем на оси.
- расстояние от оси струи до точки, в которой избыточная скорость вдвое меньше чем на оси.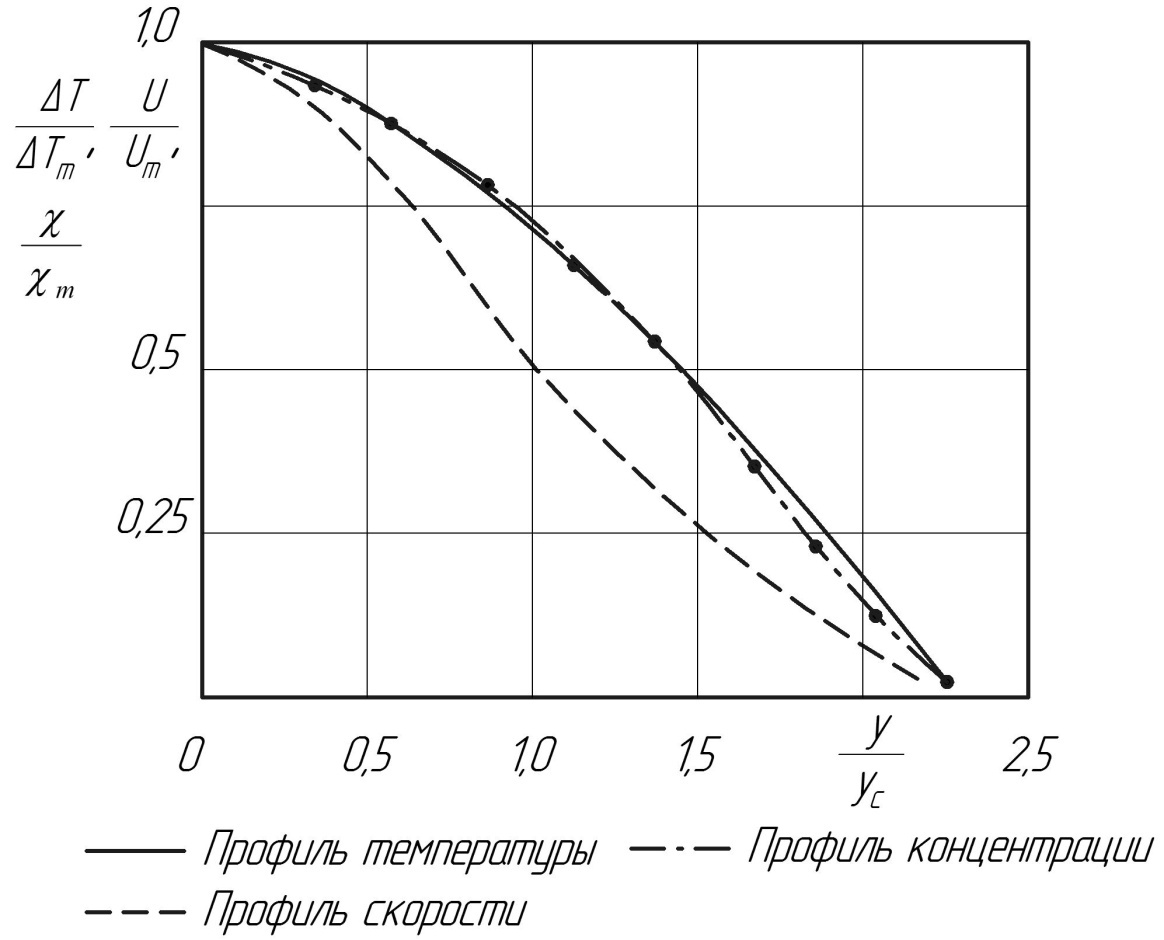
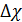 , означающую разность между местной концентрацией примеси в струе и концентрацией той же примеси вне струи. Очевидно, что избыточное содержание примеси, равно как и избыточное значение энтальпии, одинаково в различных поперечных сечениях струи:
, означающую разность между местной концентрацией примеси в струе и концентрацией той же примеси вне струи. Очевидно, что избыточное содержание примеси, равно как и избыточное значение энтальпии, одинаково в различных поперечных сечениях струи: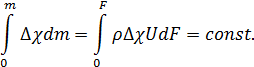
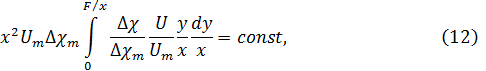
 - избыточная концентрация примеси струи. Ввиду универсальности законов распределения скорости и концентрации в поперечных сечениях струи интеграл, стоящий в левой части равенства (12) есть величина постоянная, поэтому с учетом (2) получаем:
- избыточная концентрация примеси струи. Ввиду универсальности законов распределения скорости и концентрации в поперечных сечениях струи интеграл, стоящий в левой части равенства (12) есть величина постоянная, поэтому с учетом (2) получаем:
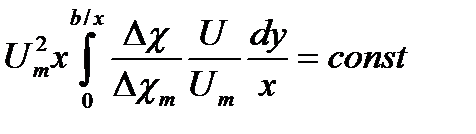 . (14)
. (14)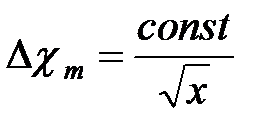 . (15)
. (15)
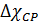 - разность между средним по расходу значением концентрации
- разность между средним по расходу значением концентрации 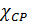 в данном сечении струи и концентрацией той же примеси в окружающей среде
в данном сечении струи и концентрацией той же примеси в окружающей среде 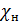 .
.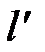 и величине разности между осредненными скоростями в этих слоях
и величине разности между осредненными скоростями в этих слоях 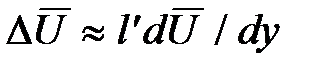 . По мысли Прандтля, данное возмущение в осредненной скорости слоя является причиной возникновения в нем пульсационной скорости с проекциями
. По мысли Прандтля, данное возмущение в осредненной скорости слоя является причиной возникновения в нем пульсационной скорости с проекциями 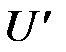 и
и 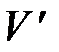 :
: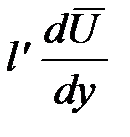 ;
; 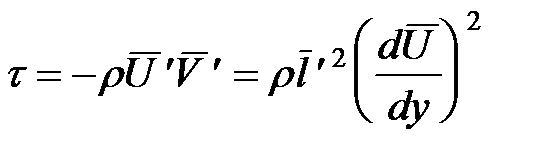 .
.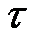 напряжение трения, приложенное к верхней границе слоя со стороны области больших скоростей (
напряжение трения, приложенное к верхней границе слоя со стороны области больших скоростей ( 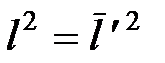 , то предыдущее выражение для
, то предыдущее выражение для 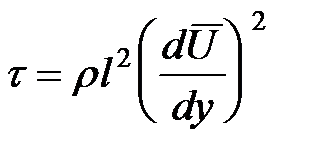 . (18)
. (18)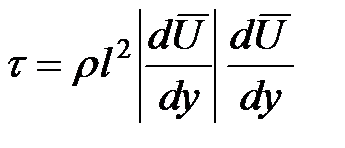 . (19)
. (19)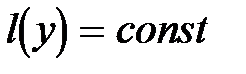 . (20)
. (20)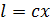 , что при подстановки в (19) дает:
, что при подстановки в (19) дает: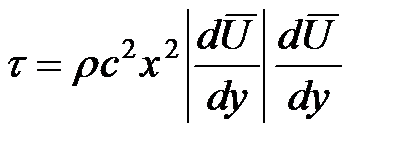 , (21)
, (21)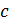 - единственная эмпирическая постоянная теории свободной турбулентности Прандтля. Используя выражение (21), можно получить уравнение двухмерного движения из теории свободной турбулентности Прандтля:
- единственная эмпирическая постоянная теории свободной турбулентности Прандтля. Используя выражение (21), можно получить уравнение двухмерного движения из теории свободной турбулентности Прандтля: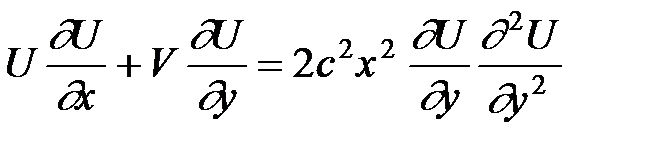 . (22)
. (22)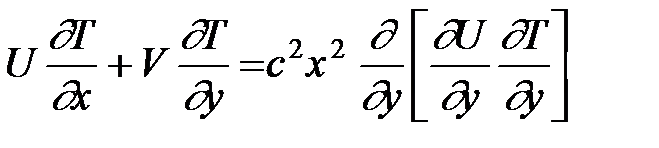 . (23)
. (23)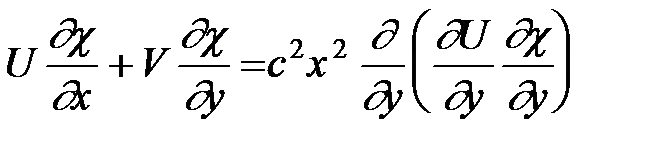 . (24)
. (24)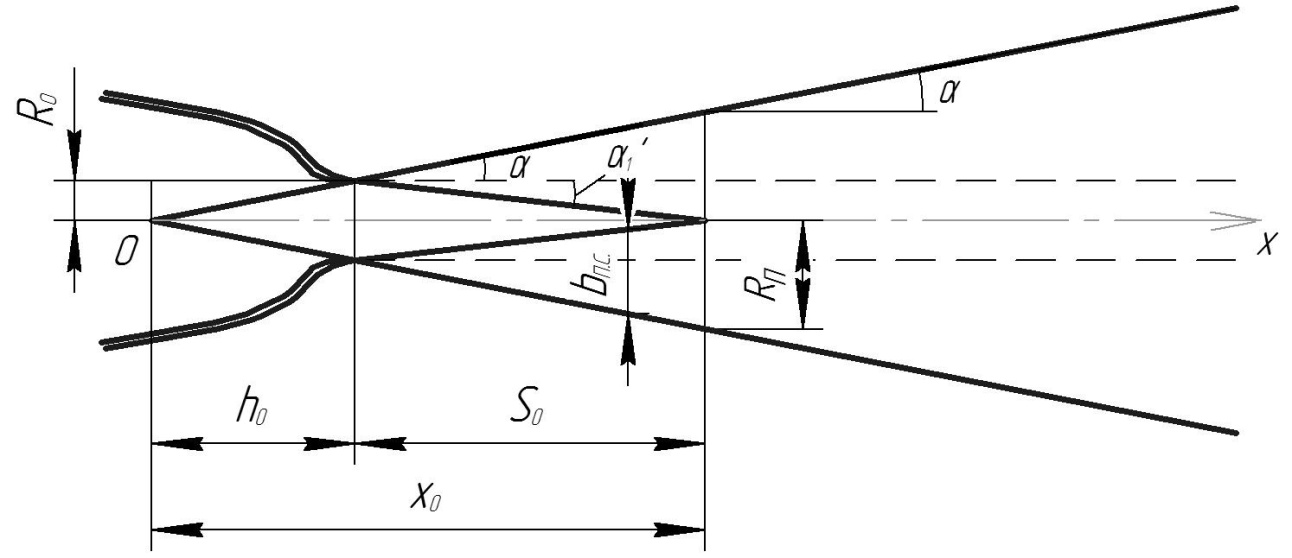
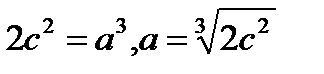 . (25)
. (25)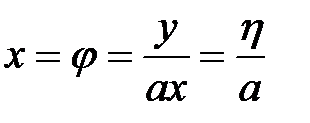 , (26)
, (26)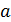 - эмпирическая константа, характеризующая структуру струи. По экспериментальным данным для осесимметричной струи а » 0,07.
- эмпирическая константа, характеризующая структуру струи. По экспериментальным данным для осесимметричной струи а » 0,07.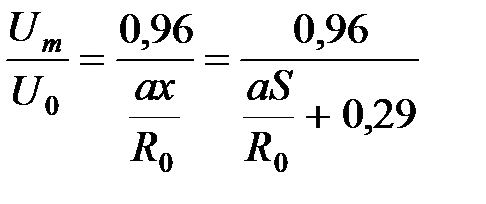 . (27)
. (27)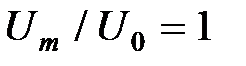 , (28)
, (28)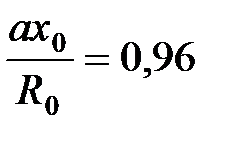 . (29)
. (29) =3,4. Отсюда находят глубину полюса:
=3,4. Отсюда находят глубину полюса: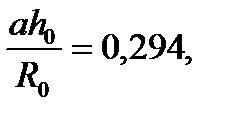 (30)
(30)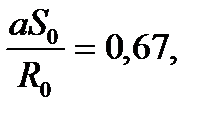 (31)
(31)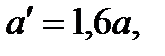 (32)
(32)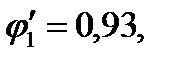 (33)
(33)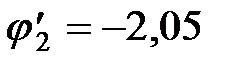 . (34)
. (34)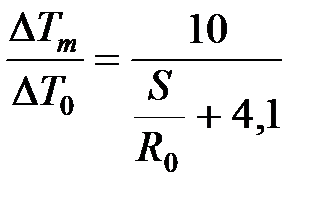 . (35)
. (35)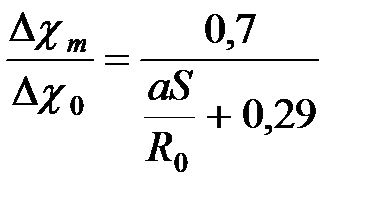 . (36)
. (36)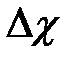 - избыточная концентрация точки струи;
- избыточная концентрация точки струи; 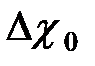 – избыточная концентрация в начальном сечении струи;
– избыточная концентрация в начальном сечении струи;  – избыточная концентрация на оси соответствующего поперечного сечения струи.
– избыточная концентрация на оси соответствующего поперечного сечения струи.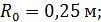
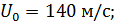
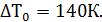
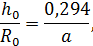
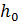 - глубина полюса,
- глубина полюса, 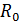 - радиус начального сечения струи,
- радиус начального сечения струи, 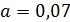 .
.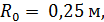 получим глубину полюса:
получим глубину полюса: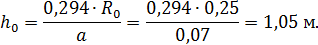
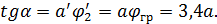
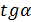 будет равно:
будет равно: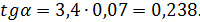
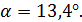
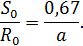
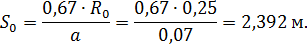
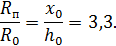
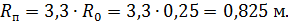
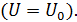
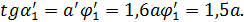
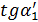 будет равно:
будет равно: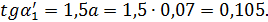
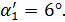
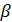 состоит из суммы углов
состоит из суммы углов 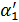 и
и 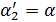 :
: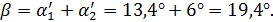
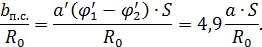
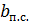 :
: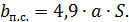
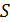 . Поэтому зададим ряд значений
. Поэтому зададим ряд значений 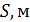
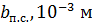
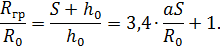
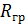 , получим:
, получим: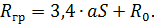
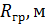
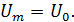
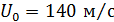 , осевая скорость на начальном участке истечения равна:
, осевая скорость на начальном участке истечения равна: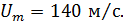
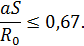
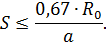
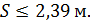
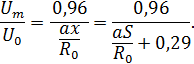
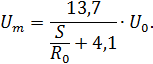
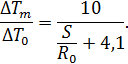
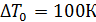 - избыточная температура в начале исследуемой струи, заданная по условию.
- избыточная температура в начале исследуемой струи, заданная по условию.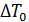 , выразив при этом
, выразив при этом 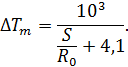
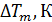
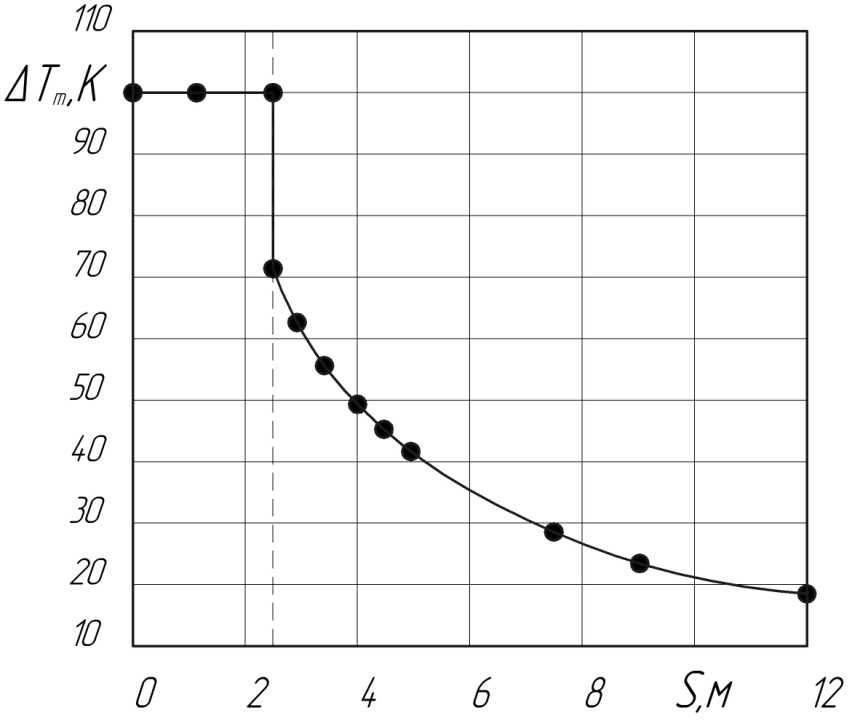
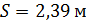 ) осевая температура
) осевая температура 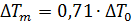 ). Это свидетельствует о том, что переходное сечение для профилей температуры расположено несколько ближе к началу струи, чем переходное сечение для профилей скорости.
). Это свидетельствует о том, что переходное сечение для профилей температуры расположено несколько ближе к началу струи, чем переходное сечение для профилей скорости.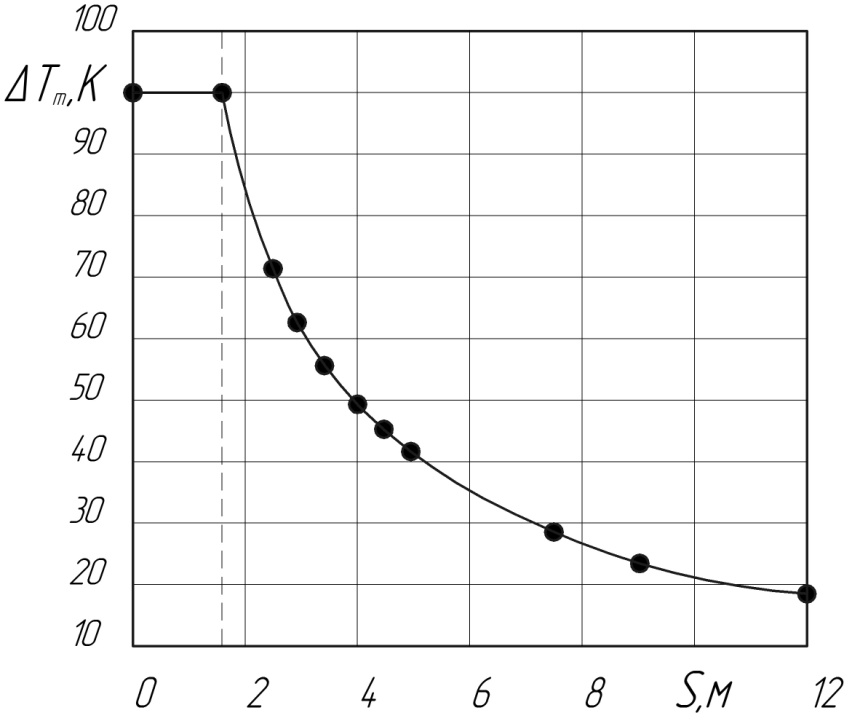
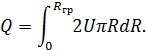
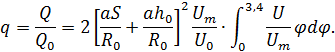
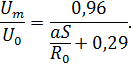
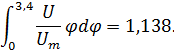
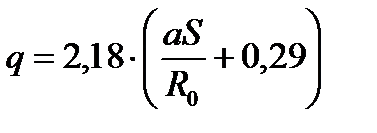 . (37)
. (37)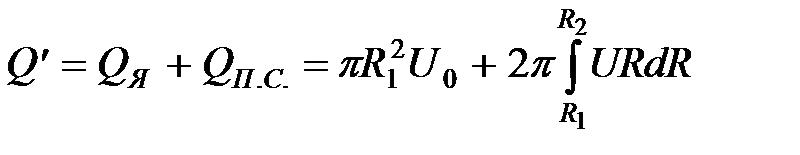 ,
,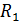 - радиус ядра постоянных скоростей,
- радиус ядра постоянных скоростей, 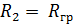 - радиус внешней границы пограничного слоя. Если выразим расход
- радиус внешней границы пограничного слоя. Если выразим расход 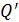 в долях от начального расхода
в долях от начального расхода 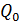 , то получим:
, то получим: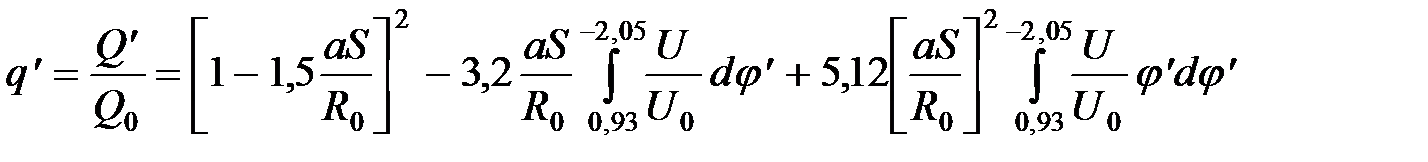 .
.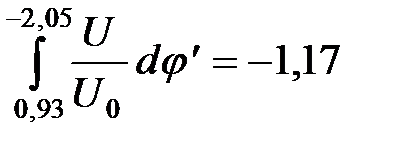 ;
; 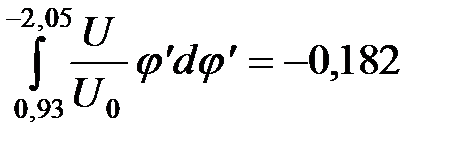 .
.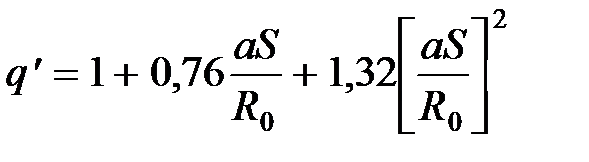 . (38)
. (38)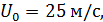
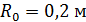 . Рассчитаем значение безразмерного расхода на начальном участке струи, при различных значениях
. Рассчитаем значение безразмерного расхода на начальном участке струи, при различных значениях 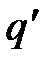
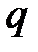
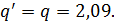
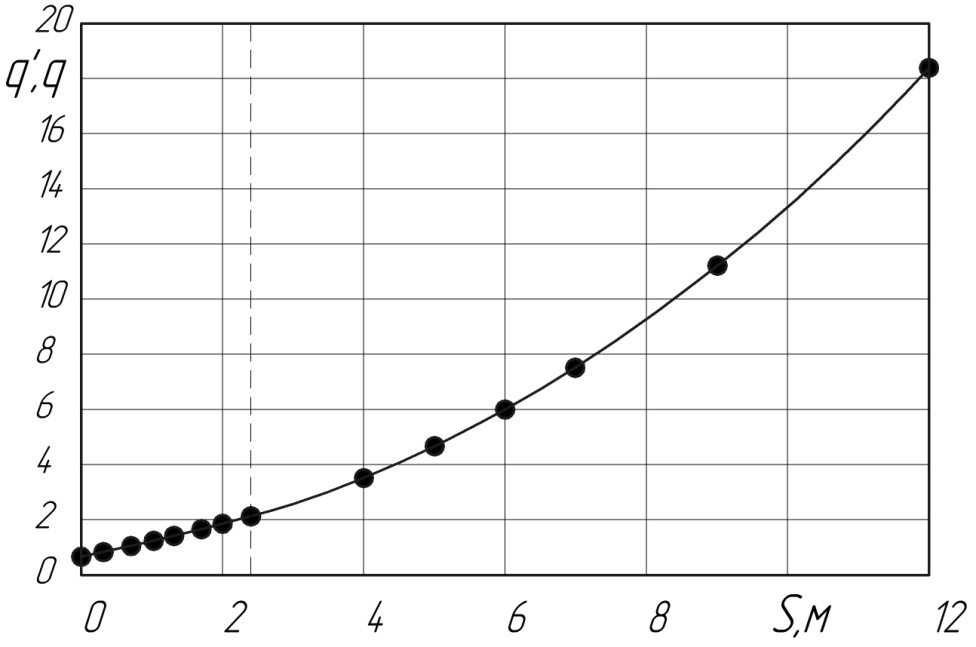
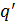 - безразмерный расход на начальном участке струи;
- безразмерный расход на начальном участке струи;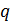 - безразмерный расход на основном участке струи.
- безразмерный расход на основном участке струи.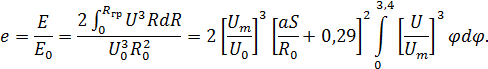
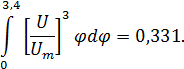
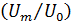 определяется выражением:
определяется выражением: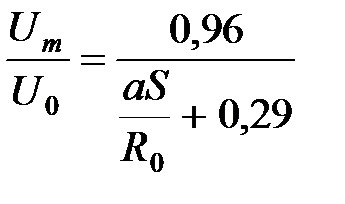 .
. 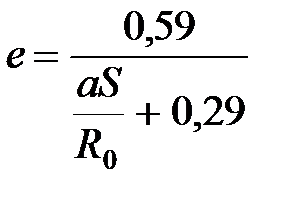 . (39)
. (39)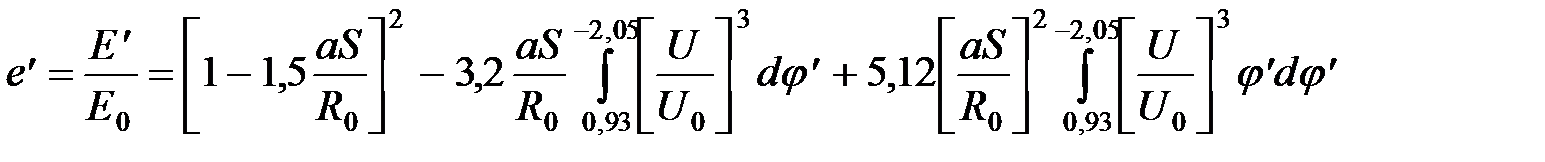 .
.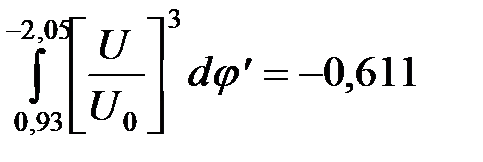 ;
; 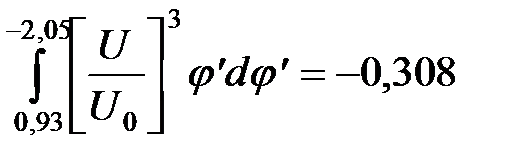 .
.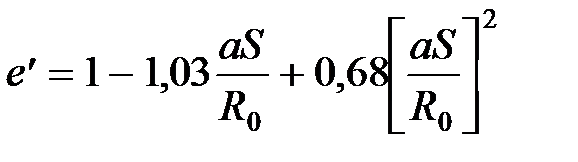 . (40)
. (40)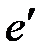
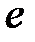
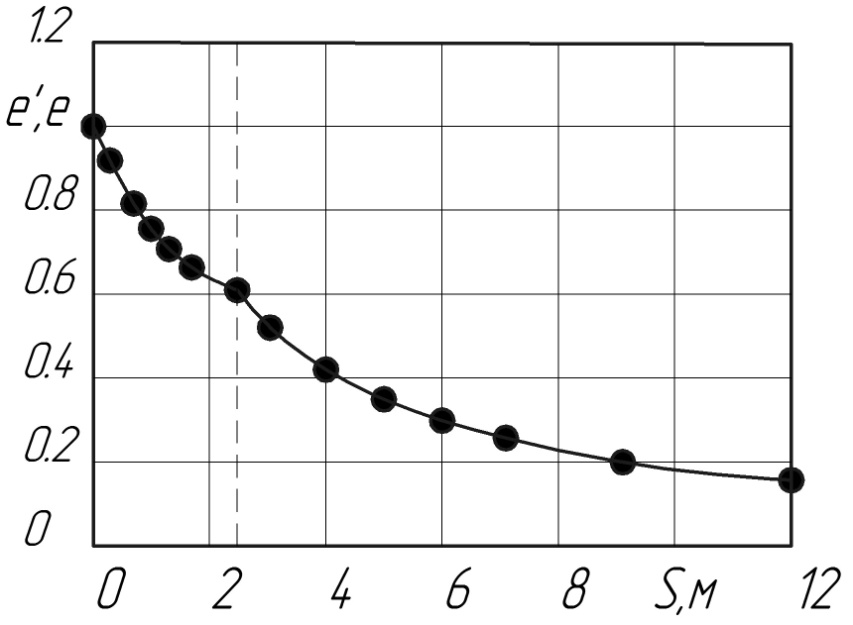
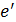 - безразмерный запас энергии на начальном участке струи;
- безразмерный запас энергии на начальном участке струи;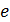 - безразмерный запас энергии на основном участке струи.
- безразмерный запас энергии на основном участке струи.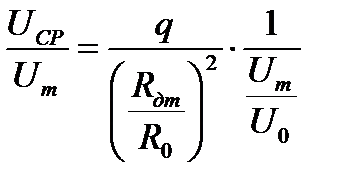 . (41)
. (41)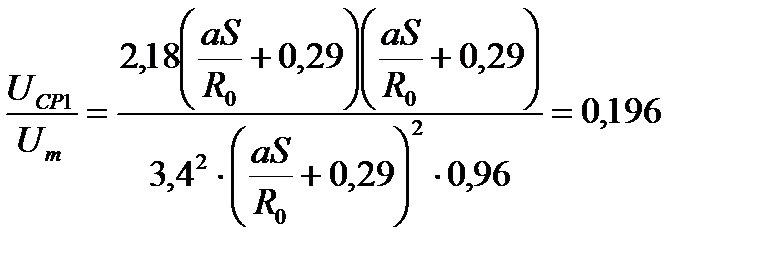 . (42)
. (42)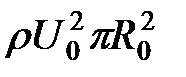 ,
,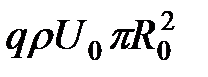 .
.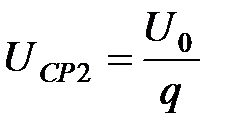 .
.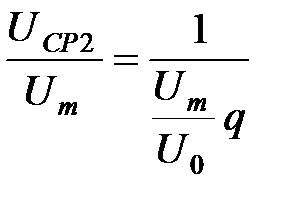 .
.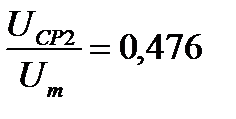 . (43)
. (43)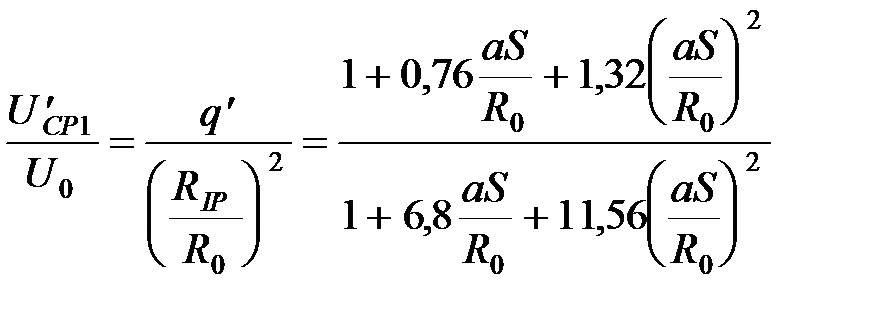 , (44)
, (44)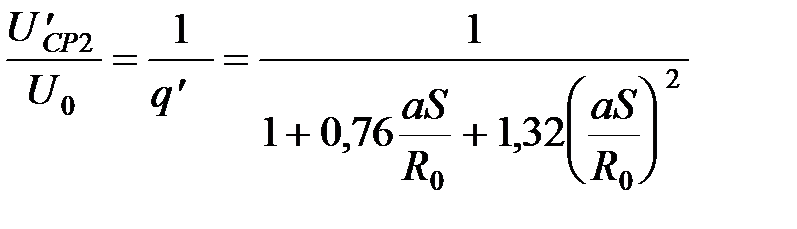 . (45)
. (45)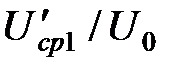
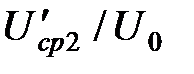
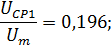
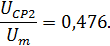
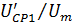 – безразмерная средняя арифметическая скорость на начальном участке;
– безразмерная средняя арифметическая скорость на начальном участке; 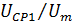 – безразмерная средняя арифметическая скорость на основном участке;
– безразмерная средняя арифметическая скорость на основном участке; 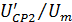 – безразмерная средняя квадратичная скорость на начальном участке;
– безразмерная средняя квадратичная скорость на начальном участке; 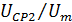 – безразмерная средняя квадратичная скорость на основном участке.
– безразмерная средняя квадратичная скорость на основном участке.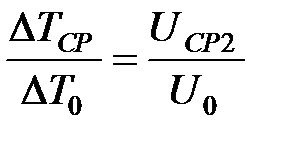 .
.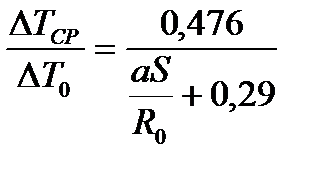 ; (46)
; (46)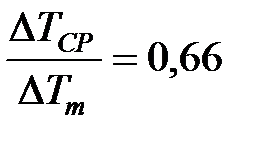 . (47)
. (47)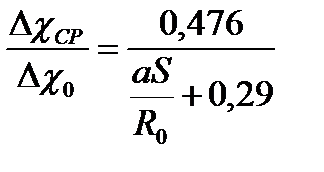 , (48)
, (48)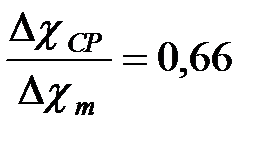 , (49)
, (49)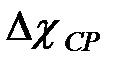 - средняя избыточная концентрация примесей в поперечном сечении струи;
- средняя избыточная концентрация примесей в поперечном сечении струи; 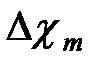 и
и 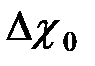 - значения избыточных концентраций соответственно на оси данного сечения и в начальном сечении.
- значения избыточных концентраций соответственно на оси данного сечения и в начальном сечении.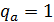 ).
).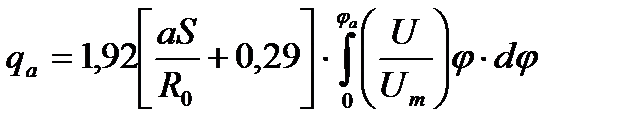 .
.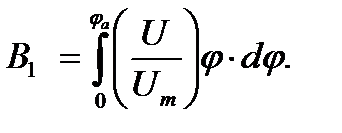
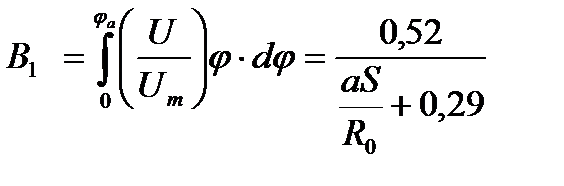 . (50)
. (50)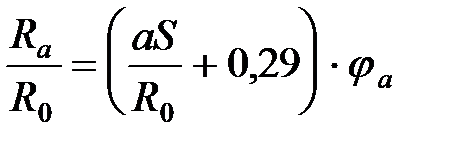 . (51)
. (51)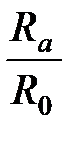 происходит по следующему принципу:
происходит по следующему принципу: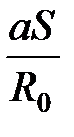 определяют величину В1.
определяют величину В1.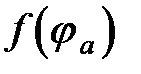 отыскивают соответствующие значения
отыскивают соответствующие значения 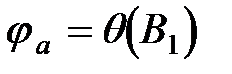 .
.
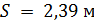 :
: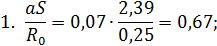
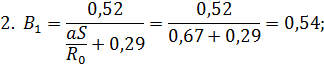
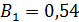 находим
находим 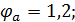

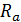 для основного участка струи:
для основного участка струи: