Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Описание методов вычислительной математики, используемых при решенииСтр 1 из 2Следующая ⇒ Содержание Нормативные ссылки……………………………………………………………………5 Введение……………………………………………………………………………….....6 3 Специфика задачи …………………………………………………………………...7 4 Формулировка задачи………………………………………………………………..8 5 Описание методов вычислительной математики……………………………………9 6 Описание методов программирования ……………………………………………....11 7 Листинг программы …………………………………………………………………13 8 Описание программы …………………………………………………...………….....15 9Тестирование программы…………………………………………………...………...17 10 Заключение………………………………………………………………....................18 Список используемых источников……………………………………………………..19
Нормативные ссылки
ГОСТ Р 1.5-2002 ГСС РФ. Стандарты. Общие требования к построению, изложению, оформлению, содержанию и обозначению ГОСТ 2.301-68 ЕСКД. Форматы ГОСТ 7.1-2003 СИБИД. Библиографическая запись. Библиографическое описание. Общие требования и правила составления ГОСТ 7.12-93 СИБИД. Библиографическая запись. Сокращения слов на русском языке. Общие требования и правила ГОСТ 7.9-95 СИБИД. Реферат и аннотация. Общие требования ГОСТ 7.82-2001 СИБИД. Библиографическая запись. Библиографическое описание электронных ресурсов. Общие требования и правила составления
Введение В современном мире разработка программ играет важную роль. Они помогают быстро справиться с решением многих важных задач. Для этого можно воспользоваться средствами вычислительной техники – составить программу на языке программирования.  В данной курсовой работе рассматривается возможность перевода чисел с 10 системы счисления в 8, созданной на языке программирования VBA. Язык программирования VBA на сегодняшний день является одним из лучших средств разработки приложений предназначенных для упрощения работы в пакете Microsoft Office. Данные продукты позволяют разрабатывать как консольные приложения, так и приложения с графическим интерфейсом, в том числе с поддержкой технологий UserForms.
Специфика задачи Разрабатываемая программа должна обладать следующими качествами: · Производить перевод десятичного числа в восьмеричную систему счисления.
Формулировка задачи Данная курсовая работа посвящена разработке программы на языке VBA, которая переводит число в другую систему счисления. Задача курсового проекта – разработать программу на языке VBA, такую, чтобы при работе с этой программой пользователь имел возможность: · Перевести введенное им десятичное число в восьмеричную систему счисления.
Описание методов вычислительной математики, используемых при решении Пусть X - число в системе счисления с основанием s, которое требуется представить в системе с основанием h. Удобно различать два случая. В первом случае
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10. Во втором случае ( Перевод целых чисел Правила перевода целых чисел становится ясным из общей формулы записи числа в произвольной позиционной системе. Пусть число
Для нахождения значений
Как видно, младший разряд
Остальные Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению. Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы. Решение:
Перевод правильных дробей Правильную дробь
Старшая цифра
Если это произведение меньше 1, то цифра Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам "старой" s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления. Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления. * В двоичную систему:
Ответ: ** В восьмеричную систему:
Ответ: *** В шестнадцатеричную систему:
Блок-схемы программы.
Листинг программы Function dec_in_oct(ByVal dec As Long, s As Integer) As String
Dim alpha As String, str As String
alpha = "01234567"
If dec < 0 Then MsgBox ("Введено отрицательное число") Exit Function End If
Do str = Mid(alpha, (dec Mod s) + 1, 1) + str dec = dec \ s Loop While dec <> 0
dec_in_oct = str
End Function
Sub main() Dim a As Integer Dim b As String b = UserForm1.TextBox1.Value UserForm1.Label2.Visible = True UserForm1.Label2.Caption = dec_in_oct(CInt(b), 8) End Sub
Sub open_form() UserForm1.Show End Sub
Тестирование программы
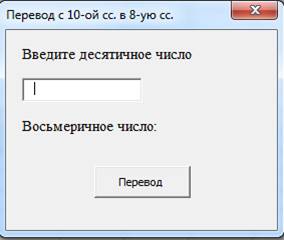
Пользователь запускает программу, в поле для ввода вводит десятичное число и нажимает кнопку «Перевод».
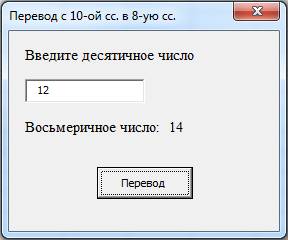
Результат работы. Пользователь ввел число 12 и программа перевела это число в восьмеричную систему счисления.
Заключение В результате выполнения курсовой работы разработана программа, согласно заданию. С помощью этой программы можно любое десятичное число в восьмеричную систему счисления. Данная программа в дальнейшем может быть развита как приложение Windows, которое будет позволять вводить данные в компоненты приложения.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 411. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
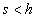 и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа
и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа 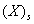 в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры: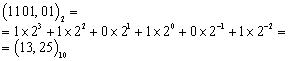 .
.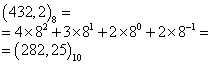 .
.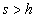 ) удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
) удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.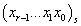 . Требуется получить запись числа в системе счисления с основанием h:
. Требуется получить запись числа в системе счисления с основанием h: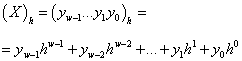 .
.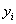 разделим этот многочлен на h:
разделим этот многочлен на h: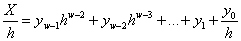 .
.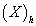 , то есть
, то есть 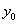 , равен первому остатку. Следующий значащий разряд
, равен первому остатку. Следующий значащий разряд 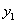 определяется делением частного
определяется делением частного 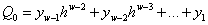 наh:
наh: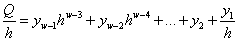 .
.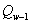 не станет равным нулю.
не станет равным нулю.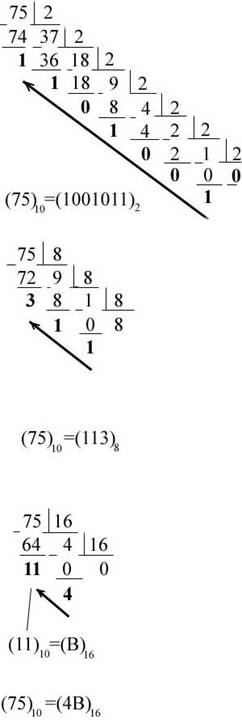
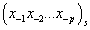 , можно выразить в системе счисления с основанием h как многочлен вида
, можно выразить в системе счисления с основанием h как многочлен вида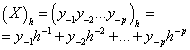
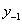 может быть найдена умножением этого многочлена на h, т.е.
может быть найдена умножением этого многочлена на h, т.е.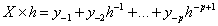
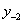 определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.
определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.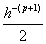 .
.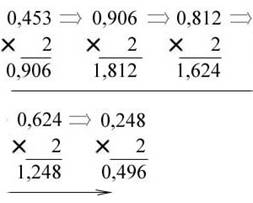
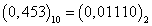
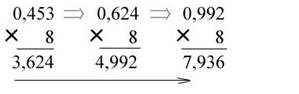
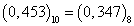

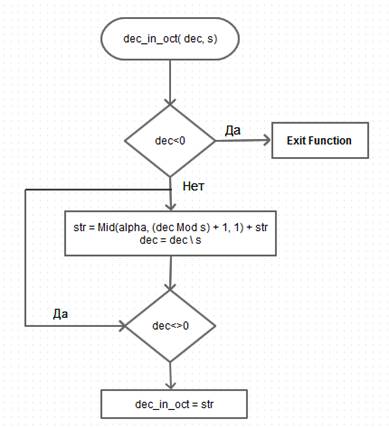 Блок-схема функции в которой происходит перевод в восьмеричную систему счисления.
Блок-схема функции в которой происходит перевод в восьмеричную систему счисления.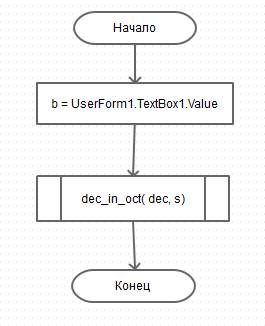 Блок-схема основного модуля программы.
Блок-схема основного модуля программы.