Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение оптимальных параметров нейросети в среде Matlab.Стр 1 из 3Следующая ⇒ Техническое задание Разработать алгоритм и программу на языке С# в соответствии с вариантом индивидуального задания. Исследовать метод обратного распространения ошибки для обучения нейросети. Введение
В данной курсовой работе необходимо разработать алгоритм и программу на языке С# вычислительного процесса (двухслойная нейросеть). В наши дни возрастает необходимость в системах, которые способны не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и способны сами анализировать вновь поступающую информацию, находить в ней закономерности, производить прогнозирование и т.д. В этой области приложений самым лучшим образом зарекомендовали себя так называемые нейронные сети – самообучающиеся системы, имитирующие деятельность человеческого мозга. Целью данной работы является исследование параметров обучения нейросети методом обратного распространения ошибки. А так же закрепление практических навыков программирования на С#. Процесс подготовки предусматривает самостоятельное изучение нового материала и закрепление его с помощью практического задания.
Разработка алгоритма Для дальнейшей работы необходимо построить следующие алгоритмы: алгоритм работы программы в целом, алгоритм обучения нейросети. Математический алгоритм
1.1.1. Нормальное распределение. Центра́льные преде́льные теоре́мы— класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.  Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения. Пусть Пусть Тогда где N(0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом Используя вышеприведенные формулы, формируем 4 класса чисел с нормальным распределением: 1 класс – μ=0; 2 класс – μ=5; 3 класс – μ=2,5; 4 класс – μ=10.
1.1.2. Искусственные нейронные сети. Несмотря на большое разнообразие вариантов нейронных сетей, все они имеют общие черты. Так, все они, так же, как и мозг человека, состоят из большого числа связанных между собой однотипных элементов – нейронов, которые имитируют нейроны головного мозга. На рис. 1 показана схема нейрона.
Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов, связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона, который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние.
где : n – число входов нейрона xi – значение i-го входа нейрона wi – вес i-го синапса Затем определяется значение аксона нейрона по формуле
Где f – некоторая функция, которая называется активационной. Наиболее часто в качестве активационной функции используется сигмоид, который имеет следующий вид:
Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:
При уменьшении параметра a сигмоид, становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при a=0. При увеличении a, сигмоид приближается к функции единичного скачка. Список других наиболее употребляемых функций активации приведен в таблице 1. Таблица 1- Основные функций активации.
Обучение нейронной сети Самым важным свойством нейронных сетей является их способность обучаться на основе данных окружающей среды и в результате обучения повышать свою производительность. Обучение нейронной сети происходит посредством интерактивного процесса корректировки синаптических весов и порогов. Существуют два концептуальных подхода к обучению нейронных сетей: обучение с учителем и обучение без учителя. В данной курсовой работе используется метод обучения с учителем. Обучение нейронной сети с учителем предполагает, что для каждого входного вектора из обучающего множества существует требуемое значение выходного вектора, называемого целевым. Эти вектора образуют обучающую пару. Веса сети изменяют до тех пор, пока для каждого входного вектора не будет получен приемлемый уровень отклонения выходного вектора от целевого. Алгоритм обратного распространения ошибки: 1. Инициализировать синаптические веса маленькими случайными значениями. 2. Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети. 3. Вычислить выход сети. 4. Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары). 5. Подкорректировать веса сети для минимизации ошибки (как см. ниже). Повторять шаги с 2 по 5 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня. Рассмотрим подробней 5 шаг – корректировка весов сети. Здесь следует выделить два нижеописанных случая. Случай 1. Корректировка синаптических весов выходного слоя Определимся, что индексом p будем обозначать нейрон, из которого выходит синаптический вес, а q – нейрон в который входит. Введем величину δ, которая равна разности между требуемым и реальным выходами, умноженной на производную функции активации: Тогда, веса выходного слоя после коррекции будут равны:
где: i – номер текущей итерации обучения;
Случай 2. Корректировка синаптических весов скрытого слоя.
где:
Тогда, веса скрытого слоя после коррекции будут равны:
В этом алгоритме происходит распространение ошибки от выходов НС ко входам, то есть в направлении обратном распространению сигналов обычном режиме работы. Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
где Чтобы определить оптимальные параметры обучения нейросети данным методом, такие как количество шагов обучения, скорость обучения и коэффициент сигмоида, мы будем анализировать величину ошибки (13). Для этого мы будем использовать среду Matlab. Мы должны сначала составить таблицы значений ошибки обучения, как функции от 3-х параметров: шага обучения, скорости обучения и коэффициента а в функции активации (7). План эксперимента: Коэффициент сигмоиды изменяется от 0 до 10 с шагом 0,1; Количество шагов обучения – 100; Так как поверхность является функцией от двух переменных, коэффициент скорости обучения должен быть константой. Поэтому его возьмем равным 3 конкретным значениям: 0,5; 1; 1,5. Тогда функция ошибки будет зависеть от двух параметров, и мы сможем построить ее график. Анализируя графики, мы сможем выбрать оптимальные значения этих параметров.
Разработка схем алгоритмов
Для дальнейшей работы необходимо построить следующие алгоритмы: алгоритм работы программы в целом, и алгоритм обучения нейросети. Обобщенная схема алгоритма программы, распознающей 2 класса чисел с помощью искусственной нейросети, представлена на рисунке 2.
Рисунок 3 - Обобщенная схема алгоритма программы, распознающей 2 класса чисел с помощью искусственной нейросети.
Алгоритм обучения нейросети представлен на рисунке 3.
Рисунок 4 – Схема алгоритма обучения нейросети
Разработка программы
Разработанная программа предназначена для выполнения курсового проекта, а также демонстрирует изученные в процессе обучения навыки владения языком C#. Для запуска этой программы необходимо иметь на компьютере установленную версию Windows XP/Vista/7. Данная программа разрабатывалась в среде MSVisualC# 2010(Microsoft .NET Framework 4.0). Для работы использовались следующие пространства имен: System; System.Collections.Generic; System.ComponentModel; System.Data; System.Drawing; System.Text; System.Windows.Forms; System.Threading; System.IO;
Для создания программы были использованы: class Neyro – класс работающий с нейросетью. class Form1 : Form – класс диалогового окна, наследуемый от стандартного класса Form. public int[] Vihod(int kol, int kl) - метод, формирующий целевой вектор. public void Korekt() - метод, коректирующий синапсы. public void Rez() – метод вычисления результата нейросети. public void CreateNS() – метод, создающий нейросеть. public void Obuchenie(string file, StreamWriter sw1) – метод, обучающий нейросеть определенному классу чисел. private void grafic() – метод, рисующий график. Текст программы представлен в приложении А.
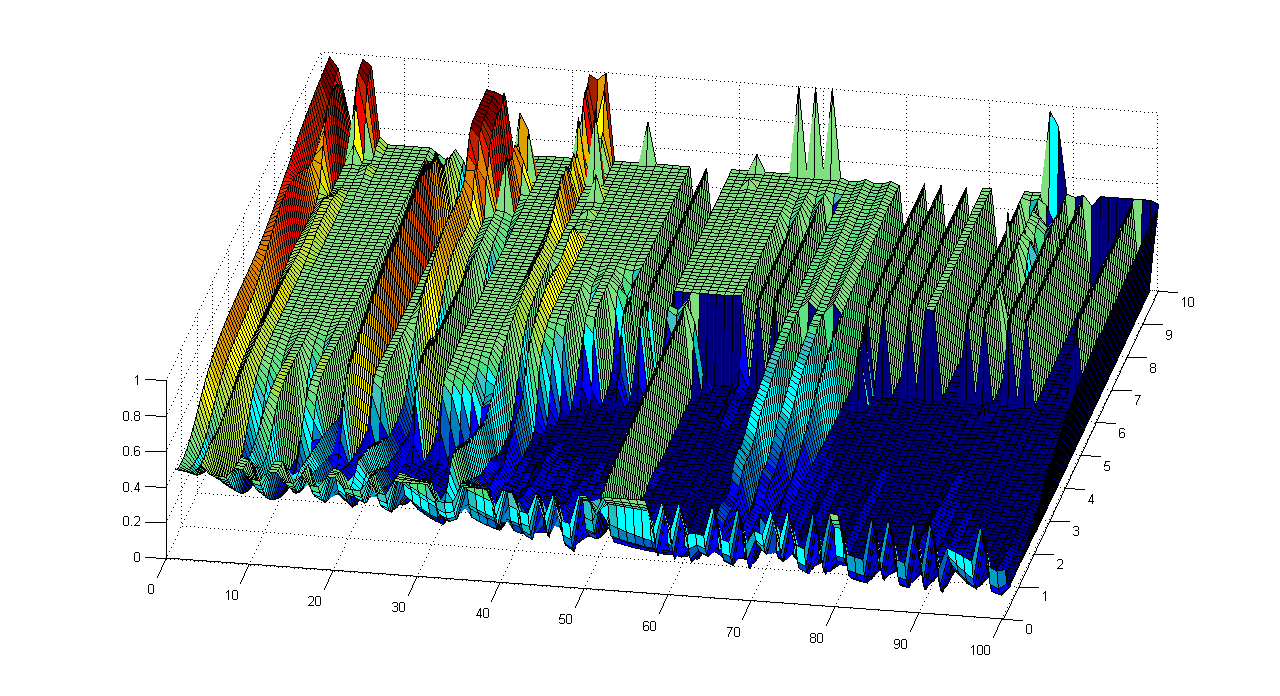
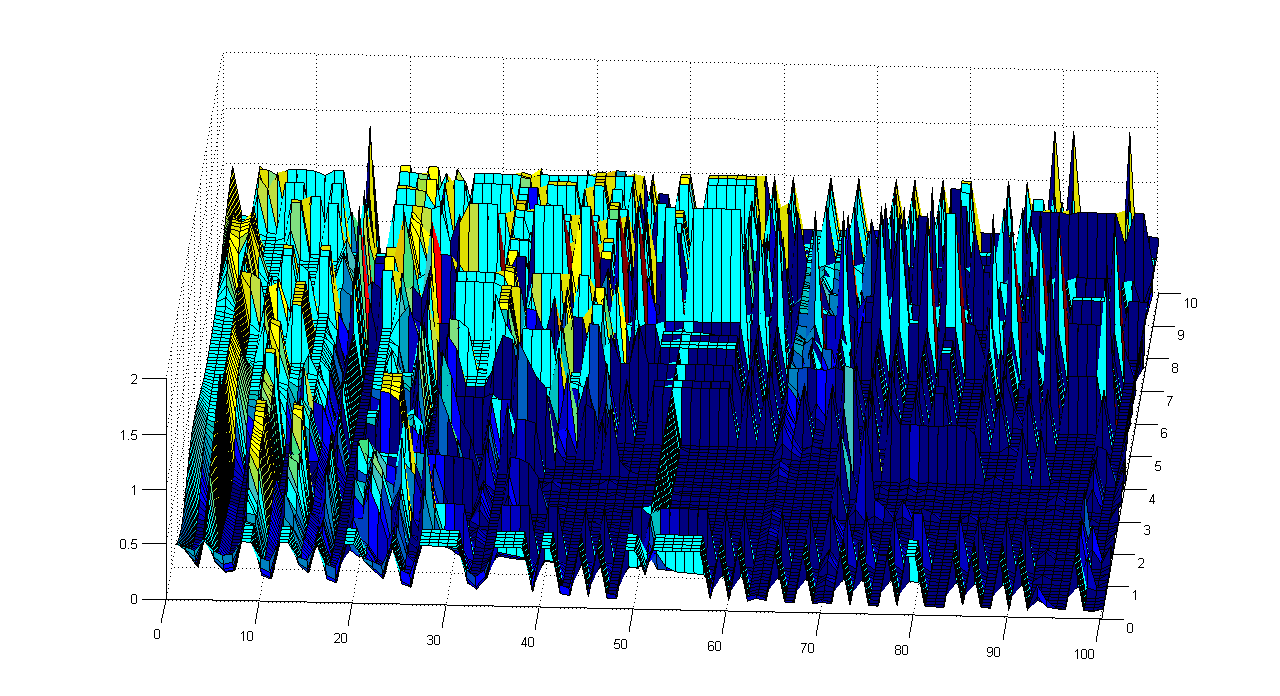
Вычислительный эксперимент Определение оптимальных параметров нейросети в среде Matlab. После выполнения программы появляются три графика. Результаты представлены на рисунках 4,5,6.
Рисунок 5 – График ошибки при значении коэффициента скорости обучения 0,5.
Рисунок 6 – График ошибки при значении коэффициента скорости обучения 1.
Рисунок 7 – График ошибки при значении коэффициента скорости обучения 1,5. Анализируя полученные результаты, можно сделать вывод, что для эффективной работы нейросети, коэффициент скорости обучения должен принимать значения от 0,5 до 1. Коэффициент а в функции активации (7) нужно выбирать в пределах от 2 до 4. Количество шагов обучения лучше оставить равным 100. Конкретные значения нужно будет подобрать экспериментально, в зависимости от процента правильного распознавания при тех или иных значениях коэффициентов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 574. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
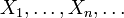 есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожиданием и дисперсию. Обозначим последние μ и σ2, соответственно.
есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожиданием и дисперсию. Обозначим последние μ и σ2, соответственно.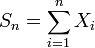 (1)
(1)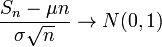 по распределению при
по распределению при  , (2)
, (2) выборочное среднее первых n величин, то есть
выборочное среднее первых n величин, то есть  (3), мы можем переписать результат центральной предельной теоремы в следующем виде:
(3), мы можем переписать результат центральной предельной теоремы в следующем виде:  по распределению при
по распределению при 

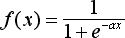
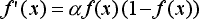
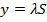





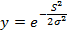
 [-1,1])
[-1,1])

 (9)
(9) (10)
(10) – величина синаптического веса, соединяющего нейрон p с нейроном q;
– величина синаптического веса, соединяющего нейрон p с нейроном q; – коэффициент «скорости обучения», позволяет управлять средней величиной изменения весов;
– коэффициент «скорости обучения», позволяет управлять средней величиной изменения весов; – выход нейрона .
– выход нейрона . (11)
(11) – сумма от 1 по N, N – количество нейронов выходного слоя.
– сумма от 1 по N, N – количество нейронов выходного слоя. (13)
(13) реальное выходное состояние нейрона
реальное выходное состояние нейрона  выходного слоя N нейронной сети при подаче на ее входы
выходного слоя N нейронной сети при подаче на ее входы  - го образа;
- го образа;  - желаемое (идеальное) выходное состояние этого нейрона. Суммирование происходит по всем нейронам выходного слоя и по всем обрабатываемым сетью образам.
- желаемое (идеальное) выходное состояние этого нейрона. Суммирование происходит по всем нейронам выходного слоя и по всем обрабатываемым сетью образам.